Misplaced Pages

Hydraulic jump in a rectangular channel, also known as classical jump, is a natural phenomenon that occurs whenever flow changes from supercritical to subcritical flow. In this transition, the water surface rises abruptly, surface rollers are formed, intense mixing occurs, air is entrained, and often a large amount of energy is dissipated. Numeric models created using the standard step method or HEC-RAS are used to track supercritical and subcritical flows to determine where in a specific reach a hydraulic jump will form.

There are common hydraulic jumps that occur in everyday situations such as during the use of a household sink. There are also man-made hydraulic jumps created by devices like weirs or sluice gates. In general, a hydraulic jump may be used to dissipate energy, to mix chemicals, or to act as an aeration device.

To produce equations describing the jump, since there is an unknown energy loss, there is a need to apply conservation of momentum. To develop this equation, a general situation in which there may or may not be an energy loss between upstream and downstream, and there may or may not be some obstacle on which there is a drag force P_f is considered. however, for a simple or classic hydraulic jump the force per unit width(P_f) equals 0. From there the momentum equation, and the conjugate depths equation can be derived.

About hydraulic jumps

The depth of supercritical flow, y₁, ‘jumps’ up to its subcritical conjugate depth, y₂, and the result of this abrupt change in flow conditions is considerable turbulence and Energy Loss, E_L. Figure 1 shows a schematic of typical jump characteristics where E₁ is the energy of the upstream flow, E₂ is the energy of the downstream flow and L_j is the length of the hydraulic jump. A series of small surface rollers are formed in a standing wave like the one shown in Figure 1.

Figure 1. Hydraulic Jump Overall Schematic

Common hydraulic jumps

Hydraulic jumps occur commonly in everyday situations such as during the use of any household sink. The jump can be seen in the form of a circular, stationary wave surrounding the inflow of water. The hydraulic jump occurs at the point where the seemingly still water becomes turbulent. As water hits the sink, it disperses, increasing in depth to a critical radius where the flow (supercritical with low depth, high velocity, and a Froude number greater than 1) must suddenly jump to a greater, subcritical depth (high depth, low velocity, and a Froude number less than 1) that is known to conserve momentum.

Figure 2. Turbulent hydraulic jump can be created in sink (left), viscous hydraulic jump can create advanced shapes (right) (Images courtesy of John Bush, MIT)

Man-made hydraulic jumps

Hydraulic jumps may also be manmade; as seen in Figure 2, scientists have been experimenting with the effects of viscosity on the hydraulic jump and have been able to create steady asymmetrical forms. In more practical applications, jumps are created in the environment with specific purposes such as erosion prevention. Erosion in stream beds is often caused by a high velocity water flow which leads to sediment transport. This process can be prevented by decreasing the velocity of the flow into the stream bed with the introduction of a hydraulic jump. Often in these cases, a hydraulic jump is created by devices such as a weir or sluice gate where the turbulent flow enters the stream. The mixture of chemical constituents in a solution is another practical use for hydraulic jumps. Introducing a hydraulic jump rapidly increases the turbulence of the flow, allowing sufficient constituent mixing without the use of any additional mechanisms. The wastewater industry sometimes uses hydraulic jumps as a way to mix solutions, minimizing the need to implement more expensive mechanical mixing systems.

Figure 3. Weir in Riverfront Park, WA (left) and Hydraulic Jump in Coagulation Chamber (right)

Still another use for manmade hydraulic jumps is energy dissipation. One example of an energy dissipating use is a hydraulic jump stilling basin. In these basins, horizontal and sloping aprons are used to dissipate up to 60% of the energy of incoming flow; the basins implement devices such as chute blocks, baffle piers, and dentated ends whose effectiveness in energy dissipation is dependent on the Froude number of the incoming flow. ‘Hydraulic jump stilling basins are not typically suggested for use when dealing with heads greater than 100 meters due to complications caused by turbulences like intermittent cavitation, vibration, uplift, and hydrodynamic loading.’ Other hydraulic structures such as dams and weirs also use these same energy dissipating principles to reduce the incoming force from turbulent flows that tend to scour or erode downstream areas.

Figure 4. Stilling Basin On Oker River in the Harz-Mointains at Opened Scour Outlet (left) and Stilling Basin for Griggs Dam in Columbus, OH (right)

Derivation of formula for simple, momentum conserving hydraulic jump in rectangular channel

Definitions of momentum

Momentum is defined as the product of mass times velocity, and like velocity, it is a vector. French Scientist and Philosopher of the early 1600s René Descartes first discovered the concept of momentum but got stuck on the amount of motion (speed) which was not being conserved. Christiaan Huygens, a Dutch Scientist, pointed out that the "quantity of motion" did not need to be a positive value; a negative value meant that it was moving in the opposite direction.

Definition of variables

mv = momentum = mass x velocity MLT

ρ = density ML

q = Q''/w = flow rate per unit width LT

F_d = dynamic force due to frictional resistance MLT

P₁ = upstream pressure MLT

P₂ = downstream pressure force MLT

y₁ = upstream depth L

y₂ = downstream depth L

F_r = Froude number LT

h_j = height of hydraulic jump L

M = momentum function (specific force + momentum) L

γ = specific weight of water (9810 N/m) MLT

The basic principles behind the momentum function are:

1. Conservation of momentum which "states that the total momentum of a closed system of objects (which has no interactions with external agents) is constant" and
2. Newton's laws of motion stating that the sum of the forces in a particular direction is equal to the mass times acceleration in that direction.

This section may be confusing or unclear to readers. Please help clarify the section. There might be a discussion about this on the talk page. (October 2013) (Learn how and when to remove this message)

${\displaystyle \sum F_{x}=\Delta (ma_{x})}$

${\displaystyle \sum F=\Delta m\times {\frac {dy}{dt}}}$ = change in mass × change in velocity

momentum = mv

${\displaystyle \Delta mv=\Delta m\times {\frac {dy}{dt}}}$ = change in mass × change in velocity

${\displaystyle \sum F_{x}=\Delta (mv_{x})}$

The following derivation is for the momentum function of a simple momentum conserving hydraulic jump in a rectangular channel with constant width.

1. Change in momentum.
       ${\displaystyle \Delta (mv)(w)=\rho (Q)(v_{2}-v_{1})}$
2. Divide through by w to obtain q. Change in momentum per unit width.
       ${\displaystyle \Delta (mv)=\rho q(v_{2}-v_{1})}$
3. Sum of forces in the direction of flow.
   ${\displaystyle \sum F=P_{1}-P_{2}-F_{d}\qquad {\text{where }}P={\gamma \times y^{2} \over 2}}$
4. The sum of forces is equal to the momentum change.
       ${\displaystyle {\gamma \times y_{1}^{2} \over 2}-{\gamma \times y_{2}^{2} \over 2}-F_{d}=\rho q(v_{2}-v_{1})}$
5. Divide by γ.
     ${\displaystyle {y_{1}^{2} \over 2}-{y_{2}^{2} \over 2}-{F_{d} \over \gamma }={\rho \times q\times (v_{2}-v_{1}) \over \gamma }}$
6. Recall that ${\displaystyle {\frac {1}{g}}={\rho \over \gamma }}$
     ${\displaystyle {y_{1}^{2} \over 2}+{qv_{1} \over g}={y_{2}^{2} \over 2}+{qv_{2} \over g}}$
7. Recall that ${\displaystyle v={\frac {q}{y}}}$ to obtain the equation for M.
     ${\displaystyle M={y_{1}^{2} \over 2}+{q^{2} \over gy_{1}}={y_{2}^{2} \over 2}+{q^{2} \over gy_{2}}}$

Conjugate depths relationships

Conjugate depths are the depths (y₁) upstream and the depth (y₂) downstream of the hydraulic jump whose momentum functions are equal for a given unit discharge, q. The depth upstream of a hydraulic jump is always supercritical, and the depth downstream of a hydraulic jump is always subcritical. It is important to note that the conjugate depth is different than the alternate depths for flow which are used in energy conservation calculations.

Mathematical derivation of equation

(1) Beginning with momentum function, we equate momentum between locations 1 and 2:

${\displaystyle M={\frac {y_{1}^{2}}{2}}+{\frac {q^{2}}{gy_{1}}}={\frac {y_{2}^{2}}{2}}+{\frac {q^{2}}{gy_{2}}}}$

(2) Rearranging terms by moving the q terms to the left and the 1/2 terms to the right, we get:

${\displaystyle {\frac {q^{2}}{g}}\left({\frac {1}{y_{1}}}-{\frac {1}{y_{2}}}\right)={\frac {1}{2}}\left(y_{2}^{2}-y_{1}^{2}\right)}$

(3) We then multiply to get a common denominator on the left-hand side and factor the right-hand side:

${\displaystyle {\frac {q^{2}}{g}}\left({\frac {y_{2}-y_{1}}{y_{1}y_{2}}}\right)={\frac {1}{2}}(y_{2}-y_{1})(y_{2}+y_{1})}$

(4) The (y₂−y₁) term cancels out:

${\displaystyle {\frac {q^{2}}{g}}\left({\frac {1}{y_{1}y_{2}}}\right)={\frac {1}{2}}(y_{2}+y_{1})\qquad {\text{where }}q_{1}^{2}=y_{1}^{2}v_{1}^{2}=y_{2}^{2}v_{2}^{2}}$

(5) Divide by y₁

${\displaystyle {\frac {v_{1}^{2}}{g}}\left({\frac {1}{y_{1}y_{2}}}\right)={\frac {1}{2y_{1}^{2}}}(y_{2}+y_{1})\qquad {\text{recall }}Fr_{1}^{2}={\frac {v_{1}^{2}}{gy_{1}}}}$

(6) Multiply by y₂ and expand right-hand side:

${\displaystyle Fr_{1}^{2}={\frac {y_{2}^{2}}{2y_{1}^{2}}}+{\frac {y_{2}}{2y_{1}}}}$

(7) Substitute x for the quantity y₂/y₁. We have a quadratic equation in x:

${\displaystyle Fr_{1}^{2}={\frac {x^{2}}{2}}+{\frac {x}{2}}}$

${\displaystyle \Rightarrow 0={\frac {x^{2}}{2}}+{\frac {x}{2}}-Fr_{1}^{2}\qquad \Rightarrow 0=x^{2}+x-2Fr_{1}^{2}\qquad a=1,\;b=1,\;c=-2Fr_{1}^{2}}$

(8) Using the quadratic equation:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$

${\displaystyle x={\frac {-1\pm {\sqrt {(1^{2})-4(1)(-2Fr_{1}^{2})}}}{2(1)}}={\frac {-1\pm {\sqrt {1+8Fr_{1}^{2}}}}{2}}}$

Since:

${\displaystyle {\sqrt {1+8Fr_{1}^{2}}}}$ must be positive,

${\displaystyle x={\frac {-1-{\sqrt {1+8Fr_{1}^{2}}}}{2}}}$ produces a negative number.

This is not possible because x represents a ratio of positive depths ${\displaystyle {\frac {y_{2}}{y_{1}}}}$.

(9) Hence, substituting the constant y₂/y₁ back in for x to get the conjugate depth equation:

${\displaystyle x={\frac {-1+{\sqrt {1+8Fr_{1}^{2}}}}{2}}}$

${\displaystyle x={\frac {y_{2}}{y_{1}}}={\frac {1}{2}}\left({\sqrt {1+8Fr_{1}^{2}}}-1\right)}$

Relationship of conjugate depths on M-y diagram

Example 1: Conjugate depths and the M-y diagram

Given:

Rectangular channel

Flow per unit width, q = 10 ft/s

Depth, y₁ = 0.24 ft

Find:

M-y Diagram and depth after the hydraulic jump

Solution:

For depth after hydraulic jump, y₂:

${\displaystyle (1)\quad y_{2}={\frac {y_{1}}{2}}\left({\sqrt {1+8Fr_{1}^{2}}}-1\right)}$

${\displaystyle (2)\quad Fr_{1}={\frac {v}{(gy_{1})^{1/2}}}={\frac {q}{y_{1}(gy_{1})^{1/2}}}}$

${\displaystyle (3)\quad Fr_{1}^{2}={\frac {q^{2}}{gy_{1}^{3}}}={\frac {(10)^{2}}{32.2*(0.24^{3})}}=224.65}$

${\displaystyle (4)\quad y_{2}={\frac {0.24}{2}}{\sqrt {1+8(224.65)}}-1=4.97\;ft}$

${\displaystyle (5)\quad M_{1}={\frac {(0.24)^{2}}{2}}+{\frac {q^{2}}{g*(0.24)}}=13\;ft^{2}}$

${\displaystyle (6)\quad M_{2}={\frac {(4.97)^{2}}{2}}+{\frac {q^{2}}{g*(4.97)}}=13\;ft^{2}}$

The M-y Diagram for this example is plotted below. To develop the M-y Diagram, we plot the value of M as a function of depth with M on the x-axis and depth on the y-axis since this is more naturally conducive to visualizing the change in momentum with depth. This example is a very basic hydraulic jump situation where the flow approaches at a supercritical depth, y₁, and jumps to its subcritical conjugate depth, y₂, in order to obtain the necessary energy to continue moving down the channel with the given flow rate, q.

Figure 6. M-y Diagram

Explanation of diagram and what it represents

The M-y Diagram is a graphical representation of the conservation of momentum and can be applied over a hydraulic jump to find the upstream and downstream depths. We can see from the above example that the flow approaches supercritically at a depth of y₁. There is a jump to the subcritical conjugate depth of y₁ which is labeled as y₂ in Figure 6. Figure 6 helps in visualizing how two depths can exist with the same momentum.

Analysis of important M-y curve locations

There are a few key locations on the M-y diagram which are labeled in Figure 6 above developed based on the information in Example 1. The first location of interest is the critical point labeled with y_c and M_c in Figure 6. The critical point represents the minimum value of the momentum function available for that particular flow per unit width, q. An increase in q would cause the M function to move to the right and slightly up, giving the flow access to more momentum at its critical point. It follows that a decrease in the q value would move the M function down and to the left, decreasing the momentum available to the flow at its critical value. This is shown graphically Figure 7 below.

Figure 7. Effect of increasing q on depth up- and down-stream of hydraulic jump

From Figure 7, it can also be seen what effect increasing the flow rate, q, will have on the depth up- and down-stream of the jump. Increasing the incoming flow rate (from q = 10 ft/s to 30 ft/s in Figure 7) will result in an increase in the supercritical approach depth and a decrease in the subcritical depth post-jump. This can be seen in Figure 6 by the decrease in depth from y_1,q=30 to y_1,q=10 and the increase in depth between y_2,q=30 and y_2,q=10. From this analysis of the change in depth due to a change in flow rate, we can also imagine that the energy lost in a jump with a value of q = 10 ft/s would be different from that of a jump with q = 30 ft/s. This is further discussed in Section 5.1.

Calculations for typical parameters in simple hydraulic jumps in rectangular channels

Energy loss

Although momentum is conserved throughout the hydraulic jump, the energy is not. There is an initial loss of energy when the flow jumps from supercritical to subcritical depths. The resulting loss of energy is equal to the change in specific energy across the jump and is given by the equation for ΔE below. The equation below is based on the condition that y₁ and y₂ are conjugate depths.

${\displaystyle \Delta E=E_{1}-E_{2}=\left(y_{1}+{\frac {q^{2}}{2gy_{1}^{2}}}\right)-\left(y_{2}+{\frac {q^{2}}{2gy_{2}^{2}}}\right)={\frac {(y_{2}-y_{1})^{3}}{4y_{1}y_{2}}}}$

When looking at the critical points on the M-y diagram and what their locations tell us about the nature of the hydraulic jump, we mentioned that an increase in q would affect the energy lost in the jump. From Figure 7 we see that increasing the flow rate decreases the difference in the upstream and downstream depth of the jump (y₂ – y₁). From this we can infer that if the momentum is held to be constant, there will be a decrease in the energy lost in the jump if the flow rate is increased.

The efficiency of the jump is determined by the dimensionless parameter E₂/E₁ which tells us how much of the original energy is remaining after the jump is complete. The equation for the energy efficiency is given below and shows the heavy dependence that the efficiency has on the Froude number of the upstream flow. Example 2 shows a sample calculation for energy loss and efficiency.

${\displaystyle {E_{2} \over E_{1}}={(8Fr_{1}^{2}+1)^{3/2}-4Fr_{1}^{2}+1 \over 8Fr_{1}^{2}(2+Fr_{1}^{2})}}$

Example 2: Energy loss and efficiency

Given:

Rectangular Channel

Velocity, v = 10 m/s

Depth, y₁ = 0.5 m

Find:

Energy loss and efficiency across the hydraulic jump

Solution:

${\displaystyle (1)\;Fr_{1}={\frac {v}{\sqrt {gy}}}={\frac {10}{\sqrt {9.81*0.5}}}=4.5}$

${\displaystyle (2)\;Fr_{1}>1\quad {\text{(supercritical flow)}}}$

${\displaystyle (3)\;y_{2}={\frac {y_{1}}{2}}\left({\sqrt {1+8Fr_{1}^{2}}}-1\right)={\frac {0.5}{2}}\left({\sqrt {1+8*4.5^{2}}}-1\right)=2.94\;m}$

${\displaystyle (4)\;\Delta E={\frac {(y_{2}-y_{1})^{3}}{4y_{1}y_{2}}}={\frac {(2.94-0.5)^{3}}{4*2.94*0.5}}=2.47\;m}$

${\displaystyle (5)\;{\frac {E_{2}}{E_{1}}}={\frac {(8Fr_{1}^{2}+1)^{3/2}-4Fr_{1}^{2}+1}{8Fr_{1}^{2}(2+F_{1}^{2})}}={\frac {(8*4.5^{2}+1)^{3/2}-4*4.5^{2}+1}{8*4.5^{2}(2+4.5^{2})}}=0.55}$

${\displaystyle (6)\;\%{\text{ efficiency}}=0.55*100=55\%{\text{ efficient}}\,}$

Length of hydraulic jump

Length of a hydraulic jump is often hard to measure in the field and during laboratory investigations due to the sudden changes in surface turbulence, in addition to the formation of roller and eddies. The length of a hydraulic jump is often an important factor to know when considering the design of structures like settling basins.

The equation derived for length is based on experimental data, and relates the length to the upstream Froude number.

${\displaystyle (1)\;L=220\times y_{1}\times \tanh {\frac {Fr_{1}-1}{22}}}$

Example 3: Length calculation

Given:

Use data from Example 2

Find:

Length of jump

Solution:

${\displaystyle (2)\;L=220*0.5*\tanh \left({\frac {4.5-1}{24}}\right)}$

${\displaystyle (3)\;\tanh(z)={\frac {e^{z}-e^{-z}}{e^{z}+e^{-z}}}\qquad {\text{if necessary, this is an alternate way to calculate }}\tanh(z)}$

${\displaystyle (4)\;z={\frac {4.5-1}{22}}=0.1591}$

${\displaystyle (5)\;\tanh(z)=0.1578}$

${\displaystyle (6)\;L=220*0.5*0.1578=17.4\;m}$

Height of hydraulic jump

The height of the hydraulic jump, similar to length, is useful to know when designing waterway structures like settling basins or spillways. The height of the hydraulic jump is simply the difference in flow depths prior to and after the hydraulic jump. The height can be determined using the Froude number and upstream energy.

Equations:

${\displaystyle (1)\;h_{j}=y_{2}-y_{1}}$

${\displaystyle (2)\;y_{2}={\frac {y_{1}}{2}}\left({\sqrt {1+8Fr_{1}^{2}}}-1\right)}$

Substitute y₂ equation into jump height equation:

${\displaystyle (3)\;h_{j}={\frac {y_{1}}{2}}\left({\sqrt {1+8Fr_{1}^{2}}}-1\right)-y_{1}}$

${\displaystyle (4)\;h_{j}={\frac {y_{1}{\sqrt {1+8Fr_{1}^{2}}}-3y_{1}}{2}}}$

Example 4: Height calculation

Given:

Use data from Example 2

Find:

Height of jump

Solution:

${\displaystyle (5)\;h_{j}={\frac {y_{1}{\sqrt {1+8Fr_{1}^{2}}}-3y_{1}}{2}}}$

${\displaystyle (6)\;h_{j}={\frac {0.5{\sqrt {1+8(4.5)^{2}}}-(3*0.5)}{2}}}$

${\displaystyle (7)\;h_{j}=2.4\;m}$

Types of jumps

A hydraulic jump can assume several distinct forms depending on the approach Froude number, Fr₁. Each of these types has unique flow patterns and flow characteristics, such as the strength and formation of rollers and eddies, that help to determine the amount of energy dissipation that will occur in the jump. The following descriptions of jump types are based on specific ranges of Froude numbers, but these ranges are not precise and that overlap can occur near the endpoints.

Weak jump (1 < Fr₁ < 2.5)

For the case when 1 < Fr₁ < 1.7, y₁ and y₂ are approximately equal and only a very small jump occurs. In this range, the water surface shows slight undulations and because of this, jumps in this range are sometimes known as undular jumps. These surface riffles generally result in very little energy dissipation. As Fr₁ approaches 1.7, a number of small rollers begin to form at the water surface at the jump location, but in general, the downstream water surface remains relatively smooth. Between 1.7 < Fr₁ < 2.5, the velocity remains fairly uniform on either side of the jump and energy loss is low.

Oscillating jump (2.5 < Fr₁ < 4.5)

An oscillating jump can occur when 2.5 < Fr₁ < 4.5. During this jump, the jet of water at the entrance of the jump (supercritical) fluctuates from the bottom of the channel to the top of the channel at an irregular period. Turbulence created from this jet can be near the channel bottom at one instant and then suddenly transition to the water surface. This oscillation of the jet causes irregular waves to form, which can propagate for long distances downstream of the jump, potentially causing damage and degradation of the channel banks.

Steady Jump (4.5 < Fr₁ < 9)

When the Froude number falls into this range, the jump forms steadily and at the same location. In a steady jump, turbulence is confined within the jump and the location of the jump is the least susceptible to downstream flow conditions out of the four major types of jumps. Steady jumps are generally well-balanced and the energy dissipation is usually considerable (45-70%).

Strong jump (Fr₁ > 9)

There is a large difference in conjugate depths in a strong jump. Strong jumps are characterized by a jump action that is very rough resulting in a high energy dissipation rate. At irregular intervals, slugs of water can be seen rolling down the front of the jump face. These slugs enter the high-velocity, supercritical jet and cause the formation of additional waves in the jump. Energy dissipation in strong jumps can reach up to 85%.

Jump location

In general, a hydraulic jump is formed at a location where the upstream and downstream flow depths satisfy the conjugate depth equation. However, there can be conditions in a channel, such as downstream controls, that can alter where the conjugate depths form. Tailwater depth can play a very influential role on where the jump will occur in the channel, and changes in this depth can shift the jump either upstream or downstream. Figure 6 contains three scenarios of tailwater elevations (y_d): y_d is equal to the conjugate depth (y₂) of the upstream flow depth (y₁), y_d is less than the conjugate depth (y₂) of the upstream flow depth (y₁), and y_d is greater than the conjugate depth (y₂) of the upstream flow depth (y₁). The upstream depth (y₁) in all three cases is controlled by a sluice gate and remains constant. Its corresponding conjugate depth (y₂) is shown by the dashed line in each of the scenarios.

In the first situation (Scenario A), the jump is formed right at the apron, as it would if there was no downstream control. However, in the next scenario (Scenario B), the downstream tailwater depth has some control imposed on it such that it is less than the conjugate to y₁. In this case, the jump travels downstream and initiates at a point where the upstream flow depth (y₁’) has risen to the conjugate of the new downstream tailwater depth (y_d). This rise from y₁ to y₁’ is caused by frictional resistance in the channel; and velocity decrease, the depth increase. In this image, y₁’ and y₂’ represent the conjugate depths of the hydraulic jump where y₂’ assumes the depth of y_d. In contrast, in the third setup (Scenario C), there is a downstream control that forces the tailwater elevation to a depth above the original conjugate depth. Here, y_d is greater than the required depth so the jump is pushed upstream. In this scenario, the sluice gate inhibits the movement of the jump upstream so that the upstream conjugate cannot be attained. This leads to a situation known as a submerged or drowned hydraulic jump. These scenarios demonstrate how influential the role of tailwater is to jump formation and location.

Classifications of hydraulic jumps

Classification by Froude number

Table 1. Hydraulic Jump Classifications

Froude number vs y₂/y₁

To help visualize the relationship of the upstream Froude number and the flow depth downstream of the hydraulic jump, it is helpful to plot y₂/y₁ versus the upstream Froude Number, Fr₁. (Figure 8) The value of y₂/y₁ is a ratio of depths that represent a dimensionless jump height; for example, if y₂/y₁ = 2, then the jump doubles the depth of flow. As the upstream Froude Number increases (moves toward more supercritical flow), the ratio of the downstream depth to the upstream depth also increases, and the graph verifies the existence of a positive linear relationship between the dimensionless jump height and the upstream Froude Number. This implies that a more supercritical upstream flow, y₁, will produce a larger downstream depth, y₂, and thus a larger jump. The relationship given in Figure 8 below was developed for a horizontal, rectangular channel with q = 10 ft/s. This graph is limited by the following due to the nature of a hydraulic jump:

1. y₂/y₁ > 1: depth increases over the jump so that y₂ > y₁

2. Fr₂ < 1: downstream flow must be subcritical

3. Fr₁ > 1: upstream flow must be supercritical

Table 2 shows the calculated values used to develop Figure 8. The values associated with a y₁ = 1.5 ft are not valid for use since they violate the above limits. The cusp of the above limits is reached at the critical depth, y_c, where all of these values are equal to 1. There will not, however, be a hydraulic jump in the situation where y₁ is equal to y_c.

Table 2. Values for Depth and Froude Number over Hydraulic Jump

q = 10 ft, g = 32.2 ft/s, y_c = 1.46 ft, y values in ft

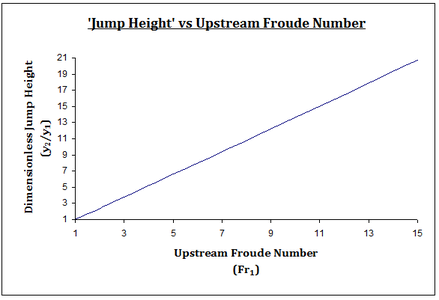
Figure 8. Dimensionless Jump Height vs. Upstream Froude Number (Please note that this diagram is not fully correct. Other factors taken into account are width and water velocity

This topic contribution was made in partial fulfillment of the requirements for Virginia Tech, Department of Civil and Environmental Engineering course: CEE 5984 – Open Channel Flow during the Fall 2010 semester.

References

1. Chanson, Hubert (2009). "Current knowledge in hydraulic jumps and related phenomena. A survey of experimental results" (PDF). European Journal of Mechanics B. 28 (2): 191–210. Bibcode:2009EuJMB..28..191C. doi:10.1016/j.euromechflu.2008.06.004.
2. Open-Channel Flow
3. Chanson, Hubert (2012). "Momentum Considerations in Hydraulic Jumps and Bores" (PDF). Journal of Irrigation and Drainage Engineering. 138 (4): 382–385. doi:10.1061/(ASCE)IR.1943-4774.0000409.
4. "Chapter 6 – HEC 14 – Hydraulics – Engineering – FHWA". Fhwa.dot.gov. 2006-10-16. Retrieved 2010-11-10.
5. "Surface Tension and the Hydraulic Jump".
6. "Surface Tension and the Hydraulic Jump". Math.mit.edu. Retrieved 2010-11-10.
8. "Archived copy" (PDF). Archived from the original (PDF) on 2011-10-05. Retrieved 2010-11-11.{{cite web}}: CS1 maint: archived copy as title (link)
9. Chaudhry, M. Hanif (2007-12-04). Open-Channel Flow. Springer. ISBN 978-0-387-30174-7.
10. Hager, W.H. 1992. Energy Dissipators and Hydraulic Jump. Kluwer Academic, Dordrecht, The Netherlands. ISBN 0-7923-1508-1
11. ^ Chow, V. T. (1959). Open-Channel Hydraulics, McGraw-Hill, New York, NY.
12. ^ Chaudhry, M. H. (2008). Open-Channel Flow, Springer Science+Business Media, LLC, New York, NY.
13. ^ Akan, A. O. (2006). Open Channel Hydraulics, Elsevier Ltd., Burlington, MA.

• Fluid mechanics
• Hydraulics
• Wave mechanics