This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|

Correlated color temperature (CCT, Tcp) refers to the temperature of a Planckian radiator whose perceived color most closely resembles that of a given stimulus at the same brightness and under specified viewing conditions."
Motivation
Black-body radiators are the reference by which the whiteness of light sources is judged. A black body is characterized by its temperature and emits light of a specific hue, which is referred to as color temperature. In practice, light sources that approximate Planckian radiators, such as certain fluorescent or high-intensity discharge lamps, are assessed based on their CCT, which is the temperature of a Planckian radiator whose color most closely resembles that of the light source. For light sources that do not follow the Planckian distribution, aligning them with a black body is not straightforward; thus, the concept of CCT is extended to represent these sources as accurately as possible on a one-dimensional color temperature scale, where "as accurately as possible" is determined within the framework of an objective color space.
Background
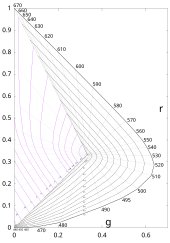



The notion of using Planckian radiators as a yardstick against which to judge other light sources is not new. In 1923, writing about "grading of illuminants with reference to quality of color ... the temperature of the source as an index of the quality of color", Priest essentially described CCT as we understand it today, going so far as to use the term "apparent color temperature", and astutely recognized three cases:
- "Those for which the spectral distribution of energy is identical with that given by the Planckian formula."
- "Those for which the spectral distribution of energy is not identical with that given by the Planckian formula, but still is of such a form that the quality of the color evoked is the same as would be evoked by the energy from a Planckian radiator at the given color temperature."
- "Those for which the spectral distribution of energy is such that the color can be matched only approximately by a stimulus of the Planckian form of spectral distribution."
Several important developments occurred in 1931. In chronological order:
- Raymond Davis published a paper on "correlated color temperature" (his term). Referring to the Planckian locus on the r-g diagram, he defined the CCT as the average of the "primary component temperatures" (RGB CCTs), using trilinear coordinates.
- The CIE announced the XYZ color space.
- Deane B. Judd published a paper on the nature of "least perceptible differences" with respect to chromatic stimuli. By empirical means he determined that the difference in sensation, which he termed ΔE for a "discriminatory step between colors ... Empfindung" (German for sensation) was proportional to the distance of the colors on the chromaticity diagram. Referring to the (r,g) chromaticity diagram depicted aside, he hypothesized that
- K ΔE = |c1 − c2| = max(|r1 − r2|, |g1 − g2|).
These developments paved the way for the development of new chromaticity spaces that are more suited to estimating correlated color temperatures and chromaticity differences. Bridging the concepts of color difference and color temperature, Priest made the observation that the eye is sensitive to constant differences in "reciprocal" temperature:
A difference of one micro-reciprocal-degree (μrd) is fairly representative of the doubtfully perceptible difference under the most favorable conditions of observation.
Priest proposed to use "the scale of temperature as a scale for arranging the chromaticities of the several illuminants in a serial order". Over the next few years, Judd published three more significant papers:
The first verified the findings of Priest, Davis, and Judd, with a paper on sensitivity to change in color temperature.
The second proposed a new chromaticity space, guided by a principle that has become the holy grail of color spaces: perceptual uniformity (chromaticity distance should be commensurate with perceptual difference). By means of a projective transformation, Judd found a more "uniform chromaticity space" (UCS) in which to find the CCT. Judd determined the "nearest color temperature" by simply finding the point on the Planckian locus nearest to the chromaticity of the stimulus on Maxwell's color triangle, depicted aside. The transformation matrix he used to convert X,Y,Z tristimulus values to R,G,B coordinates was:
From this, one can find these chromaticities:
The third depicted the locus of the isothermal chromaticities on the CIE 1931 x,y chromaticity diagram. Since the isothermal points formed normals on his UCS diagram, transformation back into the xy plane revealed them still to be lines, but no longer perpendicular to the locus.
Calculation

Judd's idea of determining the nearest point to the Planckian locus on a uniform chromaticity space is current. In 1937, MacAdam suggested a "modified uniform chromaticity scale diagram", based on certain simplifying geometrical considerations:
This (u,v) chromaticity space became the CIE 1960 color space, which is still used to calculate the CCT (even though MacAdam did not devise it with this purpose in mind). Using other chromaticity spaces, such as u'v', leads to non-standard results that may nevertheless be perceptually meaningful.

The distance from the locus (i.e., degree of departure from a black body) is traditionally indicated in units of Δuv; positive for points above the locus. This concept of distance has evolved to become CIELAB ΔE*, which continues to be used today.
Robertson's method
Before the advent of powerful personal computers, it was common to estimate the correlated color temperature by way of interpolation from look-up tables and charts. The most famous such method is Robertson's, who took advantage of the relatively even spacing of the mired scale (see above) to calculate the CCT Tc using linear interpolation of the isotherm's mired values:
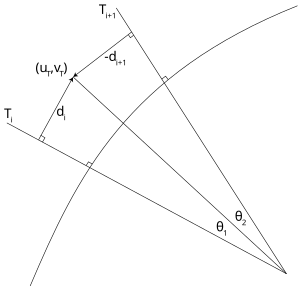
where and are the color temperatures of the look-up isotherms and i is chosen such that . (Furthermore, the test chromaticity lies between the only two adjacent lines for which .)
If the isotherms are tight enough, one can assume , leading to
The distance of the test point to the i-th isotherm is given by
where is the chromaticity coordinate of the i-th isotherm on the Planckian locus and mi is the isotherm's slope. Since it is perpendicular to the locus, it follows that where li is the slope of the locus at .
Precautions
Although the CCT can be calculated for any chromaticity coordinate, the result is meaningful only if the light source somewhat approximates a Planckian radiator. The CIE recommends that "The concept of correlated color temperature should not be used if the chromaticity of the test source differs more than Δuv = 5×10 from the Planckian radiator." Beyond a certain value of Δuv, a chromaticity co-ordinate may be equidistant to two points on the locus, causing ambiguity in the CCT.
Approximation
If a narrow range of color temperatures is considered—those encapsulating daylight being the most practical case—one can approximate the Planckian locus in order to calculate the CCT in terms of chromaticity coordinates. Following Kelly's observation that the isotherms intersect in the purple region near (x = 0.325, y = 0.154), McCamy proposed this cubic approximation:
where n = (x − xe)/(y - ye) is the inverse slope line, and (xe = 0.3320, ye = 0.1858) is the "epicenter"; quite close to the intersection point mentioned by Kelly. The maximum absolute error for color temperatures ranging from 2856 K (illuminant A) to 6504 K (D65) is under 2 K.
Hernández-André's 1999 proposal, using exponential terms, considerably extends the applicable range by adding a second epicenter for high color temperatures:
where n is as before and the other constants are defined below:
| 3–50 kK | 50–800 kK | |
|---|---|---|
| xe | 0.3366 | 0.3356 |
| ye | 0.1735 | 0.1691 |
| A0 | −949.86315 | 36284.48953 |
| A1 | 6253.80338 | 0.00228 |
| t1 | 0.92159 | 0.07861 |
| A2 | 28.70599 | 5.4535×10 |
| t2 | 0.20039 | 0.01543 |
| A3 | 0.00004 | |
| t3 | 0.07125 |
The author suggests that one use the low-temperature equation to determine whether the higher-temperature parameters are needed.
Ohno (2013) proposes an accurate combined method based on a lookup table, a "parabolic" search, and a "triangular" search. The paper stresses the importance of also returning the Δuv value for evalulation of light sources. As it does not use one fixed table, it can be applied to any observer color matching function.
The inverse calculation, from color temperature to corresponding chromaticity coordinates, is discussed in Planckian locus § Approximation.
References
- CIE/IEC 17.4:1987 International Lighting Vocabulary Archived 2010-02-27 at the Wayback Machine (ISBN 3900734070)
- Borbély, Ákos; Sámson, Árpád; Schanda, János (December 2001). "The concept of correlated colour temperature revisited". Color Research & Application. 26 (6): 450–457. doi:10.1002/col.1065. Archived from the original on 2009-02-05.
- "The Color White". Architect Magazine. 19 March 2007. Retrieved 16 July 2024.
- "What is CCT?". Anova Lighting. 30 May 2024. Retrieved 16 July 2024.
- "Effects of illuminance and correlated color temperature of indoor light on emotion perception". Nature. 12 July 2021. Retrieved 16 July 2024.
- Hyde, Edward P. (June 1911). "A New Determination of the Selective Radiation from Tantalum (abstract)". Physical Review. Series I. 32 (6). The American Physical Society: 632–633. doi:10.1103/PhysRevSeriesI.32.632.
This existence of a color match is a consequence of there being approximately the same energy distribution in the visible spectra.
- ^ Priest, Irwin G. (1923). "The colorimetry and photometry of daylight ·and incandescent illuminants by the method of rotatory dispersion". JOSA. 7 (12): 1175–1209. Bibcode:1923JOSA....7.1175P. doi:10.1364/JOSA.7.001175.
The color temperature of a source is the temperature at which a Planckian radiator would emit radiant energy competent to evoke a color of the same quality as that evoked by the radiant energy from the source in question. The color temperature is not necessarily the same as the 'true temperature' of the source; but this circumstance has no significance whatever in the use of the color temperature as a means to the end of establishing a scale for the quality of the color of illuminants. For this purpose no knowledge of the temperature of the source nor indeed of its emissive properties is required. All that is involved in giving the color temperature of any illuminant is the affirmation that the color of the luminant is of the same quality as the color of a Planckian radiator at the given temperature.
- ^ Davis, Raymond (1931). "A Correlated Color Temperature for Illuminants". Bureau of Standards Journal of Research. 7 (4): 659–681. doi:10.6028/jres.007.039.
The ideal correlated colour temperature of a light source is the absolute temperature at which the Planckian radiator emits radiant energy component to evoke a colour which, of all Planckian colours, most closely approximates the colour evoked by the source in question.
from Research Paper 365 - ^ Judd, Deane B. (1931). "Chromaticity sensibility to stimulus differences". JOSA. 22 (2): 72–108. doi:10.1364/JOSA.22.000072.
- Priest, Irwin G. (February 1933). "A proposed scale for use in specifying the chromaticity of incandescent illuminants and various phases of daylight". JOSA. 23 (2): 42. Bibcode:1933JOSA...23...41P. doi:10.1364/JOSA.23.000041.
- Judd, Deane B. (January 1933). "Sensibility to Color-Temperature Change as a Function of Temperature". JOSA. 23 (1): 7. Bibcode:1933JOSA...23....7J. doi:10.1364/JOSA.23.000007.
Regarding (Davis, 1931): This simpler statement of the spectral-centroid relation might have been deduced by combining two previous findings, one by Gibson (see footnote 10, p. 12) concerning a spectral-centroid relation between incident and transmitted light for daylight filters, the other by Langmuir and Orange (Trans. A.I.E.E., 32, 1944–1946 (1913)) concerning a similar relation involving reciprocal temperature. The mathematical analysis on which this latter finding is based was given later by Foote, Mohler and Fairchild, J. Wash. Acad. Sci. 7, 545–549 (1917), and Gage, Trans. I.E.S. 16, 428–429 (1921) also called attention to this relation.
- Judd, Deane B. (January 1935). "A Maxwell Triangle Yielding Uniform Chromaticity Scales" (PDF). JOSA. 25 (1): 24–35. Bibcode:1935JOSA...25...24J. doi:10.1364/JOSA.25.000024. Archived (PDF) from the original on 2017-01-30.
An important application of this coordinate system is its use in finding from any series of colors the one most resembling a neighboring color of the same brilliance, for example, the finding of the nearest color temperature for a neighboring non-Planckian stimulus. The method is to draw the shortest line from the point representing the non-Planckian stimulus to the Planckian locus.
- OSA Committee on Colorimetry (November 1944). "Quantitative data and methods for colorimetry". JOSA. 34 (11): 633–688. Bibcode:1944JOSA...34..633C. doi:10.1364/JOSA.34.000633. (recommended reading)
- Judd, Deane B. (November 1936). "Estimation of Chromaticity Differences and Nearest Color Temperatures on the Standard 1931 I.C.I. Colorimetric Coordinate System" (PDF). JOSA. 26 (11): 421–426. Bibcode:1936JOSA...26..421J. doi:10.1364/JOSA.26.000421. Archived (PDF) from the original on 2017-02-11.
- MacAdam, David L. (August 1937). "Projective transformations of I.C.I. color specifications". JOSA. 27 (8): 294–299. Bibcode:1937JOSA...27..294M. doi:10.1364/JOSA.27.000294.
- The CIE definition of correlated color temperature (removed) Archived 2009-02-05 at the Wayback Machine
- Schanda, János; Danyi, M. (1977). "Correlated Color-Temperature Calculations in the CIE 1976 Chromaticity Diagram". Color Research & Application. 2 (4). Wiley Interscience: 161–163. doi:10.1002/col.5080020403.
Correlated color temperature can be calculated using the new diagram, leading to somewhat different results than those calculated according to the CIE 1960 uv diagram.
- ^ Kelly, Kenneth L. (August 1963). "Lines of Constant Correlated Color Temperature Based on MacAdam's (u,v) Uniform Chromaticity Transformation of the CIE Diagram". JOSA. 53 (8): 999–1002. Bibcode:1963JOSA...53..999K. doi:10.1364/JOSA.53.000999.
- Robertson, Alan R. (November 1968). "Computation of Correlated Color Temperature and Distribution Temperature". JOSA. 58 (11): 1528–1535. Bibcode:1968JOSA...58.1528R. doi:10.1364/JOSA.58.001528.
- ANSI C implementation Archived 2008-04-22 at the Wayback Machine, Bruce Lindbloom
- Walter, Wolfgang (February 1992). "Determination of correlated color temperature based on a color-appearance model". Color Research & Application. 17 (1): 24–30. doi:10.1002/col.5080170107.
The concept of correlated color temperature is only useful for lamps with chromaticity points close to the black body...
- Schanda, János (2007). "3: CIE Colorimetry". Colorimetry: Understanding the CIE System. Wiley Interscience. pp. 37–46. doi:10.1002/9780470175637.ch3. ISBN 978-0-470-04904-4.
- McCamy, Calvin S. (April 1992). "Correlated color temperature as an explicit function of chromaticity coordinates". Color Research & Application. 17 (2): 142–144. doi:10.1002/col.5080170211. plus erratum doi:10.1002/col.5080180222
- Hernández-Andrés, Javier; Lee, RL; Romero, J (September 20, 1999). "Calculating Correlated Color Temperatures Across the Entire Gamut of Daylight and Skylight Chromaticities" (PDF). Applied Optics. 38 (27): 5703–5709. Bibcode:1999ApOpt..38.5703H. doi:10.1364/AO.38.005703. PMID 18324081. Archived (PDF) from the original on April 1, 2016.
- Ohno, Yoshi (2 January 2014). "Practical Use and Calculation of CCT and Duv". LEUKOS. 10 (1): 47–55. doi:10.1080/15502724.2014.839020. S2CID 122251872.
- "colour.temperature.uv_to_CCT_Ohno2013 — Colour 0.4.4 documentation". colour.readthedocs.io.



 in the CIE 1960 UCS.
in the CIE 1960 UCS.
 and
and  are the color temperatures of the look-up isotherms and i is chosen such that
are the color temperatures of the look-up isotherms and i is chosen such that  . (Furthermore, the test chromaticity lies between the only two adjacent lines for which
. (Furthermore, the test chromaticity lies between the only two adjacent lines for which  .)
.)
 , leading to
, leading to


 is the chromaticity coordinate of the i-th isotherm on the Planckian locus and mi is the isotherm's
is the chromaticity coordinate of the i-th isotherm on the Planckian locus and mi is the isotherm's  where li is the slope of the locus at
where li is the slope of the locus at 
