The Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes and plasmas. It is a linearized Poisson–Boltzmann model, which assumes an extremely simplified model of electrolyte solution but nevertheless gave accurate predictions of mean activity coefficients for ions in dilute solution. The Debye–Hückel equation provides a starting point for modern treatments of non-ideality of electrolyte solutions.
Overview
In the chemistry of electrolyte solutions, an ideal solution is a solution whose colligative properties are proportional to the concentration of the solute. Real solutions may show departures from this kind of ideality. In order to accommodate these effects in the thermodynamics of solutions, the concept of activity was introduced: the properties are then proportional to the activities of the ions. Activity, a, is proportional to concentration, c. The proportionality constant is known as an activity coefficient, .
In an ideal electrolyte solution the activity coefficients for all the ions are equal to one. Ideality of an electrolyte solution can be achieved only in very dilute solutions. Non-ideality of more concentrated solutions arises principally (but not exclusively) because ions of opposite charge attract each other due to electrostatic forces, while ions of the same charge repel each other. In consequence ions are not randomly distributed throughout the solution, as they would be in an ideal solution.
Activity coefficients of single ions cannot be measured experimentally because an electrolyte solution must contain both positively charged ions and negatively charged ions. Instead, a mean activity coefficient, is defined. For example, with the electrolyte NaCl
In general, the mean activity coefficient of a fully dissociated electrolyte of formula AnBm is given by
Activity coefficients are themselves functions of concentration as the amount of inter-ionic interaction increases as the concentration of the electrolyte increases. Debye and Hückel developed a theory with which single ion activity coefficients could be calculated. By calculating the mean activity coefficients from them the theory could be tested against experimental data. It was found to give excellent agreement for "dilute" solutions.
Further information: Bates–Guggenheim ConventionThe model
A description of Debye–Hückel theory includes a very detailed discussion of the assumptions and their limitations as well as the mathematical development and applications.
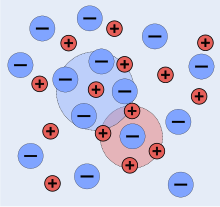
A snapshot of a 2-dimensional section of an idealized electrolyte solution is shown in the picture. The ions are shown as spheres with unit electrical charge. The solvent (pale blue) is shown as a uniform medium, without structure. On average, each ion is surrounded more closely by ions of opposite charge than by ions of like charge. These concepts were developed into a quantitative theory involving ions of charge z1e and z2e, where z can be any integer. The principal assumption is that departure from ideality is due to electrostatic interactions between ions, mediated by Coulomb's law: the force of interaction between two electric charges, separated by a distance, r in a medium of relative permittivity εr is given by
It is also assumed that
- The solute is completely dissociated; it is a strong electrolyte.
- Ions are spherical and are not polarized by the surrounding electric field. Solvation of ions is ignored except insofar as it determines the effective sizes of the ions.
- The solvent plays no role other than providing a medium of constant relative permittivity (dielectric constant).
- There is no electrostriction.
- Individual ions surrounding a "central" ion can be represented by a statistically averaged cloud of continuous charge density, with a minimum distance of closest approach.
The last assumption means that each cation is surrounded by a spherically symmetric cloud of other ions. The cloud has a net negative charge. Similarly each anion is surrounded by a cloud with net positive charge.
Mathematical development
The deviation from ideality is taken to be a function of the potential energy resulting from the electrostatic interactions between ions and their surrounding clouds. To calculate this energy two steps are needed.
The first step is to specify the electrostatic potential for ion j by means of Poisson's equation
ψ(r) is the total potential at a distance, r, from the central ion and ρ(r) is the averaged charge density of the surrounding cloud at that distance. To apply this formula it is essential that the cloud has spherical symmetry, that is, the charge density is a function only of distance from the central ion as this allows the Poisson equation to be cast in terms of spherical coordinates with no angular dependence.
The second step is to calculate the charge density by means of a Boltzmann distribution.
where kB is Boltzmann constant and T is the temperature. This distribution also depends on the potential ψ(r) and this introduces a serious difficulty in terms of the superposition principle. Nevertheless, the two equations can be combined to produce the Poisson–Boltzmann equation.
Solution of this equation is far from straightforward. Debye and Hückel expanded the exponential as a truncated Taylor series to first order. The zeroth order term vanishes because the solution is on average electrically neutral (so that Σ ni zi = 0), which leaves us with only the first order term. The result has the form of the Helmholtz equation
- ,
which has an analytical solution. This equation applies to electrolytes with equal numbers of ions of each charge. Nonsymmetrical electrolytes require another term with ψ. For symmetrical electrolytes, this reduces to the modified spherical Bessel equation
The coefficients and are fixed by the boundary conditions. As , must not diverge, so . At , which is the distance of the closest approach of ions, the force exerted by the charge should be balanced by the force of other ions, imposing , from which is found, yielding
The electrostatic potential energy, , of the ion at is
This is the potential energy of a single ion in a solution. The multiple-charge generalization from electrostatics gives an expression for the potential energy of the entire solution. The mean activity coefficient is given by the logarithm of this quantity as follows

where I is the ionic strength and a0 is a parameter that represents the distance of closest approach of ions. For aqueous solutions at 25 °C A = 0.51 moldm and B = 3.29 nmmoldm
is a constant that depends on temperature. If is expressed in terms of molality, instead of molarity (as in the equation above and in the rest of this article), then an experimental value for of water is at 25 °C. It is common to use a base-10 logarithm, in which case we factor , so A is . The multiplier before in the equation is for the case when the dimensions of are . When the dimensions of are , the multiplier must be dropped from the equation
The most significant aspect of this result is the prediction that the mean activity coefficient is a function of ionic strength rather than the electrolyte concentration. For very low values of the ionic strength the value of the denominator in the expression above becomes nearly equal to one. In this situation the mean activity coefficient is proportional to the square root of the ionic strength. This is known as the Debye–Hückel limiting law. In this limit the equation is given as follows
The excess osmotic pressure obtained from Debye–Hückel theory is in cgs units: Therefore, the total pressure is the sum of the excess osmotic pressure and the ideal pressure . The osmotic coefficient is then given by
Nondimensionalization
Taking the differential equation from earlier (as stated above, the equation only holds for low concentrations):
Using the Buckingham π theorem on this problem results in the following dimensionless groups: is called the reduced scalar electric potential field. is called the reduced radius. The existing groups may be recombined to form two other dimensionless groups for substitution into the differential equation. The first is what could be called the square of the reduced inverse screening length, . The second could be called the reduced central ion charge, (with a capital Z). Note that, though is already dimensionless, without the substitution given below, the differential equation would still be dimensional.
To obtain the nondimensionalized differential equation and initial conditions, use the groups to eliminate in favor of , then eliminate in favor of while carrying out the chain rule and substituting , then eliminate in favor of (no chain rule needed), then eliminate in favor of , then eliminate in favor of . The resulting equations are as follows:
For table salt in 0.01 M solution at 25 °C, a typical value of is 0.0005636, while a typical value of is 7.017, highlighting the fact that, in low concentrations, is a target for a zero order of magnitude approximation such as perturbation analysis. Unfortunately, because of the boundary condition at infinity, regular perturbation does not work. The same boundary condition prevents us from finding the exact solution to the equations. Singular perturbation may work, however.
Limitations and extensions
This equation for gives satisfactory agreement with experimental measurements for low electrolyte concentrations, typically less than 10 mol/L. Deviations from the theory occur at higher concentrations and with electrolytes that produce ions of higher charges, particularly unsymmetrical electrolytes. Essentially these deviations occur because the model is oversimplified, so there is little to be gained making small adjustments to the model. The individual assumptions can be challenged in turn.
- Complete dissociation. Ion association may take place, particularly with ions of higher charge. This was followed up in detail by Niels Bjerrum. The Bjerrum length is the separation at which the electrostatic interaction between two ions is comparable in magnitude to kT.
- Weak electrolytes. A weak electrolyte is one that is not fully dissociated. As such it has a dissociation constant. The dissociation constant can be used to calculate the extent of dissociation and hence, make the necessary correction needed to calculate activity coefficients.
- Ions are spherical, not point charges and are not polarized. Many ions such as the nitrate ion, NO3, are not spherical. Polyatomic ions are also polarizable.
- Role of the solvent. The solvent is not a structureless medium but is made up of molecules. The water molecules in aqueous solution are both dipolar and polarizable. Both cations and anions have a strong primary solvation shell and a weaker secondary solvation shell. Ion–solvent interactions are ignored in Debye–Hückel theory.
Moreover, ionic radius is assumed to be negligible, but at higher concentrations, the ionic radius becomes comparable to the radius of the ionic atmosphere. Most extensions to Debye–Hückel theory are empirical in nature. They usually allow the Debye–Hückel equation to be followed at low concentration and add further terms in some power of the ionic strength to fit experimental observations. The main extensions are the Davies equation, Pitzer equations and specific ion interaction theory.
One such extended Debye–Hückel equation is given by: where as its common logarithm is the activity coefficient, is the integer charge of the ion (1 for H, 2 for Mg etc.), is the ionic strength of the aqueous solution, and is the size or effective diameter of the ion in angstrom. The effective hydrated radius of the ion, a is the radius of the ion and its closely bound water molecules. Large ions and less highly charged ions bind water less tightly and have smaller hydrated radii than smaller, more highly charged ions. Typical values are 3Å for ions such as H, Cl, CN, and HCOO. The effective diameter for the hydronium ion is 9Å. and are constants with values of respectively 0.5085 and 0.3281 at 25 °C in water .
The extended Debye–Hückel equation provides accurate results for μ ≤ 0.1. For solutions of greater ionic strengths, the Pitzer equations should be used. In these solutions the activity coefficient may actually increase with ionic strength.

The Debye–Hückel equation cannot be used in the solutions of surfactants where the presence of micelles influences on the electrochemical properties of the system (even rough judgement overestimates γ for ~50%).
Electrolytes mixtures
The theory can be applied also to dilute solutions of mixed electrolytes. Freezing point depression measurements has been used to this purpose.
Conductivity

The treatment given so far is for a system not subject to an external electric field. When conductivity is measured the system is subject to an oscillating external field due to the application of an AC voltage to electrodes immersed in the solution. Debye and Hückel modified their theory in 1926 and their theory was further modified by Lars Onsager in 1927. All the postulates of the original theory were retained. In addition it was assumed that the electric field causes the charge cloud to be distorted away from spherical symmetry. After taking this into account, together with the specific requirements of moving ions, such as viscosity and electrophoretic effects, Onsager was able to derive a theoretical expression to account for the empirical relation known as Kohlrausch's Law, for the molar conductivity, Λm.
is known as the limiting molar conductivity, K is an empirical constant and c is the electrolyte concentration. Limiting here means "at the limit of the infinite dilution"). Onsager's expression is
where A and B are constants that depend only on known quantities such as temperature, the charges on the ions and the dielectric constant and viscosity of the solvent. This is known as the Debye–Hückel–Onsager equation. However, this equation only applies to very dilute solutions and has been largely superseded by other equations due to Fuoss and Onsager, 1932 and 1957 and later.
Summary of Debye and Hückel's first article on the theory of dilute electrolytes
The English title of the article is "On the Theory of Electrolytes. I. Freezing Point Depression and Related Phenomena". It was originally published in 1923 in volume 24 of a German-language journal Physikalische Zeitschrift. An English translation of the article is included in a book of collected papers presented to Debye by "his pupils, friends, and the publishers on the occasion of his seventieth birthday on March 24, 1954". Another English translation was completed in 2019. The article deals with the calculation of properties of electrolyte solutions that are under the influence of ion-induced electric fields, thus it deals with electrostatics.
In the same year they first published this article, Debye and Hückel, hereinafter D&H, also released an article that covered their initial characterization of solutions under the influence of electric fields called "On the Theory of Electrolytes. II. Limiting Law for Electric Conductivity", but that subsequent article is not (yet) covered here.
In the following summary (as yet incomplete and unchecked), modern notation and terminology are used, from both chemistry and mathematics, in order to prevent confusion. Also, with a few exceptions to improve clarity, the subsections in this summary are (very) condensed versions of the same subsections of the original article.
Introduction
D&H note that the Guldberg–Waage formula for electrolyte species in chemical reaction equilibrium in classical form is where
- is a notation for multiplication,
- is a dummy variable indicating the species,
- is the number of species participating in the reaction,
- is the mole fraction of species ,
- is the stoichiometric coefficient of species ,
- K is the equilibrium constant.
D&H say that, due to the "mutual electrostatic forces between the ions", it is necessary to modify the Guldberg–Waage equation by replacing with , where is an overall activity coefficient, not a "special" activity coefficient (a separate activity coefficient associated with each species)—which is what is used in modern chemistry as of 2007.
The relationship between and the special activity coefficients is
Fundamentals
D&H use the Helmholtz and Gibbs free entropies and to express the effect of electrostatic forces in an electrolyte on its thermodynamic state. Specifically, they split most of the thermodynamic potentials into classical and electrostatic terms: where
- is Helmholtz free entropy,
- is entropy,
- is internal energy,
- is temperature,
- is Helmholtz free energy.
D&H give the total differential of as where
By the definition of the total differential, this means that which are useful further on.
As stated previously, the internal energy is divided into two parts: where
- indicates the classical part,
- indicates the electric part.
Similarly, the Helmholtz free entropy is also divided into two parts:
D&H state, without giving the logic, that
It would seem that, without some justification,
Without mentioning it specifically, D&H later give what might be the required (above) justification while arguing that , an assumption that the solvent is incompressible.
The definition of the Gibbs free entropy is where is Gibbs free energy.
D&H give the total differential of as
At this point D&H note that, for water containing 1 mole per liter of potassium chloride (nominal pressure and temperature aren't given), the electric pressure amounts to 20 atmospheres. Furthermore, they note that this level of pressure gives a relative volume change of 0.001. Therefore, they neglect change in volume of water due to electric pressure, writing and put
D&H say that, according to Planck, the classical part of the Gibbs free entropy is where
- is a species,
- is the number of different particle types in solution,
- is the number of particles of species i,
- is the particle specific Gibbs free entropy of species i,
- is the Boltzmann constant,
- is the mole fraction of species i.
Species zero is the solvent. The definition of is as follows, where lower-case letters indicate the particle specific versions of the corresponding extensive properties:
D&H don't say so, but the functional form for may be derived from the functional dependence of the chemical potential of a component of an ideal mixture upon its mole fraction.
D&H note that the internal energy of a solution is lowered by the electrical interaction of its ions, but that this effect can't be determined by using the crystallographic approximation for distances between dissimilar atoms (the cube root of the ratio of total volume to the number of particles in the volume). This is because there is more thermal motion in a liquid solution than in a crystal. The thermal motion tends to smear out the natural lattice that would otherwise be constructed by the ions. Instead, D&H introduce the concept of an ionic atmosphere or cloud. Like the crystal lattice, each ion still attempts to surround itself with oppositely charged ions, but in a more free-form manner; at small distances away from positive ions, one is more likely to find negative ions and vice versa.
The potential energy of an arbitrary ion solution
Electroneutrality of a solution requires that where
- is the total number of ions of species i in the solution,
- is the charge number of species i.
To bring an ion of species i, initially far away, to a point within the ion cloud requires interaction energy in the amount of , where is the elementary charge, and is the value of the scalar electric potential field at . If electric forces were the only factor in play, the minimal-energy configuration of all the ions would be achieved in a close-packed lattice configuration. However, the ions are in thermal equilibrium with each other and are relatively free to move. Thus they obey Boltzmann statistics and form a Boltzmann distribution. All species' number densities are altered from their bulk (overall average) values by the corresponding Boltzmann factor , where is the Boltzmann constant, and is the temperature. Thus at every point in the cloud
Note that in the infinite temperature limit, all ions are distributed uniformly, with no regard for their electrostatic interactions.
The charge density is related to the number density:
When combining this result for the charge density with the Poisson equation from electrostatics, a form of the Poisson–Boltzmann equation results:
This equation is difficult to solve and does not follow the principle of linear superposition for the relationship between the number of charges and the strength of the potential field. It has been solved analyticallt by the Swedish mathematician Thomas Hakon Gronwall and his collaborators physical chemists V. K. La Mer and Karl Sandved in a 1928 article from Physikalische Zeitschrift dealing with extensions to Debye–Huckel theory.
However, for sufficiently low concentrations of ions, a first-order Taylor series expansion approximation for the exponential function may be used ( for ) to create a linear differential equation. D&H say that this approximation holds at large distances between ions, which is the same as saying that the concentration is low. Lastly, they claim without proof that the addition of more terms in the expansion has little effect on the final solution. Thus
The Poisson–Boltzmann equation is transformed to because the first summation is zero due to electroneutrality.
Factor out the scalar potential and assign the leftovers, which are constant, to . Also, let be the ionic strength of the solution:
So, the fundamental equation is reduced to a form of the Helmholtz equation:
Today, is called the Debye screening length. D&H recognize the importance of the parameter in their article and characterize it as a measure of the thickness of the ion atmosphere, which is an electrical double layer of the Gouy–Chapman type.
The equation may be expressed in spherical coordinates by taking at some arbitrary ion:
The equation has the following general solution (keep in mind that is a positive constant): where , , and are undetermined constants
The electric potential is zero at infinity by definition, so must be zero.
In the next step, D&H assume that there is a certain radius , beyond which no ions in the atmosphere may approach the (charge) center of the singled out ion. This radius may be due to the physical size of the ion itself, the sizes of the ions in the cloud, and any water molecules that surround the ions. Mathematically, they treat the singled out ion as a point charge to which one may not approach within the radius .
The potential of a point charge by itself is
D&H say that the total potential inside the sphere is where is a constant that represents the potential added by the ionic atmosphere. No justification for being a constant is given. However, one can see that this is the case by considering that any spherical static charge distribution is subject to the mathematics of the shell theorem. The shell theorem says that no force is exerted on charged particles inside a sphere (of arbitrary charge). Since the ion atmosphere is assumed to be (time-averaged) spherically symmetric, with charge varying as a function of radius , it may be represented as an infinite series of concentric charge shells. Therefore, inside the radius , the ion atmosphere exerts no force. If the force is zero, then the potential is a constant (by definition).
In a combination of the continuously distributed model which gave the Poisson–Boltzmann equation and the model of the point charge, it is assumed that at the radius , there is a continuity of and its first derivative. Thus
By the definition of electric potential energy, the potential energy associated with the singled out ion in the ion atmosphere is
Notice that this only requires knowledge of the charge of the singled out ion and the potential of all the other ions.
To calculate the potential energy of the entire electrolyte solution, one must use the multiple-charge generalization for electric potential energy:
The additional electric term to the thermodynamic potential
| This article is missing information about not yet added. Please expand the article to include this information. Further details may exist on the talk page. (May 2018) |
Experimental verification of the theory
To verify the validity of the Debye–Hückel theory, many experimental ways have been tried, measuring the activity coefficients: the problem is that we need to go towards very high dilutions. Typical examples are: measurements of vapour pressure, freezing point, osmotic pressure (indirect methods) and measurement of electric potential in cells (direct method). Going towards high dilutions good results have been found using liquid membrane cells, it has been possible to investigate aqueous media 10 M and it has been found that for 1:1 electrolytes (as NaCl or KCl) the Debye–Hückel equation is totally correct, but for 2:2 or 3:2 electrolytes it is possible to find negative deviation from the Debye–Hückel limit law: this strange behavior can be observed only in the very dilute area, and in more concentrate regions the deviation becomes positive. It is possible that Debye–Hückel equation is not able to foresee this behavior because of the linearization of the Poisson–Boltzmann equation, or maybe not: studies about this have been started only during the last years of the 20th century because before it wasn't possible to investigate the 10 M region, so it is possible that during the next years new theories will be born.
See also
- Electrolyte
- Chemical activity
- Ionic strength
- Poisson-Boltzmann equation
- Debye length
- Bjerrum length
- Bates-Guggenheim Convention
- Ionic atmosphere
- Electrical double layer
- Ion association
- Davies equation
- Pitzer equation
- Specific ion Interaction Theory
References
- P. Debye and E. Hückel (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen". Physikalische Zeitschrift. 24: 185–206.
- Wright, M.R. (2007). An Introduction to Aqueous Electrolyte Solutions. Wiley. ISBN 978-0-470-84293-5.
- Wright, section 1.10
- Wright, Section 8.23
- Wright, chapter 10.
- Wright, Section 10.3
- Wright, Section 10.3
- Wright, section 10.6.3
- Wright, section 10.6.8
- Wright, section 10.6.10
- Wright, section 10.6.15
- Data from Wright, Worked problem 8.17
- Wright, section 10.7
- ^ Hamann, Hamnett, and Vielstich (1998). Electrochemistry. Weinheim: Wiley-VCH Verlag GmbH. ISBN 3-527-29096-6.
{{cite book}}: CS1 maint: multiple names: authors list (link) - http://homepages.rpi.edu/~keblip/THERMO/chapters/Chapter33.pdf, page 9.
- Wright, section 10.9.
- Davies, C. W. (1962). Ion Association. London: Butterworths. pp. 37–53.
- R. Wasoe, Phys. Z., 30 (1929), 412
- Wright, section 12.3
- Wright, sections 12.10 to 12.17
- ^ The Collected Papers of Peter J. W. Debye. New York, New York: Interscience Publishers, Inc. 1954.
- P. Debye and E. Hückel (1923). "Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen". Physikalische Zeitschrift. 24: 185–206.
- Salzman, William R. (2001-08-21). "Mixtures; Partial Molar Quantities; Ideal Solutions". Chemical Thermodynamics. University of Arizona. Archived from the original on 2007-06-07. Retrieved 2007-10-23.
- http://www.pma.caltech.edu/Courses/ph136/yr2006/text.html Archived 2007-08-28 at the Wayback Machine, section 19.3
- Hille, Einar (1932). "Thomas Hakon Gronwall—In memoriam". Bull. Amer. Math. Soc. 38 (11): 775–786. doi:10.1090/s0002-9904-1932-05492-1. MR 1562506.
- http://guava.physics.uiuc.edu/~nigel/courses/569/Essays_2004/files/lu.pdf section 3.1)
- "LaPlace's and Poisson's Equations".
- "Electric potential of a charged sphere".
 .
.

 is defined. For example, with the electrolyte NaCl
is defined. For example, with the electrolyte NaCl






 ,
,
 and
and  are fixed by the boundary conditions. As
are fixed by the boundary conditions. As  ,
,  must not diverge, so
must not diverge, so  . At
. At  , which is the distance of the closest approach of ions, the force exerted by the charge should be balanced by the force of other ions, imposing
, which is the distance of the closest approach of ions, the force exerted by the charge should be balanced by the force of other ions, imposing  , from which
, from which 
 , of the ion at
, of the ion at  is
is

 values for KBr at 25°C (points) and Debye–Hückel limiting law (coloured line)
values for KBr at 25°C (points) and Debye–Hückel limiting law (coloured line)


 is a constant that depends on temperature. If
is a constant that depends on temperature. If  is expressed in terms of molality, instead of molarity (as in the equation above and in the rest of this article), then an experimental value for
is expressed in terms of molality, instead of molarity (as in the equation above and in the rest of this article), then an experimental value for  at 25 °C. It is common to use a base-10 logarithm, in which case we factor
at 25 °C. It is common to use a base-10 logarithm, in which case we factor  , so A is
, so A is  . The multiplier
. The multiplier  before
before  in the equation is for the case when the dimensions of
in the equation is for the case when the dimensions of  . When the dimensions of
. When the dimensions of  , the multiplier
, the multiplier 
 Therefore, the total pressure is the sum of the excess osmotic pressure and the ideal pressure
Therefore, the total pressure is the sum of the excess osmotic pressure and the ideal pressure  . The
. The 


 is called the reduced scalar electric potential field.
is called the reduced scalar electric potential field.  is called the reduced radius. The existing groups may be recombined to form two other dimensionless groups for substitution into the differential equation. The first is what could be called the square of the reduced inverse
is called the reduced radius. The existing groups may be recombined to form two other dimensionless groups for substitution into the differential equation. The first is what could be called the square of the reduced inverse  . The second could be called the reduced central ion charge,
. The second could be called the reduced central ion charge,  (with a capital Z). Note that, though
(with a capital Z). Note that, though  is already dimensionless, without the substitution given below, the differential equation would still be dimensional.
is already dimensionless, without the substitution given below, the differential equation would still be dimensional.


 groups to eliminate
groups to eliminate  in favor of
in favor of  , then eliminate
, then eliminate  in favor of
in favor of  while carrying out the chain rule and substituting
while carrying out the chain rule and substituting  , then eliminate
, then eliminate 


 where
where  is the integer charge of the ion (1 for H, 2 for Mg etc.),
is the integer charge of the ion (1 for H, 2 for Mg etc.),  is the size or effective diameter of the ion in
is the size or effective diameter of the ion in  are constants with values of respectively 0.5085 and 0.3281 at 25 °C in water .
are constants with values of respectively 0.5085 and 0.3281 at 25 °C in water .

 is known as the limiting molar conductivity, K is an empirical constant and c is the electrolyte concentration. Limiting here means "at the limit of the infinite dilution").
Onsager's expression is
is known as the limiting molar conductivity, K is an empirical constant and c is the electrolyte concentration. Limiting here means "at the limit of the infinite dilution").
Onsager's expression is

 where
where
 is a notation for
is a notation for  is a
is a  is the number of species participating in the reaction,
is the number of species participating in the reaction, is the
is the  is the
is the  with
with  , where
, where  is
is

 to express the effect of electrostatic forces in an electrolyte on its thermodynamic state. Specifically, they split most of the
to express the effect of electrostatic forces in an electrolyte on its thermodynamic state. Specifically, they split most of the  where
where
 is
is  is
is  is
is  where
where
 is
is  is
is 
 which are useful further on.
which are useful further on.
 where
where
 indicates the classical part,
indicates the classical part, indicates the electric part.
indicates the electric part.


 , an assumption that the solvent is incompressible.
, an assumption that the solvent is incompressible.
 where
where  is
is 
 amounts to 20 atmospheres. Furthermore, they note that this level of pressure gives a relative volume change of 0.001. Therefore, they neglect change in volume of water due to electric pressure, writing
amounts to 20 atmospheres. Furthermore, they note that this level of pressure gives a relative volume change of 0.001. Therefore, they neglect change in volume of water due to electric pressure, writing
 and put
and put

 where
where
 is the number of particles of species i,
is the number of particles of species i, is the particle specific Gibbs free entropy of species i,
is the particle specific Gibbs free entropy of species i, is the
is the 
 may be derived from the functional dependence of the chemical potential of a component of an
may be derived from the functional dependence of the chemical potential of a component of an  where
where
 is the
is the  , where
, where  is the
is the  is the value of the scalar
is the value of the scalar  are altered from their bulk (overall average) values
are altered from their bulk (overall average) values  by the corresponding
by the corresponding  , where
, where 


 for
for  ) to create a linear differential equation. D&H say that this approximation holds at large distances between ions, which is the same as saying that the concentration is low. Lastly, they claim without proof that the addition of more terms in the expansion has little effect on the final solution. Thus
) to create a linear differential equation. D&H say that this approximation holds at large distances between ions, which is the same as saying that the concentration is low. Lastly, they claim without proof that the addition of more terms in the expansion has little effect on the final solution. Thus

 because the first summation is zero due to electroneutrality.
because the first summation is zero due to electroneutrality.
 . Also, let
. Also, let 


 is called the
is called the 
 is a positive constant):
is a positive constant):
 where
where  , beyond which no ions in the atmosphere may approach the (charge) center of the singled out ion. This radius may be due to the physical size of the ion itself, the sizes of the ions in the cloud, and any water molecules that surround the ions. Mathematically, they treat the singled out ion as a
, beyond which no ions in the atmosphere may approach the (charge) center of the singled out ion. This radius may be due to the physical size of the ion itself, the sizes of the ions in the cloud, and any water molecules that surround the ions. Mathematically, they treat the singled out ion as a 
 where
where  is a constant that represents the potential added by the ionic atmosphere. No justification for
is a constant that represents the potential added by the ionic atmosphere. No justification for 




