Misplaced Pages

In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface (two-dimensional manifold).

Definition

Suppose that c is a simple closed curve in a closed, orientable surface S. Let A be a tubular neighborhood of c. Then A is an annulus, homeomorphic to the Cartesian product of a circle and a unit interval I:

${\displaystyle c\subset A\cong S^{1}\times I.}$

Give A coordinates (s, t) where s is a complex number of the form ${\displaystyle e^{i\theta }}$ with ${\displaystyle \theta \in ,}$ and t ∈ .

Let f be the map from S to itself which is the identity outside of A and inside A we have

${\displaystyle f(s,t)=\left(se^{i2\pi t},t\right).}$

Then f is a Dehn twist about the curve c.

Dehn twists can also be defined on a non-orientable surface S, provided one starts with a 2-sided simple closed curve c on S.

Example

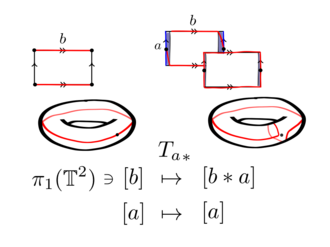
Consider the torus represented by a fundamental polygon with edges a and b

${\displaystyle \mathbb {T} ^{2}\cong \mathbb {R} ^{2}/\mathbb {Z} ^{2}.}$

Let a closed curve be the line along the edge a called ${\displaystyle \gamma _{a}}$.

Given the choice of gluing homeomorphism in the figure, a tubular neighborhood of the curve ${\displaystyle \gamma _{a}}$ will look like a band linked around a doughnut. This neighborhood is homeomorphic to an annulus, say

${\displaystyle a(0;0,1)=\{z\in \mathbb {C} :0<|z|<1\}}$

in the complex plane.

By extending to the torus the twisting map ${\displaystyle \left(e^{i\theta },t\right)\mapsto \left(e^{i\left(\theta +2\pi t\right)},t\right)}$ of the annulus, through the homeomorphisms of the annulus to an open cylinder to the neighborhood of ${\displaystyle \gamma _{a}}$, yields a Dehn twist of the torus by a.

${\displaystyle T_{a}:\mathbb {T} ^{2}\to \mathbb {T} ^{2}}$

This self homeomorphism acts on the closed curve along b. In the tubular neighborhood it takes the curve of b once along the curve of a.

A homeomorphism between topological spaces induces a natural isomorphism between their fundamental groups. Therefore one has an automorphism

${\displaystyle {T_{a}}_{\ast }:\pi _{1}\left(\mathbb {T} ^{2}\right)\to \pi _{1}\left(\mathbb {T} ^{2}\right):\mapsto \left}$

where are the homotopy classes of the closed curve x in the torus. Notice ${\displaystyle {T_{a}}_{\ast }()=}$ and ${\displaystyle {T_{a}}_{\ast }()=}$, where ${\displaystyle b*a}$ is the path travelled around b then a.

Mapping class group

It is a theorem of Max Dehn that maps of this form generate the mapping class group of isotopy classes of orientation-preserving homeomorphisms of any closed, oriented genus-${\displaystyle g}$ surface. W. B. R. Lickorish later rediscovered this result with a simpler proof and in addition showed that Dehn twists along ${\displaystyle 3g-1}$ explicit curves generate the mapping class group (this is called by the punning name "Lickorish twist theorem"); this number was later improved by Stephen P. Humphries to ${\displaystyle 2g+1}$, for ${\displaystyle g>1}$, which he showed was the minimal number.

Lickorish also obtained an analogous result for non-orientable surfaces, which require not only Dehn twists, but also "Y-homeomorphisms."

See also

• Fenchel–Nielsen coordinates
• Lantern relation

References

• Andrew J. Casson, Steven A Bleiler, Automorphisms of Surfaces After Nielsen and Thurston, Cambridge University Press, 1988. ISBN 0-521-34985-0.
• Stephen P. Humphries, "Generators for the mapping class group," in: Topology of low-dimensional manifolds (Proc. Second Sussex Conf., Chelwood Gate, 1977), pp. 44–47, Lecture Notes in Math., 722, Springer, Berlin, 1979. MR0547453
• W. B. R. Lickorish, "A representation of orientable combinatorial 3-manifolds." Ann. of Math. (2) 76 1962 531—540. MR0151948
• W. B. R. Lickorish, "A finite set of generators for the homotopy group of a 2-manifold", Proc. Cambridge Philos. Soc. 60 (1964), 769–778. MR0171269

• Geometric topology
• Homeomorphisms