
The Doomsday rule, Doomsday algorithm or Doomsday method is an algorithm of determination of the day of the week for a given date. It provides a perpetual calendar because the Gregorian calendar moves in cycles of 400 years. The algorithm for mental calculation was devised by John Conway in 1973, drawing inspiration from Lewis Carroll's perpetual calendar algorithm. It takes advantage of each year having a certain day of the week upon which certain easy-to-remember dates, called the doomsdays, fall; for example, the last day of February, April 4 (4/4), June 6 (6/6), August 8 (8/8), October 10 (10/10), and December 12 (12/12) all occur on the same day of the week in any year.
Applying the Doomsday algorithm involves three steps: determination of the anchor day for the century, calculation of the anchor day for the year from the one for the century, and selection of the closest date out of those that always fall on the doomsday, e.g., 4/4 and 6/6, and count of the number of days (modulo 7) between that date and the date in question to arrive at the day of the week. The technique applies to both the Gregorian calendar and the Julian calendar, although their doomsdays are usually different days of the week.
The algorithm is simple enough that it can be computed mentally. Conway could usually give the correct answer in under two seconds. To improve his speed, he practiced his calendrical calculations on his computer, which was programmed to quiz him with random dates every time he logged on.
Anchor days for some contemporary years
Doomsday's anchor day for the current year in the Gregorian calendar (2024) is Thursday. For some other contemporary years:
| Sunday | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday |
|---|---|---|---|---|---|---|
| 1796 | 1797 | 1798 | 1799 | 1800 | 1801 | |
| 1802 | 1803 | 1804 | 1805 | 1806 | 1807 | |
| 1808 | 1809 | 1810 | 1811 | 1812 | ||
| 1813 | 1814 | 1815 | 1816 | 1817 | 1818 | |
| 1819 | 1820 | 1821 | 1822 | 1823 | ||
| 1824 | 1825 | 1826 | 1827 | 1828 | 1829 | |
| 1830 | 1831 | 1832 | 1833 | 1834 | 1835 | |
| 1836 | 1837 | 1838 | 1839 | 1840 | ||
| 1841 | 1842 | 1843 | 1844 | 1845 | 1846 | |
| 1847 | 1848 | 1849 | 1850 | 1851 | ||
| 1852 | 1853 | 1854 | 1855 | 1856 | 1857 | |
| 1858 | 1859 | 1860 | 1861 | 1862 | 1863 | |
| 1864 | 1865 | 1866 | 1867 | 1868 | ||
| 1869 | 1870 | 1871 | 1872 | 1873 | 1874 | |
| 1875 | 1876 | 1877 | 1878 | 1879 | ||
| 1880 | 1881 | 1882 | 1883 | 1884 | 1885 | |
| 1886 | 1887 | 1888 | 1889 | 1890 | 1891 | |
| 1892 | 1893 | 1894 | 1895 | 1896 | ||
| 1897 | 1898 | 1899 | 1900 | 1901 | 1902 | 1903 |
| 1904 | 1905 | 1906 | 1907 | 1908 | ||
| 1909 | 1910 | 1911 | 1912 | 1913 | 1914 | |
| 1915 | 1916 | 1917 | 1918 | 1919 | ||
| 1920 | 1921 | 1922 | 1923 | 1924 | 1925 | |
| 1926 | 1927 | 1928 | 1929 | 1930 | 1931 | |
| 1932 | 1933 | 1934 | 1935 | 1936 | ||
| 1937 | 1938 | 1939 | 1940 | 1941 | 1942 | |
| 1943 | 1944 | 1945 | 1946 | 1947 | ||
| 1948 | 1949 | 1950 | 1951 | 1952 | 1953 | |
| 1954 | 1955 | 1956 | 1957 | 1958 | 1959 | |
| 1960 | 1961 | 1962 | 1963 | 1964 | ||
| 1965 | 1966 | 1967 | 1968 | 1969 | 1970 | |
| 1971 | 1972 | 1973 | 1974 | 1975 | ||
| 1976 | 1977 | 1978 | 1979 | 1980 | 1981 | |
| 1982 | 1983 | 1984 | 1985 | 1986 | 1987 | |
| 1988 | 1989 | 1990 | 1991 | 1992 | ||
| 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | |
| 1999 | 2000 | 2001 | 2002 | 2003 | ||
| 2004 | 2005 | 2006 | 2007 | 2008 | 2009 | |
| 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | |
| 2016 | 2017 | 2018 | 2019 | 2020 | ||
| 2021 | 2022 | 2023 | 2024 | 2025 | 2026 | |
| 2027 | 2028 | 2029 | 2030 | 2031 | ||
| 2032 | 2033 | 2034 | 2035 | 2036 | 2037 | |
| 2038 | 2039 | 2040 | 2041 | 2042 | 2043 | |
| 2044 | 2045 | 2046 | 2047 | 2048 | ||
| 2049 | 2050 | 2051 | 2052 | 2053 | 2054 | |
| 2055 | 2056 | 2057 | 2058 | 2059 | ||
| 2060 | 2061 | 2062 | 2063 | 2064 | 2065 | |
| 2066 | 2067 | 2068 | 2069 | 2070 | 2071 | |
| 2072 | 2073 | 2074 | 2075 | 2076 | ||
| 2077 | 2078 | 2079 | 2080 | 2081 | 2082 | |
| 2083 | 2084 | 2085 | 2086 | 2087 | ||
| 2088 | 2089 | 2090 | 2091 | 2092 | 2093 | |
| 2094 | 2095 | 2096 | 2097 | 2098 | 2099 | |
| 2100 | 2101 | 2102 | 2103 | 2104 | 2105 |
The table is filled in horizontally, skipping one column for each leap year. This table cycles every 28 years, except in the Gregorian calendar on years that are a multiple of 100 (such as 1800, 1900, and 2100 which are not leap years) that are not also a multiple of 400 (like 2000 which is still a leap year). The full cycle is 28 years (1,461 weeks) in the Julian calendar and 400 years (20,871 weeks) in the Gregorian calendar.
Memorable dates that always land on Doomsday
One can find the day of the week of a given calendar date by using a nearby doomsday as a reference point. To help with this, the following is a list of easy-to-remember dates for each month that always land on the doomsday.
The last day of February is always a doomsday. For January, January 3 is a doomsday during common years and January 4 a doomsday during leap years, which can be remembered as "the 3rd during 3 years in 4, and the 4th in the 4th year". For March, one can remember either Pi Day or "March 0", the latter referring to the day before March 1, i.e. the last day of February.
For the months April through December, the even numbered months are covered by the double dates 4/4, 6/6, 8/8, 10/10, and 12/12, all of which fall on the doomsday. The odd numbered months can be remembered with the mnemonic "I work from 9 to 5 at the 7-11", i.e., 9/5, 7/11, and also 5/9 and 11/7, are all doomsdays (this is true for both the Day/Month and Month/Day conventions).
Several well-known dates, such as Independence Day in United States, Boxing Day, and Valentine's Day in common years, also fall on doomsdays every year. The chart below includes only the mnemonics covered in the sources listed.
| Month | Memorable date | Month/Day | Mnemonic | Complete list of days |
|---|---|---|---|---|
| January | January 3 (common years), January 4 (leap years) |
1/3 OR 1/4 (1/31 OR 1/32) | the 3rd 3 years in 4 and the 4th in the 4th (or: last day of January, pretending leap years have a January 32nd) | 3, 10, 17, 24, 31 OR 4, 11, 18, 25, 32 |
| February | February 28 (common years), February 29 (leap years) | 2/0 OR 2/1 (2/28 OR 2/29) | last day of January, pretending leap years have a January 32nd (or: last day of February) | 0, 7, 14, 21, 28 OR 1, 8, 15, 22, 29 |
| March | "March 0," March 14 | 3/0 AND 3/14 | last day of February, Pi Day | 0, 7, 14, 21, 28 |
| April | April 4 | 4/4 | 4/4, 6/6, 8/8, 10/10, 12/12 | 4, 11, 18, 25 |
| May | May 9 | 5/9 | 9-to-5 at 7-11 | 2, 9, 16, 23, 30 |
| June | June 6 | 6/6 | 4/4, 6/6, 8/8, 10/10, 12/12 | 6, 13, 20, 27 |
| July | July 11 | 7/11 | 9-to-5 at 7-11 | 4, 11, 18, 25 |
| August | August 8 | 8/8 | 4/4, 6/6, 8/8, 10/10, 12/12 | 1, 8, 15, 22, 29 |
| September | September 5 | 9/5 | 9-to-5 at 7-11 | 5, 12, 19, 26 |
| October | October 10 | 10/10 | 4/4, 6/6, 8/8, 10/10, 12/12 | 3, 10, 17, 24, 31 |
| November | November 7 | 11/7 | 9-to-5 at 7-11 | 7, 14, 21, 28 |
| December | December 12 | 12/12 | 4/4, 6/6, 8/8, 10/10, 12/12 | 5, 12, 19, 26 |
Since the doomsday for a particular year is directly related to weekdays of dates in the period from March through February of the next year, common years and leap years have to be distinguished for January and February of the same year.
Example
To find which day of the week Christmas Day of 2021 is, proceed as follows: in the year 2021, doomsday is on Sunday. Since December 12 is a doomsday, December 25, being thirteen days afterwards (two weeks less a day), fell on a Saturday. Christmas Day is always the day of the week before doomsday. In addition, July 4 (U.S. Independence Day) is always on the same day of the week as a doomsday, as are Halloween (October 31), Pi Day (March 14), and December 26 (Boxing Day).
Mnemonic weekday names
Since this algorithm involves treating days of the week like numbers modulo 7, John Conway suggested thinking of the days of the week as "Noneday" or "Sansday" (for Sunday), "Oneday", "Twosday", "Treblesday", "Foursday", "Fiveday", and "Six-a-day" in order to recall the number-weekday relation without needing to count them out in one's head.
| day of week | Index number |
Mnemonic |
|---|---|---|
| Sunday | 0 | Noneday or Sansday |
| Monday | 1 | Oneday |
| Tuesday | 2 | Twosday |
| Wednesday | 3 | Treblesday |
| Thursday | 4 | Foursday |
| Friday | 5 | Fiveday |
| Saturday | 6 | Six-a-day |
There are some languages, such as Slavic languages, Chinese, Estonian, Greek, Portuguese, Galician and Hebrew, that base some of the names of the week days in their positional order. The Slavic, Chinese, and Estonian agree with the table above; the other languages mentioned count from Sunday as day one.
Finding a year's anchor day
First take the anchor day for the century. For the purposes of the doomsday rule, a century starts with '00 and ends with '99. The following table shows the anchor day of centuries 1600–1699, 1700–1799, 1800–1899, 1900–1999, 2000–2099, 2100–2199 and 2200–2299.
| Century | Anchor day | Mnemonic | Index (day of week) |
|---|---|---|---|
| 1600–1699 | Tuesday | — | 2 (Twoday) |
| 1700–1799 | Sunday | — | 0 (Noneday) |
| 1800–1899 | Friday | — | 5 (Fiveday) |
| 1900–1999 | Wednesday | We-in-dis-day (most living people were born in that century) |
3 (Treblesday) |
| 2000–2099 | Tuesday | Y-Tue-K or Twos-day (Y2K was at the head of this century) |
2 (Twosday) |
| 2100–2199 | Sunday | Twenty-one-day is Sunday (2100 is the start of the next century) |
0 (Noneday) |
| 2200–2299 | Friday | — | 5 (Fiveday) |
For the Gregorian calendar:
- Mathematical formula
- 5 × (c mod 4) mod 7 + Tuesday = anchor.
- Algorithmic
- Let r = c mod 4
- if r = 0 then anchor = Tuesday
- if r = 1 then anchor = Sunday
- if r = 2 then anchor = Friday
- if r = 3 then anchor = Wednesday
For the Julian calendar:
- 6c mod 7 + Sunday = anchor.
Note: .
Next, find the year's anchor day. To accomplish that according to Conway:
- Divide the year's last two digits (call this y) by 12 and let a be the floor of the quotient.
- Let b be the remainder of the same quotient.
- Divide that remainder by 4 and let c be the floor of the quotient.
- Let d be the sum of the three numbers (d = a + b + c). (It is again possible here to divide by seven and take the remainder. This number is equivalent, as it must be, to y plus the floor of y divided by four.)
- Count forward the specified number of days (d or the remainder of d/7) from the anchor day to get the year's one.
For the twentieth-century year 1966, for example:
As described in bullet 4, above, this is equivalent to:
So doomsday in 1966 fell on Monday.
Similarly, doomsday in 2005 is on a Monday:
Why it works

The doomsday's anchor day calculation is effectively calculating the number of days between any given date in the base year and the same date in the current year, then taking the remainder modulo 7. When both dates come after the leap day (if any), the difference is just 365y + y/4 (rounded down). But 365 equals 52 × 7 + 1, so after taking the remainder we get just
This gives a simpler formula if one is comfortable dividing large values of y by both 4 and 7. For example, we can compute
which gives the same answer as in the example above.
Where 12 comes in is that the pattern of almost repeats every 12 years. After 12 years, we get . If we replace y by y mod 12, we are throwing this extra day away; but adding back in compensates for this error, giving the final formula.
For calculating the Gregorian anchor day of a century: three “common centuries” (each having 24 leap years) are followed by a “leap century” (having 25 leap years). A common century moves the doomsday forward by
days (equivalent to two days back). A leap century moves the doomsday forward by 6 days (equivalent to one day back).
So c centuries move the doomsday forward by
- ,
but this is equivalent to
- .
Four centuries move the doomsday forward by
- ;
so four centuries form a cycle that leaves the doomsday unchanged (and hence the “mod 4” in the century formula).
The "odd + 11" method
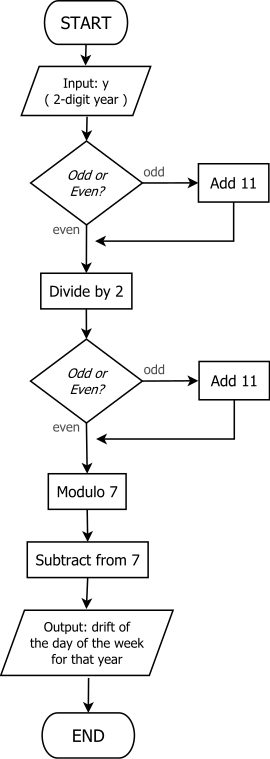
A simpler method for finding the year's anchor day was discovered in 2010 by Chamberlain Fong and Michael K. Walters, and described in their paper submitted to the 7th International Congress on Industrial and Applied Mathematics (2011). Called the "odd + 11" method, it is equivalent to computing
- .
It is well suited to mental calculation, because it requires no division by 4 (or 12), and the procedure is easy to remember because of its repeated use of the "odd + 11" rule. Furthermore, addition by 11 is very easy to perform mentally in base-10 arithmetic.
Extending this to get the anchor day, the procedure is often described as accumulating a running total T in six steps, as follows:
- Let T be the year's last two digits.
- If T is odd, add 11.
- Now let T = T/2.
- If T is odd, add 11.
- Now let T = 7 − (T mod 7).
- Count forward T days from the century's anchor day to get the year's anchor day.
Applying this method to the year 2005, for example, the steps as outlined would be:
- T = 5
- T = 5 + 11 = 16 (adding 11 because T is odd)
- T = 16/2 = 8
- T = 8 (do nothing since T is even)
- T = 7 − (8 mod 7) = 7 − 1 = 6
- Doomsday for 2005 = 6 + Tuesday = Monday
The explicit formula for the odd+11 method is:
- .
Although this expression looks daunting and complicated, it is actually simple because of a common subexpression y + 11(y mod 2)/2 that only needs to be calculated once.
Anytime adding 11 is needed, subtracting 17 yields equivalent results. While subtracting 17 may seem more difficult to mentally perform than adding 11, there are cases where subtracting 17 is easier, especially when the number is a two-digit number that ends in 7 (such as 17, 27, 37, ..., 77, 87, and 97).
Correspondence with dominical letter
Doomsday is related to the dominical letter of the year as follows.
| Doomsday | Dominical letter | |
|---|---|---|
| Common year | Leap year | |
| Sunday | C | DC |
| Monday | B | CB |
| Tuesday | A | BA |
| Wednesday | G | AG |
| Thursday | F | GF |
| Friday | E | FE |
| Saturday | D | ED |
Look up the table below for the dominical letter (DL).
| Hundreds of Years | D L |
Remaining Year Digits | # | ||||
|---|---|---|---|---|---|---|---|
| Julian (r ÷ 7) |
Gregorian (r ÷ 4) | ||||||
| r5 19 | 16 20 r0 | A | 00 06 17 23 | 28 34 45 51 | 56 62 73 79 | 84 90 | 0 |
| r4 18 | 15 19 r3 | G | 01 07 12 18 | 29 35 40 46 | 57 63 68 74 | 85 91 96 | 1 |
| r3 17 | N/A | F | 02 13 19 24 | 30 41 47 52 | 58 69 75 80 | 86 97 | 2 |
| r2 16 | 18 22 r2 | E | 03 08 14 25 | 31 36 42 53 | 59 64 70 81 | 87 92 98 | 3 |
| r1 15 | N/A | D | 09 15 20 26 | 37 43 48 54 | 65 71 76 82 | 93 99 | 4 |
| r0 14 | 17 21 r1 | C | 04 10 21 27 | 32 38 49 55 | 60 66 77 83 | 88 94 | 5 |
| r6 13 | N/A | B | 05 11 16 22 | 33 39 44 50 | 61 67 72 78 | 89 95 | 6 |
For the year 2024, the dominical letter is BA + 2 = GF.
Overview of all Doomsdays
| Month | Dates | Week numbers * |
|---|---|---|
| January (common years) | 3, 10, 17, 24, 31 | 1–5 |
| January (leap years) | 4, 11, 18, 25 | 1–4 |
| February (common years) | 7, 14, 21, 28 | 6–9 |
| February (leap years) | 1, 8, 15, 22, 29 | 5–9 |
| March | 7, 14, 21, 28 | 10–13 |
| April | 4, 11, 18, 25 | 14–17 |
| May | 2, 9, 16, 23, 30 | 18–22 |
| June | 6, 13, 20, 27 | 23–26 |
| July | 4, 11, 18, 25 | 27–30 |
| August | 1, 8, 15, 22, 29 | 31–35 |
| September | 5, 12, 19, 26 | 36–39 |
| October | 3, 10, 17, 24, 31 | 40–44 |
| November | 7, 14, 21, 28 | 45–48 |
| December | 5, 12, 19, 26 | 49–52 |
* In leap years the nth doomsday is in ISO week n. In common years the day after the nth doomsday is in week n. Thus in a common year the week number on the doomsday itself is one less if it is a Sunday, i.e. in a common year starting on Friday (such as 2010, 2021, & 2027).
Computer formula for the anchor day of a year
For computer use, the following formulas for the anchor day of a year are convenient.
For the Gregorian calendar:
For example, the doomsday 2009 is Saturday under the Gregorian calendar (the currently accepted calendar), since
As another example, the doomsday 1946 is Thursday, since
For the Julian calendar:
The formulas apply also for the proleptic Gregorian calendar and the proleptic Julian calendar. They use the floor function and astronomical year numbering for years BC.
For comparison, see the calculation of a Julian day number.
400-year cycle of anchor days
| Julian centuries | -1600J -900J -200J 500J 1200J 1900J 2600J 3300J |
-1500J -800J -100J 600J 1300J 2000J 2700J 3400J |
-1400J -700J 0J 700J 1400J 2100J 2800J 3500J |
-1300J -600J 100J 800J 1500J 2200J 2900J 3600J |
-1200J -500J 200J 900J 1600J 2300J 3000J 3700J |
-1100J -400J 300J 1000J 1700J 2400J 3100J 3800J |
-1000J -300J 400J 1100J 1800J 2500J 3200J 3900J | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Gregorian centuries Years |
-1600 -1200 -800 -400 0 400 800 1200 1600 2000 2400 2800 3200 3600 |
-1500 -1100 -700 -300 100 500 900 1300 1700 2100 2500 2900 3300 3700 |
-1400 -1000 -600 -200 200 600 1000 1400 1800 2200 2600 3000 3400 3800 |
-1300 -900 -500 -100 300 700 1100 1500 1900 2300 2700 3100 3500 3900 | ||||||
| 00 | 28 | 56 | 84 | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. |
| 01 | 29 | 57 | 85 | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. |
| 02 | 30 | 58 | 86 | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. |
| 03 | 31 | 59 | 87 | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. |
| 04 | 32 | 60 | 88 | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. |
| 05 | 33 | 61 | 89 | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. |
| 06 | 34 | 62 | 90 | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. |
| 07 | 35 | 63 | 91 | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. |
| 08 | 36 | 64 | 92 | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. |
| 09 | 37 | 65 | 93 | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. |
| 10 | 38 | 66 | 94 | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. |
| 11 | 39 | 67 | 95 | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. |
| 12 | 40 | 68 | 96 | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. |
| 13 | 41 | 69 | 97 | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. |
| 14 | 42 | 70 | 98 | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. |
| 15 | 43 | 71 | 99 | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. |
| 16 | 44 | 72 | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. | |
| 17 | 45 | 73 | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. | |
| 18 | 46 | 74 | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. | |
| 19 | 47 | 75 | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. | |
| 20 | 48 | 76 | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. | |
| 21 | 49 | 77 | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. | |
| 22 | 50 | 78 | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. | |
| 23 | 51 | 79 | Tue. | Mon. | Sun. | Sat. | Fri. | Thu. | Wed. | |
| 24 | 52 | 80 | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. | Fri. | |
| 25 | 53 | 81 | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. | Sat. | |
| 26 | 54 | 82 | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. | Sun. | |
| 27 | 55 | 83 | Sun. | Sat. | Fri. | Thu. | Wed. | Tue. | Mon. | |
Since in the Gregorian calendar there are 146,097 days, or exactly 20,871 seven-day weeks, in 400 years, the anchor day repeats every four centuries. For example, the anchor day of 1700–1799 is the same as the anchor day of 2100–2199, i.e. Sunday.
The full 400-year cycle of doomsdays is given in the adjacent table. The centuries are for the Gregorian and proleptic Gregorian calendar, unless marked with a J for Julian. The Gregorian leap years are highlighted.
Negative years use astronomical year numbering. Year 25BC is −24, shown in the column of −100J (proleptic Julian) or −100 (proleptic Gregorian), at the row 76.
| Sunday | Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Total | |
|---|---|---|---|---|---|---|---|---|
| Non-leap years | 43 | 43 | 43 | 43 | 44 | 43 | 44 | 303 |
| Leap years | 13 | 15 | 13 | 15 | 13 | 14 | 14 | 97 |
| Total | 56 | 58 | 56 | 58 | 57 | 57 | 58 | 400 |
A leap year with Monday as doomsday means that Sunday is one of 97 days skipped in the 400-year sequence. Thus the total number of years with Sunday as doomsday is 71 minus the number of leap years with Monday as doomsday, etc. Since Monday as doomsday is skipped across February 29, 2000, and the pattern of leap days is symmetric about that leap day, the frequencies of doomsdays per weekday (adding common and leap years) are symmetric about Monday. The frequencies of doomsdays of leap years per weekday are symmetric about the doomsday of 2000, Tuesday.
The frequency of a particular date being on a particular weekday can easily be derived from the above (for a date from January 1 – February 28, relate it to the doomsday of the previous year).
For example, February 28 is one day after doomsday of the previous year, so it is 58 times each on Tuesday, Thursday and Sunday, etc. February 29 is doomsday of a leap year, so it is 15 times each on Monday and Wednesday, etc.
28-year cycle
Regarding the frequency of doomsdays in a Julian 28-year cycle, there are 1 leap year and 3 common years for every weekday, the latter 6, 17 and 23 years after the former (so with intervals of 6, 11, 6, and 5 years; not evenly distributed because after 12 years the day is skipped in the sequence of doomsdays). The same cycle applies for any given date from March 1 falling on a particular weekday.
For any given date up to February 28 falling on a particular weekday, the 3 common years are 5, 11, and 22 years after the leap year, so with intervals of 5, 6, 11, and 6 years. Thus the cycle is the same, but with the 5-year interval after instead of before the leap year.
Thus, for any date except February 29, the intervals between common years falling on a particular weekday are 6, 11, 11. See e.g. at the bottom of the page Common year starting on Monday the years in the range 1906–2091.
For February 29 falling on a particular weekday, there is just one in every 28 years, and it is of course a leap year.
Julian calendar
The Gregorian calendar is currently accurately lining up with astronomical events such as solstices. In 1582 this modification of the Julian calendar was first instituted. In order to correct for calendar drift, 10 days were skipped, so doomsday moved back 10 days (i.e. 3 days): Thursday, October 4 (Julian, doomsday is Wednesday) was followed by Friday, October 15 (Gregorian, doomsday is Sunday). The table includes Julian calendar years, but the algorithm is for the Gregorian and proleptic Gregorian calendar only.
Note that the Gregorian calendar was not adopted simultaneously in all countries, so for many centuries, different regions used different dates for the same day.
Full examples
Example 1 (1985)
Suppose we want to know the day of the week of September 18, 1985. We begin with the century's anchor day, Wednesday. To this, add a, b, and c above:
- a is the floor of 85/12, which is 7.
- b is 85 mod 12, which is 1.
- c is the floor of b/4, which is 0.
This yields a + b + c = 8. Counting 8 days from Wednesday, we reach Thursday, which is the doomsday in 1985. (Using numbers: In modulo 7 arithmetic, 8 is congruent to 1. Because the century's anchor day is Wednesday (index 3), and 3 + 1 = 4, doomsday in 1985 was Thursday (index 4).) We now compare September 18 to a nearby doomsday, September 5. We see that the 18th is 13 past a doomsday, i.e. one day less than two weeks. Hence, the 18th was a Wednesday (the day preceding Thursday). (Using numbers: In modulo 7 arithmetic, 13 is congruent to 6 or, more succinctly, −1. Thus, we take one away from the doomsday, Thursday, to find that September 18, 1985, was a Wednesday.)
Example 2 (other centuries)
Suppose that we want to find the day of week that the American Civil War broke out at Fort Sumter, which was April 12, 1861. The anchor day for the century was 94 days after Tuesday, or, in other words, Friday (calculated as 18 × 5 + ⌊18/4⌋; or just look at the chart, above, which lists the century's anchor days). The digits 61 gave a displacement of six days so doomsday was Thursday. Therefore, April 4 was Thursday so April 12, eight days later, was a Friday.
See also
- Ordinal date
- Computus – Gauss algorithm for Easter date calculation
- Zeller's congruence – An algorithm (1882) to calculate the day of the week for any Julian or Gregorian calendar date.
- Mental calculation
References
- John Horton Conway, "Tomorrow is the Day After Doomsday" (PDF). Eureka. October 1973. p. 28-32.
- Richard Guy, John Horton Conway, Elwyn Berlekamp : "Winning Ways: For Your Mathematical Plays, Volume. 2: Games in Particular", pages 795–797, Academic Press, London, 1982, ISBN 0-12-091102-7.
- Lewis Carroll, "To Find the Day of the Week for Any Given Date", Nature, March 31, 1887. doi:10.1038/035517a0
- Martin Gardner, The Universe in a Handkerchief: Lewis Carroll's Mathematical Recreations, Games, Puzzles, and Word Plays, pages 24–26, Springer-Verlag, 1996.
- "What Day is Doomsday". Mathematics Awareness Month. April 2014.
- Alpert, Mark (April 1, 1999). "Not Just Fun and Games". Scientific American. Retrieved April 18, 2024.
- ^ Torrence, Bruce; Torrence, Eve. "John H. Conway - Doomsday, part 1". YouTube. Mathematical Association of America. Archived from the original on December 21, 2021. Retrieved April 14, 2020.
- "The Doomsday Algorithm - Numberphile". YouTube. Retrieved July 9, 2023.
- ^ Limeback, Rudy (January 3, 2017). "Doomsday Algorithm". Retrieved May 27, 2017.
- "On what day of the week is Christmas? Use the Doomsday Rule". The Irish Times. Retrieved July 20, 2022.
- John Horton Conway, "Tomorrow is the Day After Doomsday" (PDF). Eureka. October 1973. p. 29-30.
Each ordinary year has its Doomsday 1 day later than the previous year, and each leap year 2 days later. It follows that within any given century a dozen years advances Doomsday by 12 + 3 = 15 days = 1 day. ('A dozen years is but a day.') So we add to the Doomsday for the century year the number of dozens of years thereafter, the remainder, and the number of fours in the remainder.
- ^ Chamberlain Fong, Michael K. Walters: "Methods for Accelerating Conway's Doomsday Algorithm (part 2)", 7th International Congress on Industrial and Applied Mathematics (2011).
External links
- Encyclopedia of Weekday Calculation by Hans-Christian Solka, 2010
- World records for mentally calculating the day of the week in the Gregorian Calendar
- National records for finding Calendar Dates
- World Ranking of Memoriad Mental Calendar Dates (all competitions combined)
- Doomsday Algorithm
- Finding the Day of the Week
- Poem explaining the Doomsday rule at the Wayback Machine (archived October 18, 2006)
- Doomsday Calculator at timeanddate
| Gregorian year types per leap cycle by Dominical letter (DL) and Doomsday (DD) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Source: Robert van Gent (2017). "The Mathematics of the ISO 8601 Calendar". Utrecht University, Department of Mathematics. Retrieved July 20, 2017. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 .
.






 almost repeats every 12 years. After 12 years, we get
almost repeats every 12 years. After 12 years, we get  . If we replace y by y mod 12, we are throwing this extra day away; but adding back in
. If we replace y by y mod 12, we are throwing this extra day away; but adding back in  compensates for this error, giving the final formula.
compensates for this error, giving the final formula.

 ,
, .
. ;
; .
. .
.


