This articles gives the crystalline structures of the elements of the periodic table which have been produced in bulk at STP and at their melting point (while still solid) and predictions of the crystalline structures of the rest of the elements.
Standard temperature and pressure
The following table gives the crystalline structure of the most thermodynamically stable form(s) for elements that are solid at standard temperature and pressure. Each element is shaded by a color representing its respective Bravais lattice, except that all orthorhombic lattices are grouped together.
| Crystal structure of elements in the periodic table at standard temperature and pressure | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 H |
2 He | ||||||||||||||||||
| 3 Li W |
4 Be Mg |
5 B β-B |
6 C g-C |
7 N |
8 O |
9 F |
10 Ne | ||||||||||||
| 11 Na W |
12 Mg Mg |
13 Al Cu |
14 Si d-C |
15 P b-P |
16 S α-S |
17 Cl |
18 Ar | ||||||||||||
| 19 K W |
20 Ca Cu |
21 Sc Mg |
22 Ti Mg |
23 V W |
24 Cr W |
25 Mn α-Mn |
26 Fe W |
27 Co Mg |
28 Ni Cu |
29 Cu Cu |
30 Zn Mg |
31 Ga α-Ga |
32 Ge d-C |
33 As α-As |
34 Se γ-Se |
35 Br |
36 Kr | ||
| 37 Rb W |
38 Sr Cu |
39 Y Mg |
40 Zr Mg |
41 Nb W |
42 Mo W |
43 Tc Mg |
44 Ru Mg |
45 Rh Cu |
46 Pd Cu |
47 Ag Cu |
48 Cd Mg |
49 In In |
50 Sn β-Sn |
51 Sb α-As |
52 Te γ-Se |
53 I Cl |
54 Xe | ||
| 55 Cs W |
56 Ba W |
71 Lu Mg |
72 Hf Mg |
73 Ta W |
74 W W |
75 Re Mg |
76 Os Mg |
77 Ir Cu |
78 Pt Cu |
79 Au Cu |
80 Hg |
81 Tl Mg |
82 Pb Cu |
83 Bi α-As |
84 Po α-Po |
85 At |
86 Rn | ||
| 87 Fr |
88 Ra W |
103 Lr |
104 Rf |
105 Db |
106 Sg |
107 Bh |
108 Hs |
109 Mt |
110 Ds |
111 Rg |
112 Cn |
113 Nh |
114 Fl |
115 Mc |
116 Lv |
117 Ts |
118 Og | ||
| 57 La α-La |
58 Ce α-La |
59 Pr α-La |
60 Nd α-La |
61 Pm α-La |
62 Sm α-Sm |
63 Eu W |
64 Gd Mg |
65 Tb Mg |
66 Dy Mg |
67 Ho Mg |
68 Er Mg |
69 Tm Mg |
70 Yb Cu | ||||||
| 89 Ac Cu |
90 Th Cu |
91 Pa α-Pa |
92 U α-U |
93 Np α-Np |
94 Pu α-Pu |
95 Am α-La |
96 Cm α-La |
97 Bk α-La |
98 Cf α-La |
99 Es Cu |
100 Fm |
101 Md |
102 No | ||||||
| Legend: |
|---|
| Primitive monoclinic structures: α-Pu |
| Orthorhombic structures: b-P, α-Ga, Cl, α-U, α-S, α-Np |
| Body-centered tetragonal structures: In, β-Sn, α-Pa |
| Rhombohedral structures: β-B, α-As, α-Sm |
| Hexagonal structures: Mg, α-La, g-C, γ-Se |
| Primitive cubic structures: α-Po |
| Body-centered cubic structures: W, α-Mn |
| Face-centered cubic structures: d-C, Cu |
| Not solid at standard temperature and pressure or uncertain |
Melting point and standard pressure
The following table gives the most stable crystalline structure of each element at its melting point at atmospheric pressure (H, He, N, O, F, Ne, Cl, Ar, Kr, Xe, and Rn are gases at STP; Br and Hg are liquids at STP.) Note that helium does not have a melting point at atmospheric pressure, but it adopts a magnesium-type hexagonal close-packed structure under high pressure.
| Crystal structures of elements at their melting points at atmospheric pressure | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 H 13 K Mg |
2 He * | ||||||||||||||||||
| 3 Li 453 K W |
4 Be 1560 K W |
5 B 2349 K β-B |
6 C 3800 K g-C |
7 N 63 K β-N |
8 O 54 K γ-O |
9 F 53 K γ-O |
10 Ne 24 K Cu | ||||||||||||
| 11 Na 370 K W |
12 Mg 923 K Mg |
13 Al 933 K Cu |
14 Si 1687 K d-C |
15 P 883 K b-P |
16 S 393 K β-S |
17 Cl 171 K Cl |
18 Ar 83 K Cu | ||||||||||||
| 19 K 336 K W |
20 Ca 1115 K W |
21 Sc 1814 K W |
22 Ti 1941 K W |
23 V 2183 K W |
24 Cr 2180 K W |
25 Mn 1519 K W |
26 Fe 1811 K W |
27 Co 1768 K Cu |
28 Ni 1728 K Cu |
29 Cu 1357 K Cu |
30 Zn 692 K Mg |
31 Ga 302 K α-Ga |
32 Ge 1211 K d-C |
33 As 1090 K b-P |
34 Se 494 K γ-Se |
35 Br 265 K Cl |
36 Kr 115 K Cu | ||
| 37 Rb 312 K W |
38 Sr 1050 K W |
39 Y 1799 K W |
40 Zr 2128 K W |
41 Nb 2750 K W |
42 Mo 2896 K W |
43 Tc 2430 K Mg |
44 Ru 2607 K Mg |
45 Rh 2237 K Cu |
46 Pd 1828 K Cu |
47 Ag 1234 K Cu |
48 Cd 594 K Mg |
49 In 429 K In |
50 Sn 505 K β-Sn |
51 Sb 903 K α-As |
52 Te 722 K γ-Se |
53 I 386 K Cl |
54 Xe 161 K Cu | ||
| 55 Cs 301 K W |
56 Ba 1000 K W |
71 Lu 1925 K Mg |
72 Hf 2506 K W |
73 Ta 3290 K W |
74 W 3695 K W |
75 Re 3459 K Mg |
76 Os 3306 K Mg |
77 Ir 2719 K Cu |
78 Pt 2041 K Cu |
79 Au 1337 K Cu |
80 Hg 234 K α-Hg |
81 Tl 557 K W |
82 Pb 600 K Cu |
83 Bi 544 K α-As |
84 Po 527 K β-Po |
85 At 575 K? ? |
86 Rn 202 K ? | ||
| 87 Fr 281 K? ? |
88 Ra 973 K W |
103 Lr 1900 K? ? |
104 Rf ? |
105 Db ? |
106 Sg ? |
107 Bh ? |
108 Hs ? |
109 Mt ? |
110 Ds ? |
111 Rg ? |
112 Cn ? |
113 Nh ? |
114 Fl ? |
115 Mc ? |
116 Lv ? |
117 Ts ? |
118 Og ? | ||
| 57 La 1193 K W |
58 Ce 1068 K W |
59 Pr 1208 K W |
60 Nd 1297 K W |
61 Pm 1315 K W |
62 Sm 1345 K W |
63 Eu 1099 K W |
64 Gd 1585 K W |
65 Tb 1629 K W |
66 Dy 1680 K W |
67 Ho 1734 K Mg |
68 Er 1802 K Mg |
69 Tm 1818 K Mg |
70 Yb 1097 K W | ||||||
| 89 Ac 1323 K Cu |
90 Th 2115 K W |
91 Pa 1841 K W |
92 U 1405 K W |
93 Np 917 K W |
94 Pu 912 K W |
95 Am 1449 K W |
96 Cm 1613 K Cu |
97 Bk 1259 K Cu |
98 Cf 1173 K Cu |
99 Es 1133 K Cu |
100 Fm 1800 K? ? |
101 Md 1100 K? ? |
102 No 1100 K? ? | ||||||
| Legend: |
|---|
| Primitive monoclinic structures: β-S |
| Orthorhombic structures: b-P, α-S, Cl, α-Ga |
| Body-centered tetragonal structures: In, β-Sn |
| Rhombohedral structures: β-B, α-As, α-Hg, α-Po |
| Primitive Hexagonal structures: Mg, g-C, β-N, γ-Se |
| Primitive cubic structure: γ-O |
| Body-centered cubic structure: W |
| Face-centered cubic structures: Cu, d-C |
| unknown or uncertain |
Predicted structures
The following table give predictions for the crystalline structure of elements 85–87, 100–113 and 118; all but radon have not been produced in bulk. Most probably Cn and Fl would be liquids at STP (ignoring radioactive self-heating concerns). Calculations have difficulty replicating the experimentally known bcc structures of the stable alkali metals, and the same problem affects Fr; nonetheless, it is probably also BCC. The latest predictions for Fl could not distinguish between FCC and HCP structures, which were predicted to be close in energy. No predictions are available for elements 115–117.
| Predicted crystal structures of highly unstable elements | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 H |
2 He | ||||||||||||||||||
| 3 Li |
4 Be |
5 B |
6 C |
7 N |
8 O |
9 F |
10 Ne | ||||||||||||
| 11 Na |
12 Mg |
13 Al |
14 Si |
15 P |
16 S |
17 Cl |
18 Ar | ||||||||||||
| 19 K |
20 Ca |
21 Sc |
22 Ti |
23 V |
24 Cr |
25 Mn |
26 Fe |
27 Co |
28 Ni |
29 Cu |
30 Zn |
31 Ga |
32 Ge |
33 As |
34 Se |
35 Br |
36 Kr | ||
| 37 Rb |
38 Sr |
39 Y |
40 Zr |
41 Nb |
42 Mo |
43 Tc |
44 Ru |
45 Rh |
46 Pd |
47 Ag |
48 Cd |
49 In |
50 Sn |
51 Sb |
52 Te |
53 I |
54 Xe | ||
| 55 Cs |
56 Ba |
71 Lu |
72 Hf |
73 Ta |
74 W |
75 Re |
76 Os |
77 Ir |
78 Pt |
79 Au |
80 Hg |
81 Tl |
82 Pb |
83 Bi |
84 Po |
85 At |
86 Rn | ||
| 87 Fr |
88 Ra |
103 Lr |
104 Rf |
105 Db |
106 Sg |
107 Bh |
108 Hs |
109 Mt |
110 Ds |
111 Rg |
112 Cn |
113 Nh |
114 Fl |
115 Mc |
116 Lv |
117 Ts |
118 Og | ||
| 57 La |
58 Ce |
59 Pr |
60 Nd |
61 Pm |
62 Sm |
63 Eu |
64 Gd |
65 Tb |
66 Dy |
67 Ho |
68 Er |
69 Tm |
70 Yb | ||||||
| 89 Ac |
90 Th |
91 Pa |
92 U |
93 Np |
94 Pu |
95 Am |
96 Cm |
97 Bk |
98 Cf |
99 Es |
100 Fm |
101 Md |
102 No | ||||||
| Legend: |
|---|
| predicted structure |
| Elements with known structure. |
| Body-centered cubic structure: W |
| Face-centered cubic structures: Cu |
| Primitive Hexagonal structures: Mg |
| unknown or uncertain |
Structure types
The following is a list of structure types which appear in the tables above. Regarding the number of atoms in the unit cell, structures in the rhombohedral lattice system have a rhombohedral primitive cell and have trigonal point symmetry but are also often also described in terms of an equivalent but nonprimitive hexagonal unit cell with three times the volume and three times the number of atoms.
| Prototype | Strukturbericht | Diagram | Lattice system | Space group | Atoms per unit cell | Coordination | notes |
|---|---|---|---|---|---|---|---|
| α-Pu | (none) |  |
Monoclinic | P21/m (No. 11) |
16 | slightly distorted hexagonal structure. Lattice parameters: a = 618.3 pm, b = 482.2 pm, c = 1096.3 pm, β = 101.79° | |
| β-S | (none) | Monoclinic | P21/c (No. 14) |
32 | |||
| α-Np | Ac | Orthorhombic | Pnma (No. 62) |
8 | highly distorted bcc structure. Lattice parameters: a = 666.3 pm, b = 472.3 pm, c = 488.7 pm | ||
| α-U | A20 |  |
Orthorhombic | Cmcm (No. 63) |
4 | Each atom has four near neighbours, 2 at 275.4 pm, 2 at 285.4 pm. The next four at distances 326.3 pm and four more at 334.2 pm. | Strongly distorted hcp structure. |
| α-Ga | A11 |  |
Orthorhombic | Cmce (No. 64) |
8 | each Ga atom has one nearest neighbour at 244 pm, 2 at 270 pm, 2 at 273 pm, 2 at 279 pm. | The structure is related to that of iodine. |
| b-P | A17 |  |
Orthorhombic | Cmce (No. 64) |
8 | Specifically the black phosphorus form of phosphorus. | |
| Cl | A14 |  |
Orthorhombic | Cmce (No. 64) |
8 | ||
| α-S | A16 | Orthorhombic | Fddd (No. 70) |
16 | |||
| In | A6 | 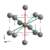 |
Tetragonal | I4/mmm (No. 139) |
2 | Identical symmetry to the α-Pa type structure. Can be considered slightly distorted from an ideal Cu type face-centered cubic structure which has . | |
| α-Pa | Aa | Tetragonal | I4/mmm (No. 139) |
2 | Identical symmetry to the In type structure. Can be considered slightly distorted from an ideal W type body centered cubic structure which has . | ||
| β-Sn | A5 | Tetragonal | I41/amd (No. 141) |
4 | 4 neighbours at 302 pm; 2 at 318 pm; 4 at 377 pm; 8 at 441 pm | white tin form (thermodynamical stable above 286.4 K) | |
| β-B | (none) |  |
Rhombohedral | R3m (No. 166) |
105 (rh.) 315 (hex.) |
Partly due to its complexity, whether this structure is the ground state of Boron has not been fully settled. | |
| α-As | A7 | Rhombohedral | R3m (No. 166) |
2 (rh.) 6 (hex.) |
in grey metallic form, each As atom has 3 neighbours in the same sheet at 251.7pm; 3 in adjacent sheet at 312.0 pm. each Bi atom has 3 neighbours in the same sheet at 307.2 pm; 3 in adjacent sheet at 352.9 pm. each Sb atom has 3 neighbours in the same sheet at 290.8pm; 3 in adjacent sheet at 335.5 pm. |
puckered sheet | |
| α-Sm | (none) |  |
Rhombohedral | R3m (No. 166) |
3 (rh.) 9 (hex.) |
12 nearest neighbours | complex hcp with 9-layer repeat: ABCBCACAB.... |
| α-Hg | A10 |  |
Rhombohedral | R3m (No. 166) |
1 (rh.) 3 (hex.) |
6 nearest neighbours at 234 K and 1 atm (it is liquid at room temperature and thus has no crystal structure at ambient conditions!) | Identical symmetry to the β-Po structure, distinguished based on details about the basis vectors of its unit cell. This structure can also be considered to be a distorted hcp lattice with the nearest neighbours in the same plane being approx 16% farther away |
| β-Po | Ai | Rhombohedral | R3m (No. 166) |
1 (rh.) 3 (hex.) |
Identical symmetry to the α-Hg structure, distinguished based on details about the basis vectors of its unit cell. | ||
| γ-Se | A8 | Hexagonal | P321 (No. 154) |
3 | |||
| Mg | A3 | Hexagonal | P63/mmc (No. 194) |
2 | Zn has 6 nearest neighbors in same plane: 6 in adjacent planes 14% farther away Cd has 6 nearest neighbours in the same plane- 6 in adjacent planes 15% farther away |
If the unit cell axial ratio is exactly the structure would be a mathematical hexagonal close packed (HCP) structure. However, in real materials there are deviations from this in some metals where the unit cell is distorted in one direction but the structure still retains the hcp space group—remarkable all the elements have a ratio of lattice parameters c/a < 1.633 (best are Mg and Co and worst Be with c/a ~ 1.568). In others like Zn and Cd the deviations from the ideal change the symmetry of the structure and these have a lattice parameter ratio c/a > 1.85. | |
| g-C | A9 |  |
Hexagonal | P63/mmc (No. 194) |
4 | Specifically the graphite form of carbon. | |
| α-La | A3' | Hexagonal | P63/mmc (No. 194) |
4 | The Double hexagonal close packed (DHCP) structure. Similar to the ideal hcp structure, the perfect dhcp structure should have a lattice parameter ratio of In the real dhcp structures of 5 lanthanides (including β-Ce) variates between 1.596 (Pm) and 1.6128 (Nd). For the four known actinides dhcp lattices the corresponding number vary between 1.620 (Bk) and 1.625 (Cf). | ||
| β-N | (none) | Hexagonal | P63/mmc (No. 194) |
4 | |||
| α-Po | Ah |  |
Cubic | Pm3m (No. 221) |
1 | 6 nearest neighbours | simple cubic lattice. The atoms in the unit cell are at the corner of a cube. |
| γ-O | (none) |  |
Cubic | Pm3n (No. 223) |
16 | Closely related to the β-W structure, except with a diatomic oxygen molecule in place of each tungsten atom. The molecules can rotate in place, but the direction of rotation for some of the molecules is restricted. | |
| α-Mn | A12 | Cubic | I43m (No. 217) |
58 | Unit cell contains Mn atoms in 4 different environments. | Distorted bcc | |
| W | A2 |  |
Cubic | Im3m (No. 229) |
2 | The Body centered cubic structure (BCC). It is not a close packed structure. In this each metal atom is at the centre of a cube with 8 nearest neighbors, however the 6 atoms at the centres of the adjacent cubes are only approximately 15% further away so the coordination number can therefore be considered to be 14 when these are on one 4 fold axe structure becomes face-centred cubic (cubic close packed). | |
| Cu | A1 |  |
Cubic | Fm3m (No. 225) |
4 | The face-centered cubic (cubic close packed) structure. More content relating to number of planes within structure and implications for glide/slide e.g. ductility. | |
| d-C | A4 | Cubic | Fd3m (No. 227) |
8 | The diamond cubic (DC) structure. Specifically the diamond form of Carbon. |
Close packed metal structures
See also: Close-packing of equal spheresThe observed crystal structures of many metals can be described as a nearly mathematical close-packing of equal spheres. A simple model for both of these is to assume that the metal atoms are spherical and are packed together as closely as possible. In closest packing, every atom has 12 equidistant nearest neighbours, and therefore a coordination number of 12. If the close packed structures are considered as being built of layers of spheres, then the difference between hexagonal close packing and face-centred cubic is how each layer is positioned relative to others. The following types can be viewed as a regular buildup of close-packed layers:
- Mg type (hexagonal close packing) has alternate layers positioned directly above/below each other: A,B,A,B,...
- Cu type (face-centered cubic) has every third layer directly above/below each other: A,B,C,A,B,C,...
- α-La type (double hexagonal close packing) has layers directly above/below each other, A,B,A,C,A,B,A,C,.... of period length 4 like an alternative mixture of fcc and hcp packing.
- α-Sm type has a period of 9 layers A,B,A,B,C,B,C,A,C,...
Precisely speaking, the structures of many of the elements in the groups above are slightly distorted from the ideal closest packing. While they retain the lattice symmetry as the ideal structure, they often have nonideal c/a ratios for their unit cell. Less precisely speaking, there are also other elements are nearly close-packed but have distortions which have at least one broken symmetry with respect to the close-packed structure:
- In type is slightly distorted from a cubic close packed structure
- α-Pa type is distorted from a hexagonal close packed structure
See also
References
- King, H.W. (2006-06-26). Lide, David R. (ed.). CRC Handbook of Chemistry and Physics (87 ed.). Boca Raton, Fla.: CRC Press. p. 12-15 to 12-18. ISBN 978-0-8493-0487-3.
- R. W. Gray; W. Ramsay (1909). "Some Physical Properties of Radium Emanation". J. Chem. Soc. Trans. 1909: 1073–1085. doi:10.1039/CT9099501073.
- Koufos, Alexander P.; Papaconstantopoulos, Dimitrios A. (2013). "Electronic Structure of Francium". International Journal of Quantum Chemistry. 113 (17): 2070–2077. doi:10.1002/qua.24466.
- ^ Arblaster, John W. (2018). Selected Values of the Crystallographic Properties of Elements. ASM International. p. 608. ISBN 978-1-62708-154-2.
- Florez, Edison; Smits, Odile R.; Mewes, Jan-Michael; Jerabek, Paul; Schwerdtfeger, Peter (2022). "From the gas phase to the solid state: The chemical bonding in the superheavy element flerovium". The Journal of Chemical Physics. 157. doi:10.1063/5.0097642.
- Hermann, A.; Hoffmann, R.; Ashcroft, N. W. (2013). "Condensed Astatine: Monatomic and Metallic". Physical Review Letters. 111 (11): 116404-1–116404-5. Bibcode:2013PhRvL.111k6404H. doi:10.1103/PhysRevLett.111.116404. PMID 24074111.
- ^ Grosse, A. V. (1965). "Some physical and chemical properties of element 118 (Eka-Em) and element 86 (Em)". Journal of Inorganic and Nuclear Chemistry. 27 (3). Elsevier Science Ltd.: 509–19. doi:10.1016/0022-1902(65)80255-X.
- ^ Östlin, A.; Vitos, L. (2011). "First-principles calculation of the structural stability of 6d transition metals". Physical Review B. 84 (11): 113104. Bibcode:2011PhRvB..84k3104O. doi:10.1103/PhysRevB.84.113104.
- Östlin, A. (2013). "Transition metals". Electronic Structure Studies and Method Development for Complex Materials (PDF) (Licentiate). pp. 15–16. Retrieved 24 October 2019.
- Mewes, J.-M.; Smits, O. R.; Kresse, G.; Schwerdtfeger, P. (2019). "Copernicium is a Relativistic Noble Liquid". Angewandte Chemie International Edition. doi:10.1002/anie.201906966. PMC 6916354.
- Atarah, Samuel A.; Egblewogbe, Martin N. H.; Hagoss, Gebreyesus G. (2020). "First principle study of the structural and electronic properties of Nihonium". MRS Advances: 1–9. doi:10.1557/adv.2020.159.
- ^ Fournier, Jean-Marc (1976). "Bonding and the electronic structure of the actinide metals". Journal of Physics and Chemistry of Solids. 37 (2): 235–244. Bibcode:1976JPCS...37..235F. doi:10.1016/0022-3697(76)90167-0.
- Lemire, R. J. et al.,2001
- URL "The alpha-Pu Structure". Archived from the original on 2011-12-30. Retrieved 2012-02-05.
- Lemire, R.J. et al.,Chemical Thermodynamics of Neptunium and Plutonium, Elsevier, Amsterdam, 2001
- URL "The alpha Np (A_c) Structure". Archived from the original on 2012-10-02. Retrieved 2013-10-16.
- Harry L. Yakel, A REVIEW OF X-RAY DIFFRACTION STUDIES IN URANIUM ALLOYS. The Physical Metallurgy of Uranium Alloys Conference, Vail, Colorado, Feb. 1974
- ^ Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Butterworth-Heinemann. ISBN 978-0-08-037941-8.
- A.F Wells (1962) Structural Inorganic Chemistry 3d Edition Oxford University Press
- Nevill Gonalez Swacki & Teresa Swacka, Basic elements of Crystallography, Pan Standford Publishing Pte. Ltd., 2010
- URL "The alpha la (A3') Structure". Archived from the original on 2011-12-23. Retrieved 2012-02-05.
- URL "The alpha Sm (C19) Structure". Archived from the original on 2012-01-12. Retrieved 2012-02-05.
- General
- P.A. Sterne; A. Gonis; A.A. Borovoi, eds. (July 1996). "Actinides and the Environment". Proc. of the NATO Advanced Study Institute on Actinides and the Environment. NATO ASI Series. Maleme, Crete, Greece: Kluver Academic Publishers. pp. 59–61. ISBN 0-7923-4968-7.
- L.R. Morss; Norman M. Edelstein; Jean Fuger, eds. (2007). The Chemistry of the Actinide and Transactinide Elements (3rd ed.). Springer. ISBN 978-1402035555.
External links
- Strukturbericht Type A – structure reports for the pure elements
- Crystal Structures for the solid chemical elements at 1 bar
| Periodic table | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Periodic table forms | |||||||||||||||||||
| Sets of elements |
| ||||||||||||||||||
| Elements | |||||||||||||||||||
| History | |||||||||||||||||||
| See also | |||||||||||||||||||
 .
.
 .
.
 the structure would be a mathematical
the structure would be a mathematical  In the real dhcp structures of 5 lanthanides (including β-Ce)
In the real dhcp structures of 5 lanthanides (including β-Ce)  variates between 1.596 (Pm) and 1.6128 (Nd). For the four known actinides dhcp lattices the corresponding number vary between 1.620 (Bk) and 1.625 (Cf).
variates between 1.596 (Pm) and 1.6128 (Nd). For the four known actinides dhcp lattices the corresponding number vary between 1.620 (Bk) and 1.625 (Cf).