Misplaced Pages

Ducci sequence

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Sequence of n-tuples of integers

A Ducci sequence is a sequence of n-tuples of integers, sometimes known as "the Diffy game", because it is based on sequences.

Given an n-tuple of integers ( a 1 , a 2 , . . . , a n ) {\displaystyle (a_{1},a_{2},...,a_{n})} , the next n-tuple in the sequence is formed by taking the absolute differences of neighbouring integers:

( a 1 , a 2 , . . . , a n ) → ( | a 1 − a 2 | , | a 2 − a 3 | , . . . , | a n − a 1 | ) . {\displaystyle (a_{1},a_{2},...,a_{n})\rightarrow (|a_{1}-a_{2}|,|a_{2}-a_{3}|,...,|a_{n}-a_{1}|)\,.}

Another way of describing this is as follows. Arrange n integers in a circle and make a new circle by taking the difference between neighbours, ignoring any minus signs; then repeat the operation. Ducci sequences are named after Enrico Ducci (1864–1940), the Italian mathematician who discovered in the 1930s that every such sequence eventually becomes periodic.

Ducci sequences are also known as the Ducci map or the n-number game. Open problems in the study of these maps still remain.

Properties

From the second n-tuple onwards, it is clear that every integer in each n-tuple in a Ducci sequence is greater than or equal to 0 and is less than or equal to the difference between the maximum and minimum members of the first n-tuple. As there are only a finite number of possible n-tuples with these constraints, the sequence of n-tuples must sooner or later repeat itself. Every Ducci sequence therefore eventually becomes periodic.

If n is a power of 2 every Ducci sequence eventually reaches the n-tuple (0,0,...,0) in a finite number of steps.

If n is not a power of two, a Ducci sequence will either eventually reach an n-tuple of zeros or will settle into a periodic loop of 'binary' n-tuples; that is, n-tuples of form k ( b 1 , b 2 , . . . b n ) {\displaystyle k(b_{1},b_{2},...b_{n})} , k {\displaystyle k} is a constant, and b i ∈ { 0 , 1 } {\displaystyle b_{i}\in \{0,1\}} .

An obvious generalisation of Ducci sequences is to allow the members of the n-tuples to be any real numbers rather than just integers. For example, this 4-tuple converges to (0, 0, 0, 0) in four iterations: ( e , π , 2 , 1 ) → ( π − e , π − 2 , 2 − 1 , e − 1 ) → ( e − 2 , π − 2 2 + 1 , e − 2 , 2 e − π − 1 ) → {\displaystyle (e,\pi ,{\sqrt {2}},1)\rightarrow (\pi -e,\pi -{\sqrt {2}},{\sqrt {2}}-1,e-1)\rightarrow (e-{\sqrt {2}},\pi -2{\sqrt {2}}+1,e-{\sqrt {2}},2e-\pi -1)\rightarrow } ( π − e − 2 + 1 , π − e − 2 + 1 , π − e − 2 + 1 , π − e − 2 + 1 ) → ( 0 , 0 , 0 , 0 ) {\displaystyle (\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1,\pi -e-{\sqrt {2}}+1)\rightarrow (0,0,0,0)}

The properties presented here do not always hold for these generalisations. For example, a Ducci sequence starting with the n-tuple (1, q, q, q) where q is the (irrational) positive root of the cubic x 3 − x 2 − x − 1 = 0 {\displaystyle x^{3}-x^{2}-x-1=0} does not reach (0,0,0,0) in a finite number of steps, although in the limit it converges to (0,0,0,0).

Examples

Ducci sequences may be arbitrarily long before they reach a tuple of zeros or a periodic loop. The 4-tuple sequence starting with (0, 653, 1854, 4063) takes 24 iterations to reach the zeros tuple.

( 0 , 653 , 1854 , 4063 ) → ( 653 , 1201 , 2209 , 4063 ) → ( 548 , 1008 , 1854 , 3410 ) → {\displaystyle (0,653,1854,4063)\rightarrow (653,1201,2209,4063)\rightarrow (548,1008,1854,3410)\rightarrow } ⋯ → ( 0 , 0 , 128 , 128 ) → ( 0 , 128 , 0 , 128 ) → ( 128 , 128 , 128 , 128 ) → ( 0 , 0 , 0 , 0 ) {\displaystyle \cdots \rightarrow (0,0,128,128)\rightarrow (0,128,0,128)\rightarrow (128,128,128,128)\rightarrow (0,0,0,0)}

This 5-tuple sequence enters a period 15 binary 'loop' after 7 iterations.

15799 → 42208 → 20284 → 22642 → 04220 → 42020 → 22224 → 00022 → 00202 → 02222 → 20002 → 20020 → 20222 → 22000 → 02002 → 22022 → 02200 → 20200 → 22202 → 00220 → 02020 → 22220 → 00022 → ⋯ {\displaystyle {\begin{matrix}15799\rightarrow &42208\rightarrow &20284\rightarrow &22642\rightarrow &04220\rightarrow &42020\rightarrow \\22224\rightarrow &00022\rightarrow &00202\rightarrow &02222\rightarrow &20002\rightarrow &20020\rightarrow \\20222\rightarrow &22000\rightarrow &02002\rightarrow &22022\rightarrow &02200\rightarrow &20200\rightarrow \\22202\rightarrow &00220\rightarrow &02020\rightarrow &22220\rightarrow &00022\rightarrow &\cdots \quad \quad \\\end{matrix}}}

The following 6-tuple sequence shows that sequences of tuples whose length is not a power of two may still reach a tuple of zeros:

121210 → 111111 → 000000 {\displaystyle {\begin{matrix}121210\rightarrow &111111\rightarrow &000000\\\end{matrix}}}

If some conditions are imposed on any "power of two"-tuple Ducci sequence, it would take that power of two or lesser iterations to reach the zeros tuple. It is hypothesized that these sequences conform to a rule.

Modulo two form

When the Ducci sequences enter binary loops, it is possible to treat the sequence in modulo two. That is:

( | a 1 − a 2 | , | a 2 − a 3 | , . . . , | a n − a 1 | )   = ( a 1 + a 2 , a 2 + a 3 , . . . , a n + a 1 ) mod 2 {\displaystyle (|a_{1}-a_{2}|,|a_{2}-a_{3}|,...,|a_{n}-a_{1}|)\ =(a_{1}+a_{2},a_{2}+a_{3},...,a_{n}+a_{1}){\bmod {2}}}

This forms the basis for proving when the sequence vanish to all zeros.

Cellular automata

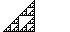
The linear map in modulo 2 can further be identified as the cellular automata denoted as rule 102 in Wolfram code and related to rule 90 through the Martin-Odlyzko-Wolfram map. Rule 102 reproduces the Sierpinski triangle.

Other related topics

The Ducci map is an example of a difference equation, a category that also include non-linear dynamics, chaos theory and numerical analysis. Similarities to cyclotomic polynomials have also been pointed out. While there are no practical applications of the Ducci map at present, its connection to the highly applied field of difference equations led to conjecture that a form of the Ducci map may also find application in the future.

References

  1. ^ Chamberland, Marc; Thomas, Diana M. (2004). "The N-Number Ducci Game" (PDF). Journal of Difference Equations and Applications. 10 (3): 33–36. doi:10.1080/10236190410001647807. Retrieved 2009-01-26.
  2. ^ Clausing, Achim (2018). "Ducci matrices". American Mathematical Monthly. 125 (10): 901–921. doi:10.1080/00029890.2018.1523661.
  3. Chamberland, Marc (2003). "Unbounded Ducci sequences" (PDF). Journal of Difference Equations and Applications. 9 (10): 887–895. CiteSeerX 10.1.1.63.6652. doi:10.1080/1023619021000041424. Retrieved 2009-01-26.
  4. Andriychenko, Oleksiy; Chamberland, Marc (2000). "Iterated Strings and Cellular Automata". The Mathematical Intelligencer. 22 (4): 33–36. doi:10.1007/BF03026764.
  5. ^ Brockman, Greg (2007). "Asymptotic behaviour of certain Ducci sequences" (PDF). Fibonacci Quarterly.
  6. Euich, Miztani; Akihiro, Nozaki.; Toru, Sawatari. (2013). "A Conjecture of Ducci Sequences and the Aspects" (PDF). RIMS Kokyuroku. 1873: 88–97. Retrieved 2014-02-18.
  7. Florian Breuer, "Ducci sequences in higher dimensions" in INTEGERS: ELECTRONIC JOURNAL OF COMBINATORIAL NUMBER THEORY 7 (2007)
  8. S Lettieri, JG Stevens, DM Thomas, "Characteristic and minimal polynomials of linear cellular automata" in Rocky Mountain J. Math, 2006.
  9. M Misiurewicz, JG Stevens, DM Thomas, "Iterations of linear maps over finite fields", Linear Algebra and Its Applications, 2006
  10. Weisstein, Eric W. "Rule 102." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Rule102.html
  11. F. Breuer et al. 'Ducci-sequences and cyclotomic polynomials' in Finite Fields and Their Applications 13 (2007) 293–304

External links

Categories: