| Differential equations | ||||||
|---|---|---|---|---|---|---|
| Scope | ||||||
Fields
List of named differential equations |
||||||
| Classification | ||||||
Types
|
||||||
| Relation to processes | ||||||
| Solution | ||||||
| Existence and uniqueness | ||||||
| General topics | ||||||
| Solution methods | ||||||
| People | ||||||
| List | ||||||
In mathematics and computational science, the Euler method (also called the forward Euler method) is a first-order numerical procedure for solving ordinary differential equations (ODEs) with a given initial value. It is the most basic explicit method for numerical integration of ordinary differential equations and is the simplest Runge–Kutta method. The Euler method is named after Leonhard Euler, who first proposed it in his book Institutionum calculi integralis (published 1768–1770).
The Euler method is a first-order method, which means that the local error (error per step) is proportional to the square of the step size, and the global error (error at a given time) is proportional to the step size. The Euler method often serves as the basis to construct more complex methods, e.g., predictor–corrector method.
Geometrical description
Purpose and why it works
Consider the problem of calculating the shape of an unknown curve which starts at a given point and satisfies a given differential equation. Here, a differential equation can be thought of as a formula by which the slope of the tangent line to the curve can be computed at any point on the curve, once the position of that point has been calculated.
The idea is that while the curve is initially unknown, its starting point, which we denote by is known (see Figure 1). Then, from the differential equation, the slope to the curve at can be computed, and so, the tangent line.
Take a small step along that tangent line up to a point Along this small step, the slope does not change too much, so will be close to the curve. If we pretend that is still on the curve, the same reasoning as for the point above can be used. After several steps, a polygonal curve () is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite.
First-order process
When given the values for and , and the derivative of is a given function of and denoted as . Begin the process by setting . Next, choose a value for the size of every step along t-axis, and set (or equivalently ). Now, the Euler method is used to find from and :
The value of is an approximation of the solution at time , i.e., . The Euler method is explicit, i.e. the solution is an explicit function of for .
Higher-order process
While the Euler method integrates a first-order ODE, any ODE of order can be represented as a system of first-order ODEs. When given the ODE of order defined as
as well as , , and , we implement the following formula until we reach the approximation of the solution to the ODE at the desired time:
These first-order systems can be handled by Euler's method or, in fact, by any other scheme for first-order systems.
First-order example
Given the initial value problem
we would like to use the Euler method to approximate .
Using step size equal to 1 (h = 1)

The Euler method is
so first we must compute . In this simple differential equation, the function is defined by . We have
By doing the above step, we have found the slope of the line that is tangent to the solution curve at the point . Recall that the slope is defined as the change in divided by the change in , or .
The next step is to multiply the above value by the step size , which we take equal to one here:
Since the step size is the change in , when we multiply the step size and the slope of the tangent, we get a change in value. This value is then added to the initial value to obtain the next value to be used for computations.
The above steps should be repeated to find , and .
Due to the repetitive nature of this algorithm, it can be helpful to organize computations in a chart form, as seen below, to avoid making errors.
0 1 0 1 1 1 2 1 2 1 2 1 2 4 2 4 2 4 1 4 8 3 8 3 8 1 8 16
The conclusion of this computation is that . The exact solution of the differential equation is , so . Although the approximation of the Euler method was not very precise in this specific case, particularly due to a large value step size , its behaviour is qualitatively correct as the figure shows.
Using other step sizes
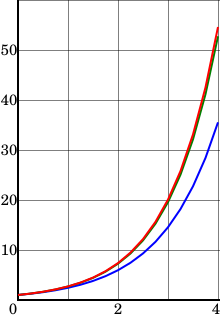
As suggested in the introduction, the Euler method is more accurate if the step size is smaller. The table below shows the result with different step sizes. The top row corresponds to the example in the previous section, and the second row is illustrated in the figure.
step size result of Euler's method error 1 16.00 38.60 0.25 35.53 19.07 0.1 45.26 09.34 0.05 49.56 05.04 0.025 51.98 02.62 0.0125 53.26 01.34
The error recorded in the last column of the table is the difference between the exact solution at and the Euler approximation. In the bottom of the table, the step size is half the step size in the previous row, and the error is also approximately half the error in the previous row. This suggests that the error is roughly proportional to the step size, at least for fairly small values of the step size. This is true in general, also for other equations; see the section Global truncation error for more details.
Other methods, such as the midpoint method also illustrated in the figures, behave more favourably: the global error of the midpoint method is roughly proportional to the square of the step size. For this reason, the Euler method is said to be a first-order method, while the midpoint method is second order.
We can extrapolate from the above table that the step size needed to get an answer that is correct to three decimal places is approximately 0.00001, meaning that we need 400,000 steps. This large number of steps entails a high computational cost. For this reason, higher-order methods are employed such as Runge–Kutta methods or linear multistep methods, especially if a high accuracy is desired.
Higher-order example
For this third-order example, assume that the following information is given:
From this we can isolate y''' to get the equation:
Using that we can get the solution for :And using the solution for , we can get the solution for :We can continue this process using the same formula as long as necessary to find whichever desired.
Derivation
The Euler method can be derived in a number of ways.
(1) Firstly, there is the geometrical description above.
(2) Another possibility is to consider the Taylor expansion of the function around :
The differential equation states that . If this is substituted in the Taylor expansion and the quadratic and higher-order terms are ignored, the Euler method arises.
The Taylor expansion is used below to analyze the error committed by the Euler method, and it can be extended to produce Runge–Kutta methods.
(3) A closely related derivation is to substitute the forward finite difference formula for the derivative,
in the differential equation . Again, this yields the Euler method.
A similar computation leads to the midpoint method and the backward Euler method.
(4) Finally, one can integrate the differential equation from to and apply the fundamental theorem of calculus to get:
Now approximate the integral by the left-hand rectangle method (with only one rectangle):
Combining both equations, one finds again the Euler method.
This line of thought can be continued to arrive at various linear multistep methods.
Local truncation error
The local truncation error of the Euler method is the error made in a single step. It is the difference between the numerical solution after one step, , and the exact solution at time . The numerical solution is given by
For the exact solution, we use the Taylor expansion mentioned in the section Derivation above:
The local truncation error (LTE) introduced by the Euler method is given by the difference between these equations:
This result is valid if has a bounded third derivative.
This shows that for small , the local truncation error is approximately proportional to . This makes the Euler method less accurate than higher-order techniques such as Runge-Kutta methods and linear multistep methods, for which the local truncation error is proportional to a higher power of the step size.
A slightly different formulation for the local truncation error can be obtained by using the Lagrange form for the remainder term in Taylor's theorem. If has a continuous second derivative, then there exists a such that
In the above expressions for the error, the second derivative of the unknown exact solution can be replaced by an expression involving the right-hand side of the differential equation. Indeed, it follows from the equation that
Global truncation error
The global truncation error is the error at a fixed time , after however many steps the method needs to take to reach that time from the initial time. The global truncation error is the cumulative effect of the local truncation errors committed in each step. The number of steps is easily determined to be , which is proportional to , and the error committed in each step is proportional to (see the previous section). Thus, it is to be expected that the global truncation error will be proportional to .
This intuitive reasoning can be made precise. If the solution has a bounded second derivative and is Lipschitz continuous in its second argument, then the global truncation error (denoted as ) is bounded by
where is an upper bound on the second derivative of on the given interval and is the Lipschitz constant of . Or more simply, when , the value (such that is treated as a constant). In contrast, where function is the exact solution which only contains the variable.
The precise form of this bound is of little practical importance, as in most cases the bound vastly overestimates the actual error committed by the Euler method. What is important is that it shows that the global truncation error is (approximately) proportional to . For this reason, the Euler method is said to be first order.
Example
If we have the differential equation , and the exact solution , and we want to find and for when . Thus we can find the error bound at t=2.5 and h=0.5:
Notice that t0 is equal to 2 because it is the lower bound for t in .
Numerical stability

The Euler method can also be numerically unstable, especially for stiff equations, meaning that the numerical solution grows very large for equations where the exact solution does not. This can be illustrated using the linear equation
The exact solution is , which decays to zero as . However, if the Euler method is applied to this equation with step size , then the numerical solution is qualitatively wrong: It oscillates and grows (see the figure). This is what it means to be unstable. If a smaller step size is used, for instance , then the numerical solution does decay to zero.

If the Euler method is applied to the linear equation , then the numerical solution is unstable if the product is outside the region
illustrated on the right. This region is called the (linear) stability region. In the example, , so if then which is outside the stability region, and thus the numerical solution is unstable.
This limitation — along with its slow convergence of error with — means that the Euler method is not often used, except as a simple example of numerical integration. Frequently models of physical systems contain terms representing fast-decaying elements (i.e. with large negative exponential arguments). Even when these are not of interest in the overall solution, the instability they can induce means that an exceptionally small timestep would be required if the Euler method is used.
Rounding errors
In step of the Euler method, the rounding error is roughly of the magnitude where is the machine epsilon. Assuming that the rounding errors are independent random variables, the expected total rounding error is proportional to . Thus, for extremely small values of the step size the truncation error will be small but the effect of rounding error may be big. Most of the effect of rounding error can be easily avoided if compensated summation is used in the formula for the Euler method.
Modifications and extensions
A simple modification of the Euler method which eliminates the stability problems noted above is the backward Euler method:
This differs from the (standard, or forward) Euler method in that the function is evaluated at the end point of the step, instead of the starting point. The backward Euler method is an implicit method, meaning that the formula for the backward Euler method has on both sides, so when applying the backward Euler method we have to solve an equation. This makes the implementation more costly.
Other modifications of the Euler method that help with stability yield the exponential Euler method or the semi-implicit Euler method.
More complicated methods can achieve a higher order (and more accuracy). One possibility is to use more function evaluations. This is illustrated by the midpoint method which is already mentioned in this article:
- .
This leads to the family of Runge–Kutta methods.
The other possibility is to use more past values, as illustrated by the two-step Adams–Bashforth method:
This leads to the family of linear multistep methods. There are other modifications which uses techniques from compressive sensing to minimize memory usage
In popular culture
In the film Hidden Figures, Katherine Goble resorts to the Euler method in calculating the re-entry of astronaut John Glenn from Earth orbit.
See also
- Crank–Nicolson method
- Gradient descent similarly uses finite steps, here to find minima of functions
- List of Runge-Kutta methods
- Linear multistep method
- Numerical integration (for calculating definite integrals)
- Numerical methods for ordinary differential equations
Notes
- Butcher 2003, p. 45; Hairer, Nørsett & Wanner 1993, p. 35
- Atkinson 1989, p. 342; Butcher 2003, p. 60
- Butcher 2003, p. 45; Hairer, Nørsett & Wanner 1993, p. 36
- Butcher 2003, p. 3; Hairer, Nørsett & Wanner 1993, p. 2
- See also Atkinson 1989, p. 344
- Hairer, Nørsett & Wanner 1993, p. 40
- Atkinson 1989, p. 342; Hairer, Nørsett & Wanner 1993, p. 36
- Atkinson 1989, p. 342
- Atkinson 1989, p. 343
- Butcher 2003, p. 60
- Atkinson 1989, p. 342
- Stoer & Bulirsch 2002, p. 474
- Atkinson 1989, p. 344
- Butcher 2003, p. 49
- Atkinson 1989, p. 346; Lakoba 2012, equation (1.16)
- Iserles 1996, p. 7
- Butcher 2003, p. 63
- Butcher 2003, p. 70; Iserles 1996, p. 57
- Butcher 2003, pp. 74–75
- Butcher 2003, pp. 75–78
- Unni, M. P.; Chandra, M. G.; Kumar, A. A. (March 2017). "Memory reduction for numerical solution of differential equations using compressive sensing". 2017 IEEE 13th International Colloquium on Signal Processing & its Applications (CSPA). pp. 79–84. doi:10.1109/CSPA.2017.8064928. ISBN 978-1-5090-1184-1. S2CID 13082456.
- Khan, Amina (9 January 2017). "Meet the 'Hidden Figures' mathematician who helped send Americans into space". Los Angeles Times. Retrieved 12 February 2017.
References
- Atkinson, Kendall A. (1989). An Introduction to Numerical Analysis (2nd ed.). New York: John Wiley & Sons. ISBN 978-0-471-50023-0.
- Ascher, Uri M.; Petzold, Linda R. (1998). Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations. Philadelphia: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-412-8.
- Butcher, John C. (2003). Numerical Methods for Ordinary Differential Equations. New York: John Wiley & Sons. ISBN 978-0-471-96758-3.
- Hairer, Ernst; Nørsett, Syvert Paul; Wanner, Gerhard (1993). Solving ordinary differential equations I: Nonstiff problems. Berlin, New York: Springer-Verlag. ISBN 978-3-540-56670-0.
- Iserles, Arieh (1996). A First Course in the Numerical Analysis of Differential Equations. Cambridge University Press. ISBN 978-0-521-55655-2.
- Stoer, Josef; Bulirsch, Roland (2002). Introduction to Numerical Analysis (3rd ed.). Berlin, New York: Springer-Verlag. ISBN 978-0-387-95452-3.
- Lakoba, Taras I. (2012), Simple Euler method and its modifications (PDF) (Lecture notes for MATH334), University of Vermont, retrieved 29 February 2012
- Unni, M P. (2017). "Memory reduction for numerical solution of differential equations using compressive sensing". 2017 IEEE 13th International Colloquium on Signal Processing & its Applications (CSPA). IEEE CSPA. pp. 79–84. doi:10.1109/CSPA.2017.8064928. ISBN 978-1-5090-1184-1. S2CID 13082456.
External links
 Media related to Euler method at Wikimedia Commons
Media related to Euler method at Wikimedia Commons- Euler method implementations in different languages by Rosetta Code
- "Euler method", Encyclopedia of Mathematics, EMS Press, 2001
| Numerical methods for ordinary differential equations | |
|---|---|
| First-order methods | |
| Second-order methods | |
| Higher-order methods | |
| Theory | |
 is known (see Figure 1). Then, from the differential equation, the slope to the curve at
is known (see Figure 1). Then, from the differential equation, the slope to the curve at  can be computed, and so, the tangent line.
can be computed, and so, the tangent line.
 Along this small step, the slope does not change too much, so
Along this small step, the slope does not change too much, so  will be close to the curve. If we pretend that
will be close to the curve. If we pretend that  ) is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite.
) is computed. In general, this curve does not diverge too far from the original unknown curve, and the error between the two curves can be made small if the step size is small enough and the interval of computation is finite.
 and
and  , and the derivative of
, and the derivative of  is a given function of
is a given function of  and
and  . Begin the process by setting
. Begin the process by setting  . Next, choose a value
. Next, choose a value  for the size of every step along t-axis, and set
for the size of every step along t-axis, and set  (or equivalently
(or equivalently  ). Now, the Euler method is used to find
). Now, the Euler method is used to find  from
from  and
and  :
:

 . The Euler method is
. The Euler method is  for
for  .
.
 can be represented as a system of first-order ODEs. When given the ODE of order
can be represented as a system of first-order ODEs. When given the ODE of order 
 , we implement the following formula until we reach the approximation of the solution to the ODE at the desired time:
, we implement the following formula until we reach the approximation of the solution to the ODE at the desired time:


 .
.
 Blue is the Euler method; green, the
Blue is the Euler method; green, the  The step size is
The step size is 
 . In this simple differential equation, the function
. In this simple differential equation, the function  is defined by
is defined by  . We have
. We have

 . Recall that the slope is defined as the change in
. Recall that the slope is defined as the change in  .
.


 ,
,  and
and  .
.




 . The exact solution of the differential equation is
. The exact solution of the differential equation is  , so
, so  . Although the approximation of the Euler method was not very precise in this specific case, particularly due to a large value step size
. Although the approximation of the Euler method was not very precise in this specific case, particularly due to a large value step size 
 and the Euler approximation. In the bottom of the table, the step size is half the step size in the previous row, and the error is also approximately half the error in the previous row. This suggests that the error is roughly proportional to the step size, at least for fairly small values of the step size. This is true in general, also for other equations; see the section
and the Euler approximation. In the bottom of the table, the step size is half the step size in the previous row, and the error is also approximately half the error in the previous row. This suggests that the error is roughly proportional to the step size, at least for fairly small values of the step size. This is true in general, also for other equations; see the section 

 :
: And using the solution for
And using the solution for  :
: We can continue this process using the same formula as long as necessary to find whichever
We can continue this process using the same formula as long as necessary to find whichever  desired.
desired.

 . If this is substituted in the Taylor expansion and the quadratic and higher-order terms are ignored, the Euler method arises.
. If this is substituted in the Taylor expansion and the quadratic and higher-order terms are ignored, the Euler method arises.

 and apply the
and apply the 

 , and the exact solution at time
, and the exact solution at time  . The numerical solution is given by
. The numerical solution is given by


 . This makes the Euler method less accurate than higher-order techniques such as
. This makes the Euler method less accurate than higher-order techniques such as  such that
such that


 , after however many steps the method needs to take to reach that time from the initial time. The global truncation error is the cumulative effect of the local truncation errors committed in each step. The number of steps is easily determined to be
, after however many steps the method needs to take to reach that time from the initial time. The global truncation error is the cumulative effect of the local truncation errors committed in each step. The number of steps is easily determined to be  , which is proportional to
, which is proportional to  , and the error committed in each step is proportional to
, and the error committed in each step is proportional to  ) is bounded by
) is bounded by

 is an upper bound on the second derivative of
is an upper bound on the second derivative of  is the Lipschitz constant of
is the Lipschitz constant of  , the value
, the value  (such that
(such that  where function
where function  is the exact solution which only contains the
is the exact solution which only contains the  , and the exact solution
, and the exact solution  , and we want to find
, and we want to find  .
. 
 Thus we can find the error bound at t=2.5 and h=0.5:
Thus we can find the error bound at t=2.5 and h=0.5:
 Notice that t0 is equal to 2 because it is the lower bound for t in
Notice that t0 is equal to 2 because it is the lower bound for t in  computed with the Euler method with step size
computed with the Euler method with step size  (blue squares) and
(blue squares) and  (red circles). The black curve shows the exact solution.
(red circles). The black curve shows the exact solution.
 , which decays to zero as
, which decays to zero as  . However, if the Euler method is applied to this equation with step size
. However, if the Euler method is applied to this equation with step size  , then the numerical solution is unstable if the product
, then the numerical solution is unstable if the product  is outside the region
is outside the region

 , so if
, so if  which is outside the stability region, and thus the numerical solution is unstable.
which is outside the stability region, and thus the numerical solution is unstable.
 where
where  is the
is the  . Thus, for extremely small values of the step size the truncation error will be small but the effect of rounding error may be big. Most of the effect of rounding error can be easily avoided if
. Thus, for extremely small values of the step size the truncation error will be small but the effect of rounding error may be big. Most of the effect of rounding error can be easily avoided if 
 .
.