Even and odd functions - Misplaced Pages

(Redirected from Even–odd decomposition) Functions such that f(–x) equals f(x) or –f(x) Not to be confused with Even and odd numbers.

In mathematics, an even function is a real function such that $f(-x)=f(x)$ for every $x$ in its domain. Similarly, an odd function is a function such that $f(-x)=-f(x)$ for every $x$ in its domain.

They are named for the parity of the powers of the power functions which satisfy each condition: the function $f(x)=x^{n}$ is even if n is an even integer, and it is odd if n is an odd integer.

Even functions are those real functions whose graph is self-symmetric with respect to the y-axis, and odd functions are those whose graph is self-symmetric with respect to the origin.

If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely decomposed as the sum of an even function and an odd function.

Definition and examples

Evenness and oddness are generally considered for real functions, that is real-valued functions of a real variable. However, the concepts may be more generally defined for functions whose domain and codomain both have a notion of additive inverse. This includes abelian groups, all rings, all fields, and all vector spaces. Thus, for example, a real function could be odd or even (or neither), as could a complex-valued function of a vector variable, and so on.

The given examples are real functions, to illustrate the symmetry of their graphs.

Even functions

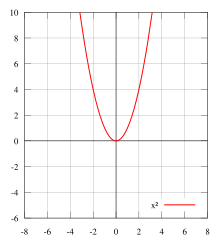
{\displaystyle f(x)=x^{2}} — $f(x)=x^{2}$ is an example of an even function.

A real function f is even if, for every x in its domain, −x is also in its domain and $f(-x)=f(x)$ or equivalently $f(x)-f(-x)=0.$

Geometrically, the graph of an even function is symmetric with respect to the y-axis, meaning that its graph remains unchanged after reflection about the y-axis.

Examples of even functions are:

The absolute value $x\mapsto |x|,$
$x\mapsto x^{2},$
$x\mapsto x^{4},$
cosine $\cos ,$
hyperbolic cosine $\cosh ,$
Gaussian function $x\mapsto \exp(-x^{2}).$

Odd functions

{\displaystyle f(x)=x^{3}} — $f(x)=x^{3}$ is an example of an odd function.

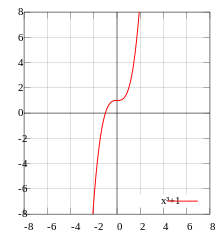
A real function f is odd if, for every x in its domain, −x is also in its domain and $f(-x)=-f(x)$ or equivalently $f(x)+f(-x)=0.$

Geometrically, the graph of an odd function has rotational symmetry with respect to the origin, meaning that its graph remains unchanged after rotation of 180 degrees about the origin.

If $x=0$ is in the domain of an odd function $f(x)$ , then $f(0)=0$ .

Examples of odd functions are:

The sign function $x\mapsto \operatorname {sgn}(x),$
The identity function $x\mapsto x,$
$x\mapsto x^{3},$
sine $\sin ,$
hyperbolic sine $\sinh ,$
The error function $\operatorname {erf} .$

{\displaystyle f(x)=x^{3}+1} — $f(x)=x^{3}+1$ is neither even nor odd.

Basic properties

Uniqueness

If a function is both even and odd, it is equal to 0 everywhere it is defined.
If a function is odd, the absolute value of that function is an even function.

Addition and subtraction

The sum of two even functions is even.
The sum of two odd functions is odd.
The difference between two odd functions is odd.
The difference between two even functions is even.
The sum of an even and odd function is not even or odd, unless one of the functions is equal to zero over the given domain.

Multiplication and division

The product of two even functions is an even function.
- That implies that product of any number of even functions is an even function as well.
The product of two odd functions is an even function.
The product of an even function and an odd function is an odd function.
The quotient of two even functions is an even function.
The quotient of two odd functions is an even function.
The quotient of an even function and an odd function is an odd function.

Composition

The composition of two even functions is even.
The composition of two odd functions is odd.
The composition of an even function and an odd function is even.
The composition of any function with an even function is even (but not vice versa).

Even–odd decomposition

If a real function has a domain that is self-symmetric with respect to the origin, it may be uniquely decomposed as the sum of an even and an odd function, which are called respectively the even part (or the even component) and the odd part (or the odd component) of the function, and are defined by $f_{\text{even}}(x)={\frac {f(x)+f(-x)}{2}},$ and $f_{\text{odd}}(x)={\frac {f(x)-f(-x)}{2}}.$

It is straightforward to verify that $f_{\text{even}}$ is even, $f_{\text{odd}}$ is odd, and $f=f_{\text{even}}+f_{\text{odd}}.$

This decomposition is unique since, if

f(x)=g(x)+h(x),

where g is even and h is odd, then $g=f_{\text{even}}$ and $h=f_{\text{odd}},$ since

{\begin{aligned}2f_{\text{e}}(x)&=f(x)+f(-x)=g(x)+g(-x)+h(x)+h(-x)=2g(x),\\2f_{\text{o}}(x)&=f(x)-f(-x)=g(x)-g(-x)+h(x)-h(-x)=2h(x).\end{aligned}}

For example, the hyperbolic cosine and the hyperbolic sine may be regarded as the even and odd parts of the exponential function, as the first one is an even function, the second one is odd, and

e^{x}=\underbrace {\cosh(x)} _{f_{\text{even}}(x)}+\underbrace {\sinh(x)} _{f_{\text{odd}}(x)}

Fourier's sine and cosine transforms also perform even–odd decomposition by representing a function's odd part with sine waves (an odd function) and the function's even part with cosine waves (an even function).

Further algebraic properties

Any linear combination of even functions is even, and the even functions form a vector space over the reals. Similarly, any linear combination of odd functions is odd, and the odd functions also form a vector space over the reals. In fact, the vector space of all real functions is the direct sum of the subspaces of even and odd functions. This is a more abstract way of expressing the property in the preceding section.
- The space of functions can be considered a graded algebra over the real numbers by this property, as well as some of those above.

The even functions form a commutative algebra over the reals. However, the odd functions do not form an algebra over the reals, as they are not closed under multiplication.

Analytic properties

A function's being odd or even does not imply differentiability, or even continuity. For example, the Dirichlet function is even, but is nowhere continuous.

In the following, properties involving derivatives, Fourier series, Taylor series are considered, and these concepts are thus supposed to be defined for the considered functions.

Basic analytic properties

The derivative of an even function is odd.
The derivative of an odd function is even.
The integral of an odd function from −A to +A is zero (where A is finite, and the function has no vertical asymptotes between −A and A). For an odd function that is integrable over a symmetric interval, e.g. $[- A, A]$ , the result of the integral over that interval is zero; that is
$\int _{-A}^{A}f(x)\,dx=0$ .
The integral of an even function from −A to +A is twice the integral from 0 to +A (where A is finite, and the function has no vertical asymptotes between −A and A. This also holds true when A is infinite, but only if the integral converges); that is
$\int _{-A}^{A}f(x)\,dx=2\int _{0}^{A}f(x)\,dx$ .

Series

The Maclaurin series of an even function includes only even powers.
The Maclaurin series of an odd function includes only odd powers.
The Fourier series of a periodic even function includes only cosine terms.
The Fourier series of a periodic odd function includes only sine terms.
The Fourier transform of a purely real-valued even function is real and even. (see Fourier analysis § Symmetry properties)
The Fourier transform of a purely real-valued odd function is imaginary and odd. (see Fourier analysis § Symmetry properties)

Harmonics

In signal processing, harmonic distortion occurs when a sine wave signal is sent through a memory-less nonlinear system, that is, a system whose output at time t only depends on the input at time t and does not depend on the input at any previous times. Such a system is described by a response function $V_{\text{out}}(t)=f(V_{\text{in}}(t))$ . The type of harmonics produced depend on the response function f:

When the response function is even, the resulting signal will consist of only even harmonics of the input sine wave; 0 f , 2 f , 4 f , 6 f , … {\displaystyle 0f,2f,4f,6f,\dots }
- The fundamental is also an odd harmonic, so will not be present.
- A simple example is a full-wave rectifier.
- The $0f$ component represents the DC offset, due to the one-sided nature of even-symmetric transfer functions.
When it is odd, the resulting signal will consist of only odd harmonics of the input sine wave; 1 f , 3 f , 5 f , … {\displaystyle 1f,3f,5f,\dots }
- The output signal will be half-wave symmetric.
- A simple example is clipping in a symmetric push-pull amplifier.
When it is asymmetric, the resulting signal may contain either even or odd harmonics; 1 f , 2 f , 3 f , … {\displaystyle 1f,2f,3f,\dots }
- Simple examples are a half-wave rectifier, and clipping in an asymmetrical class-A amplifier.

This does not hold true for more complex waveforms. A sawtooth wave contains both even and odd harmonics, for instance. After even-symmetric full-wave rectification, it becomes a triangle wave, which, other than the DC offset, contains only odd harmonics.

Generalizations

Multivariate functions

Even symmetry:

A function $f:\mathbb {R} ^{n}\to \mathbb {R}$ is called even symmetric if:

f(x_{1},x_{2},\ldots ,x_{n})=f(-x_{1},-x_{2},\ldots ,-x_{n})\quad {\text{for all }}x_{1},\ldots ,x_{n}\in \mathbb {R}

Odd symmetry:

A function $f:\mathbb {R} ^{n}\to \mathbb {R}$ is called odd symmetric if:

f(x_{1},x_{2},\ldots ,x_{n})=-f(-x_{1},-x_{2},\ldots ,-x_{n})\quad {\text{for all }}x_{1},\ldots ,x_{n}\in \mathbb {R}

Complex-valued functions

The definitions for even and odd symmetry for complex-valued functions of a real argument are similar to the real case. In signal processing, a similar symmetry is sometimes considered, which involves complex conjugation.

Conjugate symmetry:

A complex-valued function of a real argument $f:\mathbb {R} \to \mathbb {C}$ is called conjugate symmetric if

f(x)={\overline {f(-x)}}\quad {\text{for all }}x\in \mathbb {R}

A complex valued function is conjugate symmetric if and only if its real part is an even function and its imaginary part is an odd function.

A typical example of a conjugate symmetric function is the cis function

x\to e^{ix}=\cos x+i\sin x

Conjugate antisymmetry:

A complex-valued function of a real argument $f:\mathbb {R} \to \mathbb {C}$ is called conjugate antisymmetric if:

f(x)=-{\overline {f(-x)}}\quad {\text{for all }}x\in \mathbb {R}

A complex valued function is conjugate antisymmetric if and only if its real part is an odd function and its imaginary part is an even function.

Finite length sequences

The definitions of odd and even symmetry are extended to N-point sequences (i.e. functions of the form $f:\left\{0,1,\ldots ,N-1\right\}\to \mathbb {R}$ ) as follows: