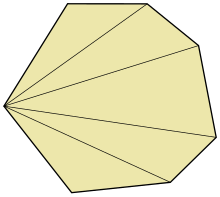
In computational geometry, a fan triangulation is a simple way to triangulate a polygon by choosing a vertex and drawing edges to all of the other vertices of the polygon. Not every polygon can be triangulated this way, so this method is usually only used for convex polygons.
Properties
Aside from the properties of all triangulations, fan triangulations have the following properties:
- All convex polygons, but not all polygons, can be fan triangulated.
- Polygons with only one concave vertex can always be fan triangulated, as long as the diagonals are drawn from the concave vertex.
- It can be known if a polygon can be fan triangulated by solving the Art gallery problem, in order to determine whether there is at least one vertex that is visible from every point in the polygon.
- The triangulation of a polygon with vertices uses diagonals, and generates triangles.
- Generating the list of triangles is trivial if an ordered list of vertices is available, and can be computed in linear time. As such, it is unnecessary to explicitly store the list of triangles, and therefore, many graphical libraries implement primitives to represent polygons based on this triangulation.
- Although this triangulation is fit for solving certain problems, such as Rasterisation, or collision detection, it may be unfit for other tasks because the origin vertex accumulates a high number of neighbors, and the internal angles of the triangulation are unevenly distributed.
vertices uses 
diagonals, and generates 
triangles.See also
References
- Loera, Jesus; Rambau, Joerg; Santos, Francisco (2010). Triangulations: Structures for Algorithms and Applications. Springer Science & Business Media. pp. 103. ISBN 9783642129711.
- O'Rourke, Joseph (1998). Computational geometry in C (2nd ed.). Cambridge, UK: Cambridge University Press. ISBN 9780521649766. OCLC 38542796.
- Segal, Mark (24 October 2016). "The OpenGL Graphics System: A Specification" (PDF). Retrieved 2 March 2017.