Misplaced Pages

In discrete mathematics and theoretical computer science, the flip distance between two triangulations of the same point set is the number of flips required to transform one triangulation into another. A flip removes an edge between two triangles in the triangulation and then adds the other diagonal in the edge's enclosing quadrilateral, forming a different triangulation of the same point set.

This problem is known to be NP-hard. However, the computational complexity of determining the flip distance between convex polygons, a special case of this problem, is unknown. Computing the flip distance between convex polygon triangulations is also equivalent to rotation distance, the number of rotations required to transform one binary tree into another.

Definition

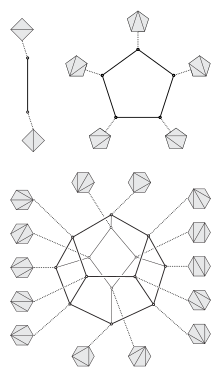
Given a family of triangulations of some geometric object, a flip is an operation that transforms one triangulation to another by removing an edge between two triangles and adding the opposite diagonal to the resulting quadrilateral. The flip distance between two triangulations is the minimum number of flips needed to transform one triangulation into another. It can also be described as the shortest path distance in a flip graph, a graph that has a vertex for each triangulation and an edge for each flip between two triangulations. Flips and flip distances can be defined in this way for several different kinds of triangulations, including triangulations of sets of points in the Euclidean plane, triangulations of polygons, and triangulations of abstract manifolds.

Feasibility

The flip distance is well-defined only if any triangulation can be converted to any other triangulation via a sequence of flips. An equivalent condition is that the flip graph must be connected.

In 1936, Klaus Wagner showed that maximal planar graphs on a sphere can be transformed to any other maximal planar graph with the same vertices through flipping. A. K. Dewdney generalized this result to triangulations on the surface of a torus while Charles Lawson to triangulations of a point set on a 2-dimensional plane.

For triangulations of a point set in dimension 5 or above, there exists examples where the flip graph is disconnected and a triangulation cannot be obtained from other triangulations via flips. Whether all flip graphs of finite 3- or 4-dimensional point sets are connected is an open problem.

Diameter of the flip graph

The maximum number of flips required to transform a triangulation into another is the diameter of the flip graph. The diameter of the flip graph of a convex ${\displaystyle n}$-gon has been obtained by Daniel Sleator, Robert Tarjan, and William Thurston when ${\displaystyle n}$ is sufficiently large and by Lionel Pournin for all ${\displaystyle n}$. This diameter is equal to ${\displaystyle 2n-10}$ when ${\displaystyle n\geq 13}$.

The diameter of other flip graphs has been studied. For instance Klaus Wagner provided a quadratic upper bound on the diameter of the flip graph of a set of ${\displaystyle n}$ unmarked points on the sphere. The current upper bound on the diameter is ${\displaystyle 5n-23}$, while the best-known lower bound is ${\displaystyle 7n/3+\Theta (1)}$. The diameter of the flip graphs of arbitrary topological surfaces with boundary has also been studied and their exact value is known in several cases.

Equivalence with other problems

The flip distance between triangulations of a convex polygon is equivalent to the rotation distance between two binary trees.

Computational complexity

Computing the flip distance between triangulations of a point set is both NP-complete and APX-hard. However, it is fixed-parameter tractable (FPT), and several FPT algorithms that run in exponential time have been proposed.

Computing the flip distance between triangulations of a simple polygon is also NP-hard.

The complexity of computing the flip distance between triangulations of a convex polygon remains an open problem.

Algorithms

Let n be the number of points in the point set and k be the flip distance. The current best FPT algorithm runs in ${\displaystyle O(n+k\cdot 32^{k})}$. A faster FPT algorithm exists for the flip distance between convex polygon triangulations; it has time complexity ${\displaystyle O(3.82^{k})}$

If no five points of a point set form an empty pentagon, there exists a ${\displaystyle O(n^{2})}$ algorithm for the flip distance between triangulations of this point set.

See also

• Associahedron
• Flip graph
• Rotation distance
• Tamari lattice

References

1. ^ Eppstein, David (2010). "Happy endings for flip graphs". Journal of Computational Geometry. 1 (1): Vol. 1 No. 1 (2010). doi:10.20382/JOCG.V1I1A2.
2. ^ Dewdney, A.K. (1973). "Wagner's theorem for Torus graphs". Discrete Mathematics. 4 (2). Elsevier BV: 139–149. doi:10.1016/0012-365x(73)90076-9. ISSN 0012-365X.
3. ^ Santos, Francisco (2005-04-02). "Non-connected toric Hilbert schemes". Mathematische Annalen. 332 (3). Springer Science and Business Media LLC: 645–665. arXiv:math/0204044. doi:10.1007/s00208-005-0643-5. ISSN 0025-5831.
4. ^ Wagner, K. (1936). "Bemerkungen zum Vierfarbenproblem". Jahresbericht der Deutschen Mathematiker-Vereinigung. 46: 26–32. ISSN 0012-0456.
5. Lawson, Charles L. (1972). "Transforming triangulations". Discrete Mathematics. 3 (4). Elsevier BV: 365–372. doi:10.1016/0012-365x(72)90093-3. ISSN 0012-365X.
6. Santos, Francisco (2000). "A Point Set Whose Space of Triangulations is Disconnected". Journal of the American Mathematical Society. 13 (3). American Mathematical Society: 611–637. doi:10.1090/S0894-0347-00-00330-1. hdl:10902/2584. ISSN 0894-0347. JSTOR 2646121.
7. De Loera, Jesús A.; Rambau, Jörg; Santos, Francisco (2010). Triangulations, Structures for Algorithms and Applications. Algorithms and Computation in Mathematics. Vol. 25. Springer.
8. ^ Sleator, Daniel D.; Tarjan, Robert E.; Thurston, William P. (1988). "Rotation distance, triangulations, and hyperbolic geometry". Journal of the American Mathematical Society. 1 (3). American Mathematical Society (AMS): 647–681. doi:10.1090/s0894-0347-1988-0928904-4. ISSN 0894-0347.
9. Pournin, Lionel (2014), "The diameter of associahedra", Advances in Mathematics, 259: 13–42, arXiv:1207.6296, doi:10.1016/j.aim.2014.02.035, MR 3197650
10. Cardinal, Jean; Hoffmann, Michael; Kusters, Vincent; Tóth, Csaba D.; Wettstein, Manuel (2018). "Arc diagrams, flip distances, and Hamiltonian triangulations". Computational Geometry. 68: 206–225. arXiv:1611.02541. doi:10.1016/j.comgeo.2017.06.001.
11. Frati, Fabrizio (2017). "A Lower Bound on the Diameter of the Flip Graph". Electronic Journal of Combinatorics. 24 (1): P1.43. arXiv:1508.03473. doi:10.37236/5489.
12. Parlier, Hugo; Pournin, Lionel (2017). "Flip-graph moduli spaces of filling surfaces". Journal of the European Mathematical Society. 19 (9): 2697–2737. arXiv:1407.1516. doi:10.4171/JEMS/726.
13. Parlier, Hugo; Pournin, Lionel (2018). "Modular flip-graphs of one holed surfaces". European Journal of Combinatorics. 67: 158–173. arXiv:1510.07664. doi:10.1016/j.ejc.2017.07.003.
14. Parlier, Hugo; Pournin, Lionel (2018). "Once punctured disks, non-convex polygons, and pointihedra". Annals of Combinatorics. 22 (3): 619–640. arXiv:1602.04576. doi:10.1007/s00026-018-0393-1.
15. Lubiw, Anna; Pathak, Vinayak (2015). "Flip distance between two triangulations of a point set is NP-complete". Computational Geometry. 49. Elsevier BV: 17–23. arXiv:1205.2425. doi:10.1016/j.comgeo.2014.11.001. ISSN 0925-7721.
16. Pilz, Alexander (2014). "Flip distance between triangulations of a planar point set is APX-hard". Computational Geometry. 47 (5). Elsevier BV: 589–604. arXiv:1206.3179. doi:10.1016/j.comgeo.2014.01.001. ISSN 0925-7721.
17. ^ Feng, Qilong; Li, Shaohua; Meng, Xiangzhong; Wang, Jianxin (2021). "An fpt2 FPT algorithm for the flip distance problem". Information and Computation. 281. Elsevier BV: 104708. arXiv:1910.06185. doi:10.1016/j.ic.2021.104708. ISSN 0890-5401.
18. Kanj, Iyad; Sedgwick, Eric; Xia, Ge (2017-02-10). "Computing the Flip Distance Between Triangulations". Discrete & Computational Geometry. 58 (2). Springer Science and Business Media LLC: 313–344. arXiv:1407.1525. doi:10.1007/s00454-017-9867-x. ISSN 0179-5376.
19. Aichholzer, Oswin; Mulzer, Wolfgang; Pilz, Alexander (2015-06-11). "Flip Distance Between Triangulations of a Simple Polygon is NP-Complete". Discrete & Computational Geometry. 54 (2). Springer Science and Business Media LLC: 368–389. arXiv:1209.0579. doi:10.1007/s00454-015-9709-7. ISSN 0179-5376.
20. ^ Li, Haohong; Xia, Ge (2023). "An 𝒪(3.82^k) Time FPT Algorithm for Convex Flip Distance". Schloss Dagstuhl - Leibniz-Zentrum für Informatik: 44:1–44:14. doi:10.4230/LIPICS.STACS.2023.44. Retrieved 2023-11-08.

• Triangulation (geometry)
• Reconfiguration