Misplaced Pages

Focal conics

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Pairs of conic sections in geometry
Definition of focal conics
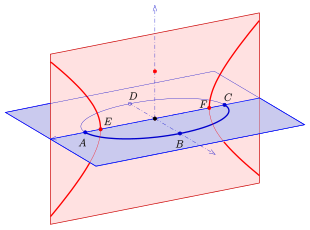
A,C: vertices of the ellipse and foci of the hyperbola
E,F: foci of the ellipse and vertices of the hyperbola
Focal conics: two parabolas
A: vertex of the red parabola and focus of the blue parabola
F: focus of the red parabola and vertex of the blue parabola

In geometry, focal conics are a pair of curves consisting of either

  • an ellipse and a hyperbola, where the hyperbola is contained in a plane, which is orthogonal to the plane containing the ellipse. The vertices of the hyperbola are the foci of the ellipse and its foci are the vertices of the ellipse (see diagram).

or

  • two parabolas, which are contained in two orthogonal planes and the vertex of one parabola is the focus of the other and vice versa.

Focal conics play an essential role answering the question: "Which right circular cones contain a given ellipse or hyperbola or parabola (see below)".

Focal conics are used as directrices for generating Dupin cyclides as canal surfaces in two ways.

Focal conics can be seen as degenerate focal surfaces: Dupin cyclides are the only surfaces, where focal surfaces collapse to a pair of curves, namely focal conics.

In Physical chemistry focal conics are used for describing geometrical properties of liquid crystals.

One should not mix focal conics with confocal conics. The latter ones have all the same foci.

Equations and parametric representations

Ellipse and hyperbola

Equations

If one describes the ellipse in the x-y-plane in the common way by the equation

x 2 a 2 + y 2 b 2 = 1 , {\displaystyle {\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2}}}=1\;,}

then the corresponding focal hyperbola in the x-z-plane has equation

x 2 c 2 − z 2 b 2 = 1 , {\displaystyle {\frac {x^{2}}{c^{2}}}-{\frac {z^{2}}{b^{2}}}=1\;,}

where c {\displaystyle c} is the linear eccentricity of the ellipse with c 2 = a 2 − b 2 . {\displaystyle \;c^{2}=a^{2}-b^{2}\;.}

Parametric representations
ellipse: u → ( φ ) = ( a cos ⁡ φ , b sin ⁡ φ , 0 ) T   {\displaystyle \quad {\vec {u}}(\varphi )=(a\cos \varphi ,b\sin \varphi ,0)^{T}\ } and
hyperbola:   v → ( ψ ) = ( c cosh ⁡ ψ , 0 , b sinh ⁡ ψ ) T   . {\displaystyle \ {\vec {v}}(\psi )=(c\cosh \psi ,0,b\sinh \psi )^{T}\ .}

Two parabolas

Two parabolas in the x-y-plane and in the x-z-plane:

1. parabola:   y 2 = p 2 − 2 p x   {\displaystyle \ y^{2}=p^{2}-2px\ } and
2. parabola:   z 2 = 2 p x   . {\displaystyle \ z^{2}=2px\ .}

with p {\displaystyle p} the semi-latus rectum of both the parabolas.

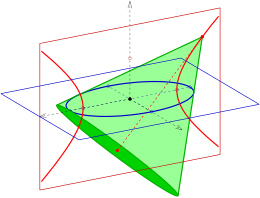
Right circular cone (green) through an ellipse (blue)

Right circular cones through an ellipse

  • The apices of the right circular cones through a given ellipse lie on the focal hyperbola belonging to the ellipse.
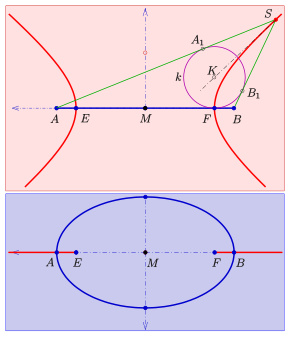
Right circular cones through an ellipse
Proof

Given: Ellipse with vertices A , B {\displaystyle A,B} and foci E , F {\displaystyle E,F} and a right circular cone with apex S {\displaystyle S} containing the ellipse (see diagram).

Because of symmetry the axis of the cone has to be contained in the plane through the foci, which is orthogonal to the ellipse's plane. There exists a Dandelin sphere k {\displaystyle k} , which touches the ellipse's plane at the focus F {\displaystyle F} and the cone at a circle. From the diagram and the fact that all tangential distances of a point to a sphere are equal one gets:

| A S | = | A A 1 | + | A 1 S | = | A F | + | B 1 S | {\displaystyle |AS|=|AA_{1}|+|A_{1}S|=|AF|+|B_{1}S|}
| B S | = | B B 1 | + | B 1 S | = | B F | + | B 1 S | {\displaystyle |BS|=|BB_{1}|+|B_{1}S|=|BF|+|B_{1}S|}

Hence:

| A S | − | B S | = | A F | − | B F | = | E F | = {\displaystyle |AS|-|BS|=|AF|-|BF|=|EF|=} const.

and the set of all possible apices lie on the hyperbola with the vertices E , F {\displaystyle E,F} and the foci A , B {\displaystyle A,B} .

Analogously one proves the cases, where the cones contain a hyperbola or a parabola.

References

  1. Müller- Kruppa, S. 104
  2. Glaeser-Stachel-Odehnal, p. 137
  3. Felix Klein: Vorlesungen Über Höhere Geometrie, Herausgeber: W. Blaschke, Richard Courant, Springer-Verlag, 2013, ISBN 3642498485, S. 58.
  4. Glaeser-Stachel-Odehnal: p. 147
  5. D. Hilbert, S. Cohn-Vossen:Geometry and the Imagination, Chelsea Publishing Company, 1952, p. 218.
  6. Thomas Andrew Waigh: The Physics of Living Processes, Verlag John Wiley & Sons, 2014, ISBN 1118698274, p. 128.
  7. Glaeser-Stachel-Odehnal p. 139
  • Georg Glaeser, Hellmuth Stachel, Boris Odehnal: The Universe of Conics, Springer, 2016, ISBN 3662454505.
  • E. Müller, E. Kruppa: Lehrbuch der darstellenden Geomelrie, Springer-Verlag, Wien, 1961, ISBN 978-3-211-80589-3.
Category: