Misplaced Pages

Network synthesis is a design technique for linear electrical circuits. Synthesis starts from a prescribed impedance function of frequency or frequency response and then determines the possible networks that will produce the required response. The technique is to be compared to network analysis in which the response (or other behaviour) of a given circuit is calculated. Prior to network synthesis, only network analysis was available, but this requires that one already knows what form of circuit is to be analysed. There is no guarantee that the chosen circuit will be the closest possible match to the desired response, nor that the circuit is the simplest possible. Network synthesis directly addresses both these issues. Network synthesis has historically been concerned with synthesising passive networks, but is not limited to such circuits.

The field was founded by Wilhelm Cauer after reading Ronald M. Foster's 1924 paper A reactance theorem. Foster's theorem provided a method of synthesising LC circuits with arbitrary number of elements by a partial fraction expansion of the impedance function. Cauer extended Foster's method to RC and RL circuits, found new synthesis methods, and methods that could synthesise a general RLC circuit. Other important advances before World War II are due to Otto Brune and Sidney Darlington. In the 1940s Raoul Bott and Richard Duffin published a synthesis technique that did not require transformers in the general case (the elimination of which had been troubling researchers for some time). In the 1950s, a great deal of effort was put into the question of minimising the number of elements required in a synthesis, but with only limited success. Little was done in the field until the 2000s when the issue of minimisation again became an active area of research, but as of 2023, is still an unsolved problem.

A primary application of network synthesis is the design of network synthesis filters but this is not its only application. Amongst others are impedance matching networks, time-delay networks, directional couplers, and equalisation. In the 2000s, network synthesis began to be applied to mechanical systems as well as electrical, notably in Formula One racing.

Overview

Network synthesis is all about designing an electrical network that behaves in a prescribed way without any preconception of the network form. Typically, an impedance is required to be synthesised using passive components. That is, a network consisting of resistances (R), inductances (L) and capacitances (C). Such networks always have an impedance, denoted ${\displaystyle Z(s)}$, in the form of a rational function of the complex frequency variable s. That is, the impedance is the ratio of two polynomials in s.

There are three broad areas of study in network synthesis; approximating a requirement with a rational function, synthesising that function into a network, and determining equivalents of the synthesised network.

Approximation

The idealised prescribed function will rarely be capable of being exactly described by polynomials. It is therefore not possible to synthesise a network to exactly reproduce it. A simple, and common, example is the brick-wall filter. This is the ideal response of a low-pass filter but its piecewise continuous response is impossible to represent with polynomials because of the discontinuities. To overcome this difficulty, a rational function is found that closely approximates the prescribed function using approximation theory. In general, the closer the approximation is required to be, the higher the degree of the polynomial and the more elements will be required in the network.

There are many polynomials and functions used in network synthesis for this purpose. The choice depends on which parameters of the prescribed function the designer wishes to optimise. One of the earliest used was Butterworth polynomials which results in a maximally flat response in the passband. A common choice is the Chebyshev approximation in which the designer specifies how much the passband response can deviate from the ideal in exchange for improvements in other parameters. Other approximations are available for optimising time delay, impedance matching, roll-off, and many other requirements.

Realisation

Given a rational function, it is usually necessary to determine whether the function is realisable as a discrete passive network. All such networks are described by a rational function, but not all rational functions are realisable as a discrete passive network. Historically, network synthesis was concerned exclusively with such networks. Modern active components have made this limitation less relevant in many applications, but at the higher radio frequencies passive networks are still the technology of choice. There is a simple property of rational functions that predicts whether the function is realisable as a passive network. Once it is determined that a function is realisable, there a number of algorithms available that will synthesise a network from it.

Equivalence

A network realisation from a rational function is not unique. The same function may realise many equivalent networks. It is known that affine transformations of the impedance matrix formed in mesh analysis of a network are all impedance matrices of equivalent networks (further information at Analogue filter § Realisability and equivalence). Other impedance transformations are known, but whether there are further equivalence classes that remain to be discovered is an open question.

A major area of research in network synthesis has been to find the realisation which uses the minimum number of elements. This question has not been fully solved for the general case, but solutions are available for many networks with practical applications.

History

The field of network synthesis was founded by German mathematician and scientist Wilhelm Cauer (1900–1945). The first hint towards a theory came from American mathematician Ronald M. Foster (1896–1998) when he published A reactance theorem in 1924. Cauer immediately recognised the importance of this work and set about generalising and extending it. His thesis in 1926 was on "The realisation of impedances of prescibed frequency dependence" and is the beginning of the field. Cauer's most detailed work was done during World War II, but he was killed shortly before the end of the war. His work could not be widely published during the war, and it was not until 1958 that his family collected his papers and published them for the wider world. Meanwhile, progress had been made in the United States based on Cauer's pre-war publications and material captured during the war.

English self-taught mathematician and scientist Oliver Heaviside (1850–1925) was the first to show that the impedance of an RLC network was always a rational function of a frequency operator, but provided no method of realising a network from a rational function. Cauer found a necessary condition for a rational function to be realisable as a passive network. South African Otto Brune (1901–1982) later coined the term positive-real function (PRF) for this condition. Cauer postulated that PRF was a necessary and sufficient condition but could not prove it, and suggested it as a research project to Brune, who was his grad student in the United States at the time. Brune published the missing proof in his 1931 doctoral thesis.

Foster's realisation was limited to LC networks and was in one of two forms; either a number of series LC circuits in parallel, or a number of parallel LC circuits in series. Foster's method was to expand ${\displaystyle Z(s)}$ into partial fractions. Cauer showed that Foster's method could be extended to RL and RC networks. Cauer also found another method; expanding ${\displaystyle Z(s)}$ as a continued fraction which results in a ladder network, again in two possible forms. In general, a PRF will represent an RLC network; with all three kinds of element present the realisation is trickier. Both Cauer and Brune used ideal transformers in their realisations of RLC networks. Having to include transformers is undesirable in a practical implementation of a circuit.

A method of realisation that did not require transformers was provided in 1949 by Hungarian-American mathematician Raoul Bott (1923–2005) and American physicist Richard Duffin (1909–1996). The Bott and Duffin method provides an expansion by repeated application of Richards' theorem, a 1947 result due to American physicist and applied mathematician Paul I. Richards (1923–1978). The resulting Bott-Duffin networks have limited practical use (at least for rational functionals of high degree) because the number of components required grows exponentially with the degree. A number of variations of the original Bott-Duffin method all reduce the number of elements in each section from six to five, but still with exponentially growing overall numbers. Papers achieving this include Pantell (1954), Reza (1954), Storer (1954) and Fialkow & Gest (1955). As of 2010, there has been no further significant advance in synthesising rational functions.

In 1939, American electrical engineer Sidney Darlington showed that any PRF can be realised as a two-port network consisting only of L and C elements and terminated at its output with a resistor. That is, only one resistor is required in any network, the remaining components being lossless. The theorem was independently discovered by both Cauer and Giovanni Cocci. The corollary problem, to find a synthesis of PRFs using R and C elements with only one inductor, is an unsolved problem in network theory. Another unsolved problem is finding a proof of Darlington's conjecture (1955) that any RC 2-port with a common terminal can be realised as a series-parallel network. An important consideration in practical networks is to minimise the number of components, especially the wound components—inductors and transformers. Despite great efforts being put into minimisation, no general theory of minimisation has ever been discovered as it has for the Boolean algebra of digital circuits.

Cauer used elliptic rational functions to produce approximations to ideal filters. A special case of elliptic rational functions is the Chebyshev polynomials due to Pafnuty Chebyshev (1821–1894) and is an important part of approximation theory. Chebyshev polynomials are widely used to design filters. In 1930, British physicist Stephen Butterworth (1885–1958) designed the Butterworth filter, otherwise known as the maximally-flat filter, using Butterworth polynomials. Butterworth's work was entirely independent of Cauer, but it was later found that the Butterworth polynomials were a limiting case of the Chebyshev polynomials. Even earlier (1929) and again independently, American engineer and scientist Edward Lawry Norton (1898–1983) designed a maximally-flat mechanical filter with a response entirely analogous to Butterworth's electrical filter.

In the 2000s, interest in further developing network synthesis theory was given a boost when the theory started to be applied to large mechanical systems. The unsolved problem of minimisation is much more important in the mechanical domain than the electrical due to the size and cost of components. In 2017, researchers at the University of Cambridge, limiting themselves to considering biquadratic rational functions, determined that Bott-Duffin realisations of such functions for all series-parallel networks and most arbitrary networks had the minimum number of reactances (Hughes, 2017). They found this result surprising as it showed that the Bott-Duffin method was not quite so non-minimal as previously thought. This research partly centred on revisiting the Ladenheim Catalogue. This is an enumeration of all distinct RLC networks with no more than two reactances and three resistances. Edward Ladenheim carried out this work in 1948 while a student of Foster. The relevance of the catalogue is that all these networks are realised by biquadratic functions.

Applications

The single most widely used application of network synthesis is in the design of signal processing filters. The modern designs of such filters are almost always some form of network synthesis filter.

Another application is the design of impedance matching networks. Impedance matching at a single frequency requires only a trivial network—usually one component. Impedance matching over a wide band, however, requires a more complex network, even in the case that the source and load resistances do not vary with frequency. Doing this with passive elements and without the use of transformers results in a filter-like design. Furthermore, if the load is not a pure resistance then it is only possible to achieve a perfect match at a number of discrete frequencies; the match over the band as a whole must be approximated. The designer first prescribes the frequency band over which the matching network is to operate, and then designs a band-pass filter for that band. The only essential difference between a standard filter and a matching network is that the source and load impedances are not equal.

There are differences between filters and matching networks in which parameters are important. Unless the network has a dual function, the designer is not too concerned over the behaviour of the impedance matching network outside the passband. It does not matter if the transition band is not very narrow, or that the stopband has poor attenuation. In fact, trying to improve the bandwidth beyond what is strictly necessary will detract from the accuracy of the impedance match. With a given number of elements in the network, narrowing the design bandwidth improves the matching and vice versa. The limitations of impedance matching networks were first investigated by American engineer and scientist Hendrik Wade Bode in 1945, and the principle that they must necessarily be filter-like was established by Italian-American computer scientist Robert Fano in 1950. One parameter in the passband that is usually set for filters is the maximum insertion loss. For impedance matching networks, a better match can be obtained by also setting a minimum loss. That is, the gain never rises to unity at any point.

Time-delay networks can be designed by network synthesis with filter-like structures. It is not possible to design a delay network that has a constant delay at all frequencies in a band. An approximation to this behaviour must be used limited to a prescribed bandwidth. The prescribed delay will occur at most at a finite number of spot frequencies. The Bessel filter has maximally-flat time-delay.

The application of network synthesis is not limited to the electrical domain. It can be applied to systems in any energy domain that can be represented as a network of linear components. In particular, network synthesis has found applications in mechanical networks in the mechanical domain. Consideration of mechanical network synthesis led Malcolm C. Smith to propose a new mechanical network element, the inerter, which is analogous to the electrical capacitor. Mechanical components with the inertance property have found an application in the suspensions of Formula One racing cars.

Synthesis techniques

Synthesis begins by choosing an approximation technique that delivers a rational function approximating the required function of the network. If the function is to be implemented with passive components, the function must also meet the conditions of a positive-real function (PRF). The synthesis technique used depends in part on what form of network is desired, and in part how many kinds of elements are needed in the network. A one-element-kind network is a trivial case, reducing to an impedance of a single element. A two-element-kind network (LC, RC, or RL) can be synthesised with Foster or Cauer synthesis. A three-element-kind network (an RLC network) requires more advanced treatment such as Brune or Bott-Duffin synthesis.

Which, and how many kinds of, elements are required can be determined by examining the poles and zeroes (collectively called critical frequencies) of the function. The requirement on the critical frequencies is given for each kind of network in the relevant sections below.

Foster synthesis

Foster's synthesis, in its original form, can be applied only to LC networks. A PRF represents a two-element-kind LC network if the critical frequencies of ${\displaystyle Z(s)}$ all exist on the ${\displaystyle i\omega }$ axis of the complex plane of ${\displaystyle s=\sigma +i\omega }$ (the s-plane) and will alternate between poles and zeroes. There must be a single critical frequency at the origin and at infinity, all the rest must be in conjugate pairs. ${\displaystyle Z(s)}$ must be the ratio of an even and odd polynomial and their degrees must differ by exactly one. These requirements are a consequence of Foster's reactance theorem.

Foster I form

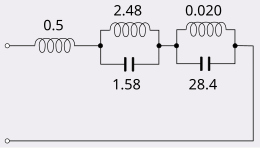
Foster's first form (Foster I form) synthesises ${\displaystyle Z(s)}$ as a set of parallel LC circuits in series. For example,

${\displaystyle Z(s)={\frac {9s^{5}+30s^{3}+24s}{18s^{4}+36s^{2}+8}}}$

can be expanded into partial fractions as,

${\displaystyle Z(s)={s \over 2}+{\frac {(25+11{\sqrt {5}})s}{5(9+3{\sqrt {5}})s^{2}+20}}+{\frac {(25-11{\sqrt {5}})s}{5(9-3{\sqrt {5}})s^{2}+20}}\approx {s \over 2}+{\frac {2.48s}{3.93s^{2}+1}}+{\frac {0.020s}{0.573s^{2}+1}}}$

The first term represents a series inductor, a consequence of ${\displaystyle Z(s)}$ having a pole at infinity. If it had had a pole at the origin, that would represent a series capacitor. The remaining two terms each represent conjugate pairs of poles on the ${\displaystyle i\omega }$ axis. Each of these terms can be synthesised as a parallel LC circuit by comparison with the impedance expression for such a circuit,

${\displaystyle Z_{LC}(s)={\frac {Ls}{LCs^{2}+1}}}$

The resulting circuit is shown in the figure.

Foster II form

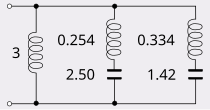
Foster II form synthesises ${\displaystyle Z(s)}$ as a set of series LC circuits in parallel. The same method of expanding into partial fractions is used as for Foster I form, but applied to the admittance, ${\displaystyle Y(s)}$, instead of ${\displaystyle Z(s)}$. Using the same example PRF as before,

${\displaystyle Y(s)={1 \over Z(s)}={\frac {18s^{4}+36s^{2}+8}{9s^{5}+30s^{3}+24s}}}$

Expanded in partial fractions,

${\displaystyle Y(s)\simeq {1 \over 3s}+{\frac {2.498s}{0.6346s^{2}+1}}+{\frac {1.415s}{0.4719s^{2}+1}}}$

The first term represents a shunt inductor, a consequence of ${\displaystyle Y(s)}$ having a pole at the origin (or, equivalently, ${\displaystyle Z(s)}$ has a zero at the origin). If it had had a pole at infinity, that would represent a shunt capacitor. The remaining two terms each represent conjugate pairs of poles on the ${\displaystyle i\omega }$ axis. Each of these terms can be synthesised as a series LC circuit by comparison with the admittance expression for such a circuit,

${\displaystyle Y_{LC}(s)={\frac {Cs}{LCs^{2}+1}}}$

The resulting circuit is shown in the figure.

Extension to RC or RL networks

Foster synthesis can be extended to any two-element-kind network. For instance, the partial fraction terms of an RC network in Foster I form will each represent an R and C element in parallel. In this case, the partial fractions will be of the form,

${\displaystyle Z_{RC}(s)={\frac {R}{RCs+1}}}$

Other forms and element kinds follow by analogy. As with an LC network, The PRF can be tested to see if it is an RC or RL network by examining the critical frequencies. The critical frequencies must all be on the negative real axis and alternate between poles and zeroes, and there must be an equal number of each. If the critical frequency nearest, or at, the origin is a pole, then the PRF is an RC network if it represents a ${\displaystyle Z(s)}$, or it is an RL network if it represents a ${\displaystyle Y(s)}$. Vice versa if the critical frequency nearest, or at, the origin is a zero. These extensions of the theory also apply to the Cauer forms described below.

Immittance

In the Foster synthesis above, the expansion of the function is the same procedure in both the Foster I form and Foster II form. It is convenient, especially in theoretical works, to treat them together as an immittance rather than separately as either an impedance or an admittance. It is only necessary to declare whether the function represents an impedance or an admittance at the point that an actual circuit needs to be realised. Immittance can also be used in the same way with the Cauer I and Cauer II forms and other procedures.

Cauer synthesis

Cauer synthesis is an alternative synthesis to Foster synthesis and the conditions that a PRF must meet are exactly the same as Foster synthesis. Like Foster synthesis, there are two forms of Cauer synthesis, and both can be extended to RC and RL networks.

Cauer I form

The Cauer I form expands ${\displaystyle Z(s)}$ into a continued fraction. Using the same example as used for the Foster I form,

${\displaystyle Z(s)=0.5s+{\cfrac {1}{1.5s+{\cfrac {1}{2s+{\cfrac {1}{1.5s+{\cfrac {1}{0.5s}}}}}}}}}$

or, in more compact notation,

${\displaystyle Z(s)=.}$

The terms of this expansion can be directly implemented as the component values of a ladder network as shown in the figure. The given PRF may have a denominator that has a greater degree than the numerator. In such cases, the multiplicative inverse of the function is expanded instead. That is, if the function represents ${\displaystyle Z(s)}$, then ${\displaystyle Y(s)}$ is expanded instead and vice versa.

Cauer II form

Cauer II form expands ${\displaystyle Z(s)}$ in exactly the same way as Cauer I form except that lowest degree term is extracted first in the continued fraction expansion rather than the highest degree term as is done in Cauer I form. The example used for the Cauer I form and the Foster forms when expanded as a Cauer II form results in some elements having negative values. This particular PRF, therefore, cannot be realised in passive components as a Cauer II form without the inclusion of transformers or mutual inductances.

The essential reason that the example ${\displaystyle Z(s)}$ cannot be realised as a Cauer II form is that this form has a high-pass topology. The first element extracted in the continued fraction is a series capacitor. This makes it impossible for the zero of ${\displaystyle Z(s)}$ at the origin to be realised. The Cauer I form, on the other hand, has a low-pass topology and naturally has a zero at the origin. However, the ${\displaystyle Y(s)}$ of this function can be realised as a Cauer II form since the first element extracted is a shunt inductor. This gives a pole at the origin for ${\displaystyle Y(s)}$, but that translates to the necessary zero at the origin for ${\displaystyle Z(s)}$. The continued fraction expansion is,

${\displaystyle Y(s)\simeq \left}$

and the realised network is shown in the figure.

Brune synthesis

The Brune synthesis can synthesise any arbitrary PRF, so in general will result in a 3-element-kind (i.e. RLC) network. The poles and zeroes can lie anywhere in the left-hand half of the complex plane. The Brune method starts with some preliminary steps to eliminate critical frequencies on the imaginary axis as in the Foster method. These preliminary steps are sometimes called the Foster preamble. There is then a cycle of steps to produce a cascade of Brune sections.

Removal of critical frequencies on the imaginary axis

Poles and zeroes on the ${\displaystyle j\omega }$ axis represent L and C elements that can be extracted from the PRF. Specifically,

• a pole at the origin represents a series capacitor
• a pole at infinity represents a series inductance
• a zero at the origin represents a shunt inductor
• a zero at infinity represents a shunt capacitor
• a pair of poles at ${\displaystyle s=\pm i\omega _{c}}$ represents a parallel LC circuit of resonant frequency ${\displaystyle \omega _{c}}$ in series
• a pair of zeroes at ${\displaystyle s=\pm i\omega _{c}}$ represents a series LC circuit of resonant frequency ${\displaystyle \omega _{c}}$ in shunt

After these extractions, the remainder PRF has no critical frequencies on the imaginary axis and is known as a minimum reactance, minimum susceptance function. Brune synthesis proper begins with such a function.

Broad outline of method

The essence of the Brune method is to create a conjugate pair of zeroes on the ${\displaystyle i\omega }$ axis by extracting the real and imaginary parts of the function at that frequency, and then extract the pair of zeroes as a resonant circuit. This is the first Brune section of the synthesised network. The resulting remainder is another minimum reactance function that is two degrees lower. The cycle is then repeated, each cycle producing one more Brune section of the final network until just a constant value (a resistance) remains. The Brune synthesis is canonical, that is, the number of elements in the final synthesised network is equal to the number of arbitrary coefficients in the impedance function. The number of elements in the synthesised circuit cannot therefore be reduced any further.

Removal of minimum resistance

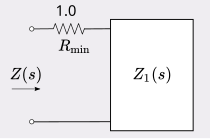
A minimum reactance function will have a minimum real part, ${\displaystyle R_{\text{min}}}$, at some frequency ${\displaystyle \omega _{0}}$. This resistance can be extracted from the function leaving a remainder of another PRF called a minimum positive-real function, or just minimum function. For example, the minimum reactance function

${\displaystyle Z(s)={\frac {3s^{2}+3s+6}{2s^{2}+s+2}}}$

has ${\displaystyle \omega _{\text{min}}={\sqrt {2}}}$ and ${\displaystyle R_{\text{min}}=1}$. The minimum function, ${\displaystyle Z_{1}(s)}$, is therefore,

${\displaystyle Z_{1}(s)=Z(s)-R_{\text{min}}={\frac {s^{2}+2s+4}{2s^{2}+s+2}}}$

Removal of a negative inductance or capacitance

Since ${\displaystyle Z_{1}(i\omega _{0})}$ has no real part, we can write,

${\displaystyle Z_{1}(i\omega _{0})=iX\ .}$

For the example function,

${\displaystyle Z_{1}(i\omega _{0})=-i{\sqrt {2}}=iX\ .}$

In this case, ${\displaystyle X}$ is negative, and we interpret it as the reactance of a negative-valued inductor, ${\displaystyle L_{1}}$. Thus,

${\displaystyle iX=i\omega _{0}L_{1}}$ and

${\displaystyle L_{1}=-1}$

after substituting in the values of ${\displaystyle \omega _{0}}$ and ${\displaystyle iX}$. This inductance is then extracted from ${\displaystyle Z_{1}(s)}$, leaving another PRF, ${\displaystyle Z_{2}(s)}$,

${\displaystyle Z_{2}(s)=Z_{1}(s)-sL_{1}={\frac {2s^{3}+2s^{2}+4s+4}{2s^{2}+s+2}}\ .}$

The reason for extracting a negative value is because ${\displaystyle -sL_{1}}$ is a PRF, which it would not be if ${\displaystyle L_{1}}$ were positive. This guarantees that ${\displaystyle Z_{2}(s)}$ will also be PRF (because the sum of two PRFs is also PRF). For cases where ${\displaystyle X}$ is a positive value, the admittance function is used instead and a negative capacitance is extracted. How these negative values are implemented is explained in a later section.

Removal of a conjugate pair of zeroes

Both the real and imaginary parts of ${\displaystyle Z(i\omega _{0})}$ have been removed in previous steps. This leaves a pair of zeroes in ${\displaystyle Z_{2}(s)}$ at ${\displaystyle \pm i\omega _{0}}$ as shown by factorising the example function;

${\displaystyle Z_{2}(s)={\frac {2s^{3}+2s^{2}+4s+4}{2s^{2}+s+2}}={\frac {(s^{2}+2)(2s+2)}{2s^{2}+s+2}}\ .}$

Since such a pair of zeroes represents a shunt resonant circuit, we extract it as a pair of poles from the admittance function,

${\displaystyle {\begin{aligned}Y_{2}(s)&={1 \over Z_{2}(s)}={\frac {2s^{2}+s+2}{(s^{2}+2)(2s+2)}}\\&={1 \over {2s+2}}+{\frac {s/2}{s^{2}+2}}\\&=Y_{3}(s)+{\frac {s/2}{s^{2}+2}}\\\end{aligned}}}$

The rightmost term is the extracted resonant circuit with ${\displaystyle L_{2}=2}$ and ${\displaystyle C_{2}=1/4}$. The network synthesised so far is shown in the figure.

Removal of a pole at infinity

${\displaystyle Z_{3}(s)}$ must have a pole at infinity, since one was created there by the extraction of a negative inductance. This pole can now be extracted as a positive inductance.

${\displaystyle Z_{3}(s)={1 \over Y_{3}(s)}=2s+2=Z_{4}(s)+2s.}$

Thus ${\displaystyle L_{3}=2}$ as shown in the figure.

Replacing negative inductance with a transformer

The negative inductance cannot be implemented directly with passive components. However, the "tee" of inductors can be converted into mutually coupled inductors which absorbs the negative inductance. With a coupling coefficient of unity (tightly coupled) the mutual inductance, ${\displaystyle M}$, in the example case is 2.0.

Rinse and repeat

In general, ${\displaystyle Z_{4}(s)}$ will be another minimum reactance function and the Brune cycle is then repeated to extract another Brune section In the example case, the original PRF was of degree 2, so after reducing it by two degrees, only a constant term is left which, trivially, synthesises as a resistance.

Positive X

In step two of the cycle it was mentioned that a negative element value must be extracted in order to guarantee a PRF remainder. If ${\displaystyle X}$ is positive, the element extracted must be a shunt capacitor instead of a series inductor if the element is to be negative. It is extracted from the admittance ${\displaystyle Y_{1}(s)}$ instead of the impedance ${\displaystyle Z_{1}(s)}$. The circuit topology arrived at in step four of the cycle is a Π (pi) of capacitors plus an inductor instead of a tee of inductors plus a capacitor. It can be shown that this Π of capacitors plus inductor is an equivalent circuit of the tee of inductors plus capacitor. Thus, it is permissible to extract a positive inductance and then proceed as though ${\displaystyle Z_{2}(s)}$ were PRF, even though it is not. The correct result will still be arrived at and the remainder function will be PRF so can be fed into the next cycle.

Bott-Duffin synthesis

The Bott-Duffin synthesis begins as with the Brune synthesis by removing all poles and zeroes on the ${\displaystyle i\omega }$ axis. Then Richards' theorem is invoked, which states for,

${\displaystyle R(s)={\frac {kZ(s)-sZ(k)}{kZ(k)-sZ(s)}}}$

if ${\displaystyle Z(s)}$ is a PRF then ${\displaystyle R(s)}$ is a PRF for all real, positive values of ${\displaystyle k}$.

Making ${\displaystyle Z(s)}$ the subject of the expression results in,

${\displaystyle Z(s)=\left({\frac {R(s)}{Z(k)}}+{\frac {k}{sZ(k)}}\right)^{-1}+\left({\frac {1}{Z(k)R(s)}}+{\frac {s}{kZ(k)}}\right)^{-1}}$

An example of one cycle of Bott-Duffin synthesis is shown in the figures. The four terms in this expression are, respectively, a PRF (${\displaystyle Z_{2}(s)}$ in the diagram), an inductance, ${\displaystyle L}$, in parallel with it, another PRF (${\displaystyle Z_{1}(s)}$ in the diagram), and a capacitance, ${\displaystyle C}$, in parallel with it. A pair of critical frequencies on the ${\displaystyle i\omega }$ axis is then extracted from each of the two new PRFs (details not given here) each realised as a resonant circuit. The two residual PRFs (${\displaystyle Y_{3}(s)}$ and ${\displaystyle Z_{4}(s)}$ in the diagram) are each two degrees lower than ${\displaystyle Z(s)}$. The same procedure is then repeatedly applied to the new PRFs generated until just a single element remains. Since the number of PRFs generated doubles with each cycle, the number of elements synthesised will grow exponentially. Although the Bott-Duffin method avoids the use of transformers and can be applied to any expression capable of realisation as a passive network, it has limited practical use due to the high component count required.

Bayard synthesis

Bayard synthesis is a state-space synthesis method based on the Gauss factorisation procedure. This method returns a synthesis using the minimum number of resistors and contains no gyrators. However, the method is non-canonical and will, in general, return a non-minimal number of reactance elements.

Darlington synthesis

Darlington synthesis starts from a different perspective to the techniques discussed so far, which all start from a prescribed rational function and realise it as a one-port impedance. Darlington synthesis starts with a prescribed rational function that is the desired transfer function of a two-port network. Darlington showed that any PRF can be realised as a two-port network using only L and C elements with a single resistor terminating the output port. The Darlington and related methods are called the insertion loss method. The method can be extended to multi-port networks with each port terminated with a single resistor.

The Darlington method, in general, will require transformers or coupled inductors. However, most common filter types can be constructed by the Darlington method without these undesirable features.

Active and digital realisations

If the requirement to use only passive elements is lifted, then the realisation can be greatly simplified. Amplifiers can be used to buffer the parts of the network from each other so that they do not interact. Each buffered cell can directly realise a pair of poles of the rational function. There is then no need for any kind of iterative expansion of the function. The first example of this kind of synthesis is due to Stephen Butterworth in 1930. The Butterworth filter he produced became a classic of filter design, but more frequently implemented with purely passive rather than active components. More generally applicable designs of this kind include the Sallen–Key topology due to R. P. Sallen and E. L. Key in 1955 at MIT Lincoln Laboratory, and the biquadratic filter. Like the Darlington approach, Butterworth and Sallen-Key start with a prescribed transfer function rather than an impedance. A major practical advantage of active implementation is that it can avoid the use of wound components (transformers and inductors) altogether. These are undesirable for manufacturing reasons. Another feature of active designs is that they are not limited to PRFs.

Digital realisations, like active circuits, are not limited to PRFs and can implement any rational function simply by programming it in. However, the function may not be stable. That is, it may lead to oscillation. PRFs are guaranteed to be stable, but other functions may not be. The stability of a rational function can be determined by examining the poles and zeroes of the function and applying the Nyquist stability criterion.

References

1. Aatre, p. 259
2. E. Cauer et al., p. 4
3. Storer, p.3
4. Robertson et al., p. 107
5. Robertson et al., p. 108
6. Paarman, p. 15
7. Robertson et al., p. 107
8. Shenoi, pp. 4, 18
9. Paarman, pp. 15–16
10. Bakshi & Chitode, p. 6-1
11. Anderson & Vongpanitlerd, p. 509
12. Wanhammar, p. 10
13. Bakshi & Chitode, p. 6-1
14. E. Cauer et al., p.4
15. Hughes et al., p. 288
16. Hughes et al., p. 288
17. Bakshi & Chitode, p. 6-1
18. E. Cauer et al., pp. 3-4
19. Kalman, p. 4
20. E. Cauer et al., pp. 6-7
21. Kalman, p. 6
22. Kalman, p. 4
23. Hubbard, p. 3
24. Hubbard, p. 3
25. Wing, p. 122
26. Kalman, p. 7
27. Chen & Smith, p. 38
28. Chen & Smith, pp. 38, 50
29. • Wing, p. 128
    • Kalman, p. 10
30. E. Cauer et al., p. 7
31. Wing, p. 128
32. Belevitch, p. 854
33. Lee, pp. 756-757
34. Kalman, p. 10
35. E. Cauer et al., p. 5
36. Swanson, p. 58
37. McCarthy, p. 51
38. Swanson, p. 58
39. Darlington, p. 7
40. Chen & Hu, p. 8
41. Chen & Smith, p. 35
42. Hughes et al., p. 286
43. Hughes et al., pp. 287–288
44. Awang, p. 227
45. Matthaei et al., pp. 3-5
46. Matthaei et al., p. 681
47. Matthaei et al., p. 5
48. Matthaei et al., pp. 121
49. Wanhammar, p. 58
50. Chen & Smith, p. 35
51. Chen & Hu, p. 8
52. Bakshi & Bakshi, p. 3-13–3-14
53. Wing, p. 115
54. • Bakshi & Bakshi, p. 3-23, 3-30–3-31, 3-37
    • Wing, p. 115
55. Bakshi & Bakshi, pp. 3-23–3-24
56. Wing, pp. 115-116
57. Wing, pp. 115-116
58. Bakshi & Bakshi, pp. 3-31, 3-33
59. Bakshi & Bakshi, pp. 3-30–3-31, 3-37
60. Ghosh & Chakroborty, p. 771
61. Bakshi & Bakshi, pp. 3-28–3-29
62. Bakshi & Bakshi, p. 3-21
63. Bakshi & Bakshi, p. 3-29
64. Bakshi & Bakshi, p. 3-21
65. Houpis & Lubelfeld, p. 183
66. Bakshi & Bakshi, p. 3-30
67. Wing, p. 115
68. Hughes et al., p. 283
69. Carlin & Civalleri, p. 254
70. • Wing, pp. 115-116
    • Ghosh & Chakroborty, pp. 792-793
71. Wing, pp. 117-118
72. Wing, p. 122
73. • Wing, p. 116
    • Ghosh & Chakroborty, p. 793
74. Wing, pp. 116-117
75. Wing, p. 117
76. Wing, p. 119
77. Wing, p. 117
78. Wing, p. 117
79. Wing, p. 117
80. Wing, pp. 117-118
81. Wing, pp. 117, 120
82. Wing, p. 121
83. Wing, p. 122
84. Hughes et al., p. 284
85. Hughes et al., pp. 284–285
86. • Wing, pp. 122–126
    • Youla, pp. 65–66
87. Kalman, p. 7
88. Anderson & Vongpanitlerd, p. 427
89. E. Cauer et al., p. 7
90. Sisodia, p. 5.13
91. Belevitch, p. 853
92. Wing, p. 164
93. Belevitch, p. 852
94. Belevitch, p. 850
95. Glisson, p. 727
96. Vaisband et al., p. 280
97. Comer & Comer, p. 435
98. Wing, p. 91
99. Chao & Athans, p. 524

Bibliography

Sources

• Aatre, Vasudev K., Network Theory and Filter Design, New Age International, 1986 ISBN 0852260148.
• Anderson, Brian D.O.; Vongpanitlerd, Sumeth, Network Analysis and Synthesis: A Modern Systems Theory Approach, Courier Corporation, 2013 ISBN 0486152170.
• Awang, Zaiki, Microwave Systems Design, Springer, 2013 ISBN 9789814451246.
• Bakshi, U.A.; Bakshi, A.V., Circuit Analysis - II, Technical Publications, 2009 ISBN 9788184315974.
• Bakshi, U.A.; Chitode, J.S., Linear Systems Analysis, Technical Publications, 2009 ISBN 8184317409.
• Belevitch, Vitold, "Summary of the history of circuit theory", Proceedings of the IRE, vol. 50, iss. 5, pp. 848–855, May 1962.
• Carlin, Herbert J.; Civalleri, Pier Paolo, Wideband Circuit Design, CRC Press, 1997 ISBN 9780849378973.
• Cauer, Emil; Mathis, Wolfgang; Pauli, Rainer, "Life and Work of Wilhelm Cauer (1900 – 1945)", Proceedings of the Fourteenth International Symposium of Mathematical Theory of Networks and Systems (MTNS2000), Perpignan, June, 2000.
• Chao, Alan; Athans, Michael, "Stability robustness to unstructured uncertainty for linear time invariant systems", ch. 30 in, Levine, William S., The Control Handbook, CRC Press, 1996 ISBN 0849385709.
• Chen, Michael Z.Q.; Hu, Yinlong, Inerter and Its Application in Vibration Control Systems, Springer, 2019 ISBN 981107089X.
• Chen, Michael Z.Q.; Smith, Malcolm C., "Electrical and mechanical passive network synthesis", pp. 35–50 in, Blondel, Vincent D.; Boyd, Stephen P.; Kimuru, Hidenori (eds), Recent Advances in Learning and Control, Springer, 2008 ISBN 9781848001541.
• Comer, David J.; Comer, Donald T., Advanced Electronic Circuit Design, Wiley, 2003 ISBN 0471228281.
• Darlington, Sidney "A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors", IEEE Transactions: Circuits and Systems, vol. 31, pp. 3–13, 1984.
• Ghosh, S.P., Chakroborty, A.K., Network Analysis and Synthesis, Tata McGraw Hill, 2010 ISBN 9781259081422.
• Glisson, Tildon H., Introduction to Circuit Analysis and Design, Springer, 2011 ISBN ISBN 9048194431.
• Houpis, Constantine H.; Lubelfeld, Jerzy, Pulse Circuits, Simon and Schuster, 1970 OCLC 637996615.
• Hubbard, John H., "The Bott-Duffin synthesis of electrical circuits", pp. 33–40 in, Kotiuga, P. Robert (ed), A Celebration of the Mathematical Legacy of Raoul Bott, American Mathematical Society, 2010 ISBN 9780821883815.
• Hughes, Timothy H.; Morelli, Alessandro; Smith, Malcolm C., "Electrical network synthesis: A survey of recent work", pp. 281–293 in, Tempo, R.; Yurkovich, S.; Misra, P. (eds), Emerging Applications of Control and Systems Theory, Springer, 2018 ISBN 9783319670676.
• Kalman, Rudolf, "Old and new directions of research in systems theory", pp. 3–13 in, Willems, Jan; Hara, Shinji; Ohta, Yoshito; Fujioka, Hisaya (eds), Perspectives in Mathematical System Theory, Control, and Signal Processing, Springer, 2010 ISBN 9783540939177.
• Lee, Thomas H., Planar Microwave Engineering, Cambridge University Press, 2004 ISBN 0521835267.
• Matthaei, George L.; Young, Leo; Jones, E.M.T., Microwave Filters, Impedance-Matching Networks, and Coupling Structures, McGraw-Hill 1964 LCCN 64-7937.
• Paarmann, Larry D., Design and Analysis of Analog Filters, Springer Science & Business Media, 2001 ISBN 0792373731.
• Robertson, Ean; Somjit, Nutapong; Chongcheawchamnan Mitchai, Microwave and Millimetre-Wave Design for Wireless Communications, John Wiley & Sons, 2016 ISBN 1118917219.
• Shenoi, Belle A., Magnitude and Delay Approximation of 1-D and 2-D Digital Filters, Springer, 2012 ISBN 3642585736.
• Sisodia, M.L.; Gupta, Vijay Laxmi, Microwaves : Introduction To Circuits, Devices And Antennas, New Age International, 2007 ISBN 8122413382.
• Storer, James Edward, Passive Network Synthesis, McGraw-Hill, 1957 OCLC 435995425.
• Swanson, David C., Signal Processing for Intelligent Sensor Systems with MATLAB, CRC Press, 2012 ISBN 1420043056.
• Vaisband, Inna P.; Jakushokas, Renatas, Popovich, Mikhail; Mezhiba, Andrey V.; Köse, Selçuk; Friedman Eby G., On-Chip Power Delivery and Management, Springer, 2016 ISBN 3319293958.
• Wanhammar, Lars, Analog Filters using MATLAB, Springer, 2009 ISBN 0387927670.
• Youla, Dante C., Theory and Synthesis of Linear Passive Time-Invariant Networks, Cambridge University Press, 2015 ISBN 1107122864.
• Wing, Omar, Classical Circuit Theory, Springer, 2008 ISBN 0387097406.

Primary documents

• Bott, Raoul; Duffin, Richard, "Impedance synthesis without use of transformers", Journal of Applied Physics, vol. 20, iss. 8, p. 816, August 1949.
• Bode, Hendrik, Network Analysis and Feedback Amplifier Design, pp. 360–371, D. Van Nostrand Company, 1945 OCLC 1078811368.
• Brune, Otto, "Synthesis of a finite two-terminal network whose driving-point impedance is a prescribed function of frequency", MIT Journal of Mathematics and Physics, vol. 10, pp. 191–236, April 1931.
• Butterworth, Stephen, "On the theory of filter amplifiers", Experimental Wireless and the Wireless Engineer, vol. 7, no. 85, pp. 536–541, October 1930.
• Cauer, Wilhelm, "Die Verwirklichung der Wechselstromwiderstände vorgeschriebener Frequenzabhängigkeit" (The realisation of impedances of prescribed frequency dependence), Archiv für Elektrotechnik, vol. 17, pp. 355–388, 1926 (in German).
• Cauer, Wilhelm, "Vierpole mit vorgeschriebenem D ̈ampfungs-verhalten", Telegraphen-, Fernsprech-, Funk- und Fern-sehtechnik, vol. 29, pp. 185–192, 228–235. 1940 (in German).
• Cocci, Giovanni, "Rappresentazione di bipoli qualsiasi con quadripoli di pure reattanze chiusi su resistenze", Alta Frequenza, vol. 9, pp. 685–698, 1940 (in Italian).
• Darlington, Sidney, "Synthesis of reactance 4-poles which produce prescribed insertion loss characteristics: Including special applications to filter design", MIT Journal of Mathematics and Physics, vol. 18, pp. 257–353, April 1939.
• Fano, Robert, "Theoretical limitations on the broadband matching of arbitrary impedances", Journal of the Franklin Institute, vol. 249, iss. 1, pp. 57–83, January 1950.
• Fialko, Aaron; Gerst, Irving, "Impedance synthesis without mutual coupling", Quarterly of Applied Mathematics, vol. 12, No. 4, pp. 420–422, 1955
• Hughes, Timothy H., "Why RLC realizations of certain impedances need many more energy storage elements than expected", IEEE Transactions on Automatic Control, vol. 62, iss 9, pp. 4333-4346, September 2017.
• Hughes, Timothy H., "Passivity and electric circuits: a behavioral approach", IFAC-PapersOnLine, vol. 50, iss. 1, pp. 15500–15505, July 2017.
• Ladenheim, Edward L., A Synthesis of Biquadratic Impedances, Master's thesis, Polytechnic Institute of Brooklyn, New York, 1948.
• Pantell, R.H., "A new method of driving point impedance synthesis", Proceedings of the IRE, vol. 42, iss. 5, p. 861, 1954.
• Reza, F.M., "A bridge equivalent for a Brune cycle terminated in a resistor", Proceedings of the IRE, vol. 42, iss. 8, p. 1321, 1954.
• Richards, Paul I., "A special class of functions with positive real part in a half-plane", Duke Mathematical Journal, vol. 14, no. 3, 777–786, 1947.
• Sallen, R.P.; Key, E.L, "A practical method of designing RC active filters", IRE Transactions on Circuit Theory, vol. 2, iss. 1 pp. 74–85, March 1955.
• Smith, Malcolm C., "Synthesis of mechanical networks: the inerter", IEEE Transactions on Automatic Control, vol. 47, iss. 10, pp. 1648–1662, Oct 2002.
• Storer, J.E., "Relationship between the Bott-Duffin and Pantell impedance synthesis", Proceedings of the IRE, vol. 42, iss. 9, p. 1451, September 1954.

• Network synthesis
• Analog circuits
• Electronic design
• History of electronic engineering