Misplaced Pages

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Focal length" – news · newspapers · books · scholar · JSTOR (November 2021) (Learn how and when to remove this message)

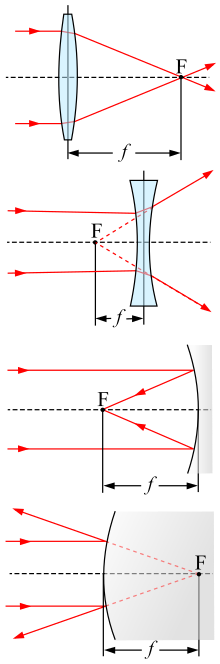
The focal length of an optical system is a measure of how strongly the system converges or diverges light; it is the inverse of the system's optical power. A positive focal length indicates that a system converges light, while a negative focal length indicates that the system diverges light. A system with a shorter focal length bends the rays more sharply, bringing them to a focus in a shorter distance or diverging them more quickly. For the special case of a thin lens in air, a positive focal length is the distance over which initially collimated (parallel) rays are brought to a focus, or alternatively a negative focal length indicates how far in front of the lens a point source must be located to form a collimated beam. For more general optical systems, the focal length has no intuitive meaning; it is simply the inverse of the system's optical power.

In most photography and all telescopy, where the subject is essentially infinitely far away, longer focal length (lower optical power) leads to higher magnification and a narrower angle of view; conversely, shorter focal length or higher optical power is associated with lower magnification and a wider angle of view. On the other hand, in applications such as microscopy in which magnification is achieved by bringing the object close to the lens, a shorter focal length (higher optical power) leads to higher magnification because the subject can be brought closer to the center of projection.

Thin lens approximation

For a thin lens in air, the focal length is the distance from the center of the lens to the principal foci (or focal points) of the lens. For a converging lens (for example a convex lens), the focal length is positive and is the distance at which a beam of collimated light will be focused to a single spot. For a diverging lens (for example a concave lens), the focal length is negative and is the distance to the point from which a collimated beam appears to be diverging after passing through the lens.

When a lens is used to form an image of some object, the distance from the object to the lens u, the distance from the lens to the image v, and the focal length f are related by

${\displaystyle {\frac {1}{f}}={\frac {1}{u}}+{\frac {1}{v}}\ .}$

The focal length of a thin convex lens can be easily measured by using it to form an image of a distant light source on a screen. The lens is moved until a sharp image is formed on the screen. In this case ⁠1/u⁠ is negligible, and the focal length is then given by

${\displaystyle f\approx v\ .}$

Determining the focal length of a concave lens is somewhat more difficult. The focal length of such a lens is defined as the point at which the spreading beams of light meet when they are extended backwards. No image is formed during such a test, and the focal length must be determined by passing light (for example, the light of a laser beam) through the lens, examining how much that light becomes dispersed/ bent, and following the beam of light backwards to the lens's focal point.

General optical systems

For a thick lens (one which has a non-negligible thickness), or an imaging system consisting of several lenses or mirrors (e.g. a photographic lens or a telescope), there are several related concepts that are referred to as focal lengths:

Effective focal length (EFL)

The effective focal length is the inverse of the optical power of an optical system, and is the value used to calculate the magnification of the system. The imaging properties of the optical system can be modeled by replacing the system with an ideal thin lens with the same EFL. The EFL also provides a simple method for finding the nodal points without tracing any rays. It was previously called equivalent focal length (not to be confused with 35 mm-equivalent focal length).

Front focal length (FFL)

The front focal length f is the distance from the front focal point F to the front principal plane H.

Rear focal length (RFL)

The rear focal length f′ is the distance from the rear principal plane H′ to the rear focal point F′.

Front focal distance (FFD)

The front focal distance (FFD) (s_F) is the distance from the front focal point of the system (F) to the vertex of the first optical surface (S₁). Some authors refer to this as "front focal length".

Back focal distance (BFD)

Back focal distance (BFD) (s′_F′) is the distance from the vertex of the last optical surface of the system (S₂) to the rear focal point (F′). Some authors refer to this as "back focal length".

For an optical system in air the effective focal length, front focal length, and rear focal length are all the same and may be called simply "focal length".

For an optical system in a medium other than air or vacuum, the front and rear focal lengths are equal to the EFL times the refractive index of the medium in front of or behind the lens (n₁ and n₂ in the diagram above). The term "focal length" by itself is ambiguous in this case. The historical usage was to define the "focal length" as the EFL times the index of refraction of the medium. For a system with different media on both sides, such as the human eye, the front and rear focal lengths are not equal to one another, and convention may dictate which one is called "the focal length" of the system. Some modern authors avoid this ambiguity by instead defining "focal length" to be a synonym for EFL.

The distinction between front/rear focal length and EFL is important for studying the human eye. The eye can be represented by an equivalent thin lens at an air/fluid boundary with front and rear focal lengths equal to those of the eye, or it can be represented by a different equivalent thin lens that is totally in air, with focal length equal to the eye's EFL.

For the case of a lens of thickness d in air (n₁ = n₂ = 1), and surfaces with radii of curvature R₁ and R₂, the effective focal length f is given by the Lensmaker's equation:

$${\displaystyle {\frac {1}{f}}=(n-1)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}+{\frac {(n-1)d}{nR_{1}R_{2}}}\right),}$$where n is the refractive index of the lens medium. The quantity ⁠1/f⁠ is also known as the optical power of the lens.

The corresponding front focal distance is:$${\displaystyle {\mbox{FFD}}=f\left(1+{\frac {(n-1)d}{nR_{2}}}\right),}$$ and the back focal distance: $${\displaystyle {\mbox{BFD}}=f\left(1-{\frac {(n-1)d}{nR_{1}}}\right).}$$

In the sign convention used here, the value of R₁ will be positive if the first lens surface is convex, and negative if it is concave. The value of R₂ is negative if the second surface is convex, and positive if concave. Sign conventions vary between different authors, which results in different forms of these equations depending on the convention used.

For a spherically-curved mirror in air, the magnitude of the focal length is equal to the radius of curvature of the mirror divided by two. The focal length is positive for a concave mirror, and negative for a convex mirror. In the sign convention used in optical design, a concave mirror has negative radius of curvature, so

$${\displaystyle f=-{R \over 2},}$$

where R is the radius of curvature of the mirror's surface.

See Radius of curvature (optics) for more information on the sign convention for radius of curvature used here.

In photography

Camera lens focal lengths are usually specified in millimetres (mm), but some older lenses are marked in centimetres (cm) or inches.

Focal length (f) and field of view (FOV) of a lens are inversely proportional. For a standard rectilinear lens, ${\textstyle \mathrm {FOV} =2\arctan {\left({x \over 2f}\right)}}$, where x is the width of the film or imaging sensor.

When a photographic lens is set to "infinity", its rear principal plane is separated from the sensor or film, which is then situated at the focal plane, by the lens's focal length. Objects far away from the camera then produce sharp images on the sensor or film, which is also at the image plane.

To render closer objects in sharp focus, the lens must be adjusted to increase the distance between the rear principal plane and the film, to put the film at the image plane. The focal length f, the distance from the front principal plane to the object to photograph s₁, and the distance from the rear principal plane to the image plane s₂ are then related by:

$${\displaystyle {\frac {1}{s_{1}}}+{\frac {1}{s_{2}}}={\frac {1}{f}}\,.}$$

As s₁ is decreased, s₂ must be increased. For example, consider a normal lens for a 35 mm camera with a focal length of f = 50 mm. To focus a distant object (s₁ ≈ ∞), the rear principal plane of the lens must be located a distance s₂ = 50 mm from the film plane, so that it is at the location of the image plane. To focus an object 1 m away (s₁ = 1,000 mm), the lens must be moved 2.6 mm farther away from the film plane, to s₂ = 52.6 mm.

The focal length of a lens determines the magnification at which it images distant objects. It is equal to the distance between the image plane and a pinhole that images distant objects the same size as the lens in question. For rectilinear lenses (that is, with no image distortion), the imaging of distant objects is well modelled as a pinhole camera model. This model leads to the simple geometric model that photographers use for computing the angle of view of a camera; in this case, the angle of view depends only on the ratio of focal length to film size. In general, the angle of view depends also on the distortion.

A lens with a focal length about equal to the diagonal size of the film or sensor format is known as a normal lens; its angle of view is similar to the angle subtended by a large-enough print viewed at a typical viewing distance of the print diagonal, which therefore yields a normal perspective when viewing the print; this angle of view is about 53 degrees diagonally. For full-frame 35 mm-format cameras, the diagonal is 43 mm and a typical "normal" lens has a 50 mm focal length. A lens with a focal length shorter than normal is often referred to as a wide-angle lens (typically 35 mm and less, for 35 mm-format cameras), while a lens significantly longer than normal may be referred to as a telephoto lens (typically 85 mm and more, for 35 mm-format cameras). Technically, long focal length lenses are only "telephoto" if the focal length is longer than the physical length of the lens, but the term is often used to describe any long focal length lens.

Due to the popularity of the 35 mm standard, camera–lens combinations are often described in terms of their 35 mm-equivalent focal length, that is, the focal length of a lens that would have the same angle of view, or field of view, if used on a full-frame 35 mm camera. Use of a 35 mm-equivalent focal length is particularly common with digital cameras, which often use sensors smaller than 35 mm film, and so require correspondingly shorter focal lengths to achieve a given angle of view, by a factor known as the crop factor.

Optical power

The optical power of a lens or curved mirror is a physical quantity equal to the reciprocal of the focal length, expressed in metres. A dioptre is its unit of measurement with dimension of reciprocal length, equivalent to one reciprocal metre, 1 dioptre = 1 m. For example, a 2-dioptre lens brings parallel rays of light to focus at 1⁄2 metre. A flat window has an optical power of zero dioptres, as it does not cause light to converge or diverge.

The main benefit of using optical power rather than focal length is that the thin lens formula has the object distance, image distance, and focal length all as reciprocals. Additionally, when relatively thin lenses are placed close together their powers approximately add. Thus, a thin 2.0-dioptre lens placed close to a thin 0.5-dioptre lens yields almost the same focal length as a single 2.5-dioptre lens.

See also

• Depth of field
• Dioptre
• f-number or focal ratio

References

1. ^ Grievenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Press. pp. 6–9. ISBN 978-0-8194-5294-8.
2. ^ Simpson, Michael J. (24 February 2023). "Focal Length, EFL, and the Eye". Applied Optics. 62 (7): 1853–1857. Bibcode:2023ApOpt..62.1853S. doi:10.1364/AO.481805. PMID 37132938.
3. ^ Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. p. 168. ISBN 978-0805385663.
4. Simpson, Michael J. (28 March 2022). "Nodal points and the eye". Applied Optics. 61 (10): 2797–2804. Bibcode:2022ApOpt..61.2797S. doi:10.1364/AO.455464. PMID 35471355.
5. Hecht, Eugene (2017). "6.1 thick Lenses and Lens systems". Optics (5th ed.). Pearson. p. 257. ISBN 978-1-292-09693-3.
6. Hecht, Eugene (2002). Optics (4th ed.). Addison Wesley. pp. 244–245. ISBN 978-0805385663.
7. Charles, Jeffrey (2000). Practical astrophotography. Springer. pp. 63–66. ISBN 978-1-85233-023-1.
8. Stroebel, Leslie; Zakia, Richard D. (1993). The Focal encyclopedia of photography (3rd ed.). Focal Press. p. 27. ISBN 978-0-240-51417-8.
9. Stroebel, Leslie D. (1999). View Camera Technique. Focal Press. pp. 135–138. ISBN 978-0-240-80345-6.
10. Greivenkamp, John E. (2004). Field Guide to Geometrical Optics. SPIE Field Guides vol. FG01. SPIE. p. 7. ISBN 0-8194-5294-7.

• Geometrical optics
• Length
• Science of photography
• Optical quantities