Misplaced Pages

Functional encryption

General
Designers	Amit Sahai, Brent Waters, Dan Boneh, Shafi Goldwasser, Yael Kalai
Derived from	Public-key encryption
Related to	Homomorphic encryption

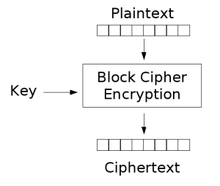
Functional encryption (FE) is a generalization of public-key encryption in which possessing a secret key allows one to learn a function of what the ciphertext is encrypting.

Formal definition

More precisely, a functional encryption scheme for a given functionality ${\displaystyle f}$ consists of the following four algorithms:

• ${\displaystyle ({\text{pk}},{\text{msk}})\leftarrow {\textsf {Setup}}(1^{\lambda })}$: creates a public key ${\displaystyle {\text{pk}}}$ and a master secret key ${\displaystyle {\text{msk}}}$.
• ${\displaystyle {\text{sk}}\leftarrow {\textsf {Keygen}}({\text{msk}},f)}$: uses the master secret key to generate a new secret key ${\displaystyle {\text{sk}}}$ for the function ${\displaystyle f}$.
• ${\displaystyle c\leftarrow {\textsf {Enc}}({\text{pk}},x)}$: uses the public key to encrypt a message ${\displaystyle x}$.
• ${\displaystyle y\leftarrow {\textsf {Dec}}({\text{sk}},c)}$: uses secret key to calculate ${\displaystyle y=f(x)}$ where ${\displaystyle x}$ is the value that ${\displaystyle c}$ encrypts.

The security of FE requires that any information an adversary learns from an encryption of ${\displaystyle x}$ is revealed by ${\displaystyle f(x)}$. Formally, this is defined by simulation.

Applications

Functional encryption generalizes several existing primitives including Identity-based encryption (IBE) and attribute-based encryption (ABE). In the IBE case, define ${\displaystyle F(k,x)}$ to be equal to ${\displaystyle x}$ when ${\displaystyle k}$ corresponds to an identity that is allowed to decrypt, and ${\displaystyle \perp }$ otherwise. Similarly, in the ABE case, define ${\displaystyle F(k,x)=x}$ when ${\displaystyle k}$ encodes attributes with permission to decrypt and ${\displaystyle \perp }$ otherwise.

History

Functional encryption was proposed by Amit Sahai and Brent Waters in 2005 and formalized by Dan Boneh, Amit Sahai and Brent Waters in 2010. Until recently, however, most instantiations of Functional Encryption supported only limited function classes such as boolean formulae. In 2012, several researchers developed Functional Encryption schemes that support arbitrary functions.

References

1. ^ Goldwasser, Shafi; Kalai, Yael; Ada Popa, Raluca; Vaikuntanathan, Vinod; Zeldovich, Nickolai (2013). Reusable garbled circuits and succinct functional encryption - Stoc 13 Proceedings of the 2013 ACM Symposium on Theory of Computing. New York, NY, USA: ACM. pp. 555–564. ISBN 978-1-4503-2029-0.
2. Amit Sahai; Brent Waters (2005). "Fuzzy Identity-Based Encryption". In Ronald Cramer (ed.). Advances in Cryptology. EUROCRYPT 2005: 24th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Proceedings. Springer. pp. 457–473. ISBN 978-3-540-25910-7. LCCN 2005926095.
3. Boneh, Dan; Amit Sahai; Brent Waters (2011). "Functional Encryption: Definitions and Challenges" (PDF). Proceedings of Theory of Cryptography Conference (TCC) 2011.
4. Gorbunov, Sergey; Hoeteck Wee; Vinod Vaikuntanathan (2013). "Attribute-Based Encryption for Circuits". Proceedings of STOC.
5. Sahai, Amit; Brent Waters (2012). "Attribute-Based Encryption for Circuits from Multilinear Maps" (PDF). arXiv:1210.5287.
6. Goldwasser, Shafi; Yael Kalai; Raluca Ada Popa; Vinod Vaikuntanathan; Nickolai Zeldovich (2013). "How to Run Turing Machines on Encrypted Data" (PDF). Advances in Cryptology – CRYPTO 2013. Lecture Notes in Computer Science. Vol. 8043. pp. 536–553. doi:10.1007/978-3-642-40084-1_30. hdl:1721.1/91472. ISBN 978-3-642-40083-4.

• Cryptographic primitives