Misplaced Pages

Microarray analysis techniques

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Gene chip analysis)
Example of an approximately 40,000 probe spotted oligo microarray with enlarged inset to show detail.

Microarray analysis techniques are used in interpreting the data generated from experiments on DNA (Gene chip analysis), RNA, and protein microarrays, which allow researchers to investigate the expression state of a large number of genes – in many cases, an organism's entire genome – in a single experiment. Such experiments can generate very large amounts of data, allowing researchers to assess the overall state of a cell or organism. Data in such large quantities is difficult – if not impossible – to analyze without the help of computer programs.

Introduction

Microarray data analysis is the final step in reading and processing data produced by a microarray chip. Samples undergo various processes including purification and scanning using the microchip, which then produces a large amount of data that requires processing via computer software. It involves several distinct steps, as outlined in the image below. Changing any one of the steps will change the outcome of the analysis, so the MAQC Project was created to identify a set of standard strategies. Companies exist that use the MAQC protocols to perform a complete analysis.

The steps required in a microarray experiment

Techniques

National Center for Toxicological Research scientist reviews microarray data

Most microarray manufacturers, such as Affymetrix and Agilent, provide commercial data analysis software alongside their microarray products. There are also open source options that utilize a variety of methods for analyzing microarray data.

Aggregation and normalization

Comparing two different arrays or two different samples hybridized to the same array generally involves making adjustments for systematic errors introduced by differences in procedures and dye intensity effects. Dye normalization for two color arrays is often achieved by local regression. LIMMA provides a set of tools for background correction and scaling, as well as an option to average on-slide duplicate spots. A common method for evaluating how well normalized an array is, is to plot an MA plot of the data. MA plots can be produced using programs and languages such as R and MATLAB.

Raw Affy data contains about twenty probes for the same RNA target. Half of these are "mismatch spots", which do not precisely match the target sequence. These can theoretically measure the amount of nonspecific binding for a given target. Robust Multi-array Average (RMA) is a normalization approach that does not take advantage of these mismatch spots but still must summarize the perfect matches through median polish. The median polish algorithm, although robust, behaves differently depending on the number of samples analyzed. Quantile normalization, also part of RMA, is one sensible approach to normalize a batch of arrays in order to make further comparisons meaningful.

The current Affymetrix MAS5 algorithm, which uses both perfect match and mismatch probes, continues to enjoy popularity and do well in head to head tests.

Flowchart showing how the MAS5 algorithm by Agilent works.

Factor analysis for Robust Microarray Summarization (FARMS) is a model-based technique for summarizing array data at perfect match probe level. It is based on a factor analysis model for which a Bayesian maximum a posteriori method optimizes the model parameters under the assumption of Gaussian measurement noise. According to the Affycomp benchmark FARMS outperformed all other summarizations methods with respect to sensitivity and specificity.

Identification of significant differential expression

Many strategies exist to identify array probes that show an unusual level of over-expression or under-expression. The simplest one is to call "significant" any probe that differs by an average of at least twofold between treatment groups. More sophisticated approaches are often related to t-tests or other mechanisms that take both effect size and variability into account. Curiously, the p-values associated with particular genes do not reproduce well between replicate experiments, and lists generated by straight fold change perform much better. This represents an extremely important observation, since the point of performing experiments has to do with predicting general behavior. The MAQC group recommends using a fold change assessment plus a non-stringent p-value cutoff, further pointing out that changes in the background correction and scaling process have only a minimal impact on the rank order of fold change differences, but a substantial impact on p-values.

Clustering

Clustering is a data mining technique used to group genes having similar expression patterns. Hierarchical clustering, and k-means clustering are widely used techniques in microarray analysis.

Hierarchical clustering

Main article: Hierarchical clustering

Hierarchical clustering is a statistical method for finding relatively homogeneous clusters. Hierarchical clustering consists of two separate phases. Initially, a distance matrix containing all the pairwise distances between the genes is calculated. Pearson's correlation and Spearman's correlation are often used as dissimilarity estimates, but other methods, like Manhattan distance or Euclidean distance, can also be applied. Given the number of distance measures available and their influence in the clustering algorithm results, several studies have compared and evaluated different distance measures for the clustering of microarray data, considering their intrinsic properties and robustness to noise. After calculation of the initial distance matrix, the hierarchical clustering algorithm either (A) joins iteratively the two closest clusters starting from single data points (agglomerative, bottom-up approach, which is fairly more commonly used), or (B) partitions clusters iteratively starting from the complete set (divisive, top-down approach). After each step, a new distance matrix between the newly formed clusters and the other clusters is recalculated. Hierarchical cluster analysis methods include:

  • Single linkage (minimum method, nearest neighbor)
  • Average linkage (UPGMA)
  • Complete linkage (maximum method, furthest neighbor)

Different studies have already shown empirically that the Single linkage clustering algorithm produces poor results when employed to gene expression microarray data and thus should be avoided.

K-means clustering

Main article: k-means clustering

K-means clustering is an algorithm for grouping genes or samples based on pattern into K groups. Grouping is done by minimizing the sum of the squares of distances between the data and the corresponding cluster centroid. Thus the purpose of K-means clustering is to classify data based on similar expression. K-means clustering algorithm and some of its variants (including k-medoids) have been shown to produce good results for gene expression data (at least better than hierarchical clustering methods). Empirical comparisons of k-means, k-medoids, hierarchical methods and, different distance measures can be found in the literature.

Pattern recognition

Commercial systems for gene network analysis such as Ingenuity and Pathway studio create visual representations of differentially expressed genes based on current scientific literature. Non-commercial tools such as FunRich, GenMAPP and Moksiskaan also aid in organizing and visualizing gene network data procured from one or several microarray experiments. A wide variety of microarray analysis tools are available through Bioconductor written in the R programming language. The frequently cited SAM module and other microarray tools are available through Stanford University. Another set is available from Harvard and MIT.

Example of FunRich tool output. Image shows the result of comparing 4 different genes.

Specialized software tools for statistical analysis to determine the extent of over- or under-expression of a gene in a microarray experiment relative to a reference state have also been developed to aid in identifying genes or gene sets associated with particular phenotypes. One such method of analysis, known as Gene Set Enrichment Analysis (GSEA), uses a Kolmogorov-Smirnov-style statistic to identify groups of genes that are regulated together. This third-party statistics package offers the user information on the genes or gene sets of interest, including links to entries in databases such as NCBI's GenBank and curated databases such as Biocarta and Gene Ontology. Protein complex enrichment analysis tool (COMPLEAT) provides similar enrichment analysis at the level of protein complexes. The tool can identify the dynamic protein complex regulation under different condition or time points. Related system, PAINT and SCOPE performs a statistical analysis on gene promoter regions, identifying over and under representation of previously identified transcription factor response elements. Another statistical analysis tool is Rank Sum Statistics for Gene Set Collections (RssGsc), which uses rank sum probability distribution functions to find gene sets that explain experimental data. A further approach is contextual meta-analysis, i.e. finding out how a gene cluster responds to a variety of experimental contexts. Genevestigator is a public tool to perform contextual meta-analysis across contexts such as anatomical parts, stages of development, and response to diseases, chemicals, stresses, and neoplasms.

Significance analysis of microarrays (SAM)

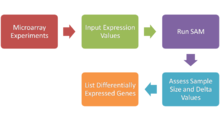
Significance analysis of microarrays (SAM) is a statistical technique, established in 2001 by Virginia Tusher, Robert Tibshirani and Gilbert Chu, for determining whether changes in gene expression are statistically significant. With the advent of DNA microarrays, it is now possible to measure the expression of thousands of genes in a single hybridization experiment. The data generated is considerable, and a method for sorting out what is significant and what isn't is essential. SAM is distributed by Stanford University in an R-package.

SAM identifies statistically significant genes by carrying out gene specific t-tests and computes a statistic dj for each gene j, which measures the strength of the relationship between gene expression and a response variable. This analysis uses non-parametric statistics, since the data may not follow a normal distribution. The response variable describes and groups the data based on experimental conditions. In this method, repeated permutations of the data are used to determine if the expression of any gene is significant related to the response. The use of permutation-based analysis accounts for correlations in genes and avoids parametric assumptions about the distribution of individual genes. This is an advantage over other techniques (e.g., ANOVA and Bonferroni), which assume equal variance and/or independence of genes.

Basic protocol

  • Perform microarray experiments — DNA microarray with oligo and cDNA primers, SNP arrays, protein arrays, etc.
  • Input Expression Analysis in Microsoft Excel — see below
  • Run SAM as a Microsoft Excel Add-Ins
  • Adjust the Delta tuning parameter to get a significant # of genes along with an acceptable false discovery rate (FDR)) and Assess Sample Size by calculating the mean difference in expression in the SAM Plot Controller
  • List Differentially Expressed Genes (Positively and Negatively Expressed Genes)

Running SAM

  • SAM is available for download online at http://www-stat.stanford.edu/~tibs/SAM/ for academic and non-academic users after completion of a registration step.
  • SAM is run as an Excel Add-In, and the SAM Plot Controller allows Customization of the False Discovery Rate and Delta, while the SAM Plot and SAM Output functionality generate a List of Significant Genes, Delta Table, and Assessment of Sample Sizes
  • Permutations are calculated based on the number of samples
  • Block Permutations
    • Blocks are batches of microarrays; for example for eight samples split into two groups (control and affected) there are 4!=24 permutations for each block and the total number of permutations is (24)(24)= 576. A minimum of 1000 permutations are recommended;

the number of permutations is set by the user when imputing correct values for the data set to run SAM

Response formats

Types:

  • Quantitative — real-valued (such as heart rate)
  • One class — tests whether the mean gene expression differs from zero
  • Two class — two sets of measurements
    • Unpaired — measurement units are different in the two groups; e.g. control and treatment groups with samples from different patients
    • Paired — same experimental units are measured in the two groups; e.g. samples before and after treatment from the same patients
  • Multiclass — more than two groups with each containing different experimental units; generalization of two class unpaired type
  • Survival — data of a time until an event (for example death or relapse)
  • Time course — each experimental units is measured at more than one time point; experimental units fall into a one or two class design
  • Pattern discovery — no explicit response parameter is specified; the user specifies eigengene (principal component) of the expression data and treats it as a quantitative response

Algorithm

SAM calculates a test statistic for relative difference in gene expression based on permutation analysis of expression data and calculates a false discovery rate. The principal calculations of the program are illustrated below.

The so constant is chosen to minimize the coefficient of variation of di. ri is equal to the expression levels (x) for gene i under y experimental conditions.

F a l s e   d i s c o v e r y   r a t e   ( F D R ) = M e d i a n   ( o r   90 t h   p e r c e n t i l e )   o f   #   o f   f a l s e l y   c a l l e d   g e n e s N u m b e r   o f   g e n e s   c a l l e d   s i g n i f i c a n t {\displaystyle \mathrm {False\ discovery\ rate\ (FDR)={\frac {Median\ (or\ 90^{th}\ percentile)\ of\ \#\ of\ falsely\ called\ genes}{Number\ of\ genes\ called\ significant}}} }

Fold changes (t) are specified to guarantee genes called significant change at least a pre-specified amount. This means that the absolute value of the average expression levels of a gene under each of two conditions must be greater than the fold change (t) to be called positive and less than the inverse of the fold change (t) to be called negative.

The SAM algorithm can be stated as:

  1. Order test statistics according to magnitude
  2. For each permutation compute the ordered null (unaffected) scores
  3. Plot the ordered test statistic against the expected null scores
  4. Call each gene significant if the absolute value of the test statistic for that gene minus the mean test statistic for that gene is greater than a stated threshold
  5. Estimate the false discovery rate based on expected versus observed values

Output

  • Significant gene sets
    • Positive gene set — higher expression of most genes in the gene set correlates with higher values of the phenotype y
    • Negative gene set — lower expression of most genes in the gene set correlates with higher values of the phenotype y

SAM features

  • Data from Oligo or cDNA arrays, SNP array, protein arrays, etc. can be utilized in SAM
  • Correlates expression data to clinical parameters
  • Correlates expression data with time
  • Uses data permutation to estimates False Discovery Rate for multiple testing
  • Reports local false discovery rate (the FDR for genes having a similar di as that gene) and miss rates
  • Can work with blocked design for when treatments are applied within different batches of arrays
  • Can adjust threshold determining number of gene called significant

Error correction and quality control

Quality control

Entire arrays may have obvious flaws detectable by visual inspection, pairwise comparisons to arrays in the same experimental group, or by analysis of RNA degradation. Results may improve by removing these arrays from the analysis entirely.

Background correction

Depending on the type of array, signal related to nonspecific binding of the fluorophore can be subtracted to achieve better results. One approach involves subtracting the average signal intensity of the area between spots. A variety of tools for background correction and further analysis are available from TIGR, Agilent (GeneSpring), and Ocimum Bio Solutions (Genowiz).

Spot filtering

Visual identification of local artifacts, such as printing or washing defects, may likewise suggest the removal of individual spots. This can take a substantial amount of time depending on the quality of array manufacture. In addition, some procedures call for the elimination of all spots with an expression value below a certain intensity threshold.

See also

References

  1. ^ Subramanian A, Tamayo P, Mootha VK, et al. (2005). "Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles". Proc. Natl. Acad. Sci. U.S.A. 102 (43): 15545–50. doi:10.1073/pnas.0506580102. PMC 1239896. PMID 16199517.
  2. Dr. Leming Shi, National Center for Toxicological Research. "MicroArray Quality Control (MAQC) Project". U.S. Food and Drug Administration. Retrieved 2007-12-26.
  3. "GenUs BioSystems - Services - Data Analysis". Retrieved 2008-01-02.
  4. "Agilent | DNA Microarrays". Archived from the original on December 22, 2007. Retrieved 2008-01-02.
  5. "LIMMA Library: Linear Models for Microarray Data". Retrieved 2008-01-01.
  6. Gatto, Laurent; Breckels, Lisa M.; Naake, Thomas; Gibb, Sebastian (2015). "Visualization of proteomics data using R and Bioconductor". Proteomics. 15 (8): 1375–1389. doi:10.1002/pmic.201400392. ISSN 1615-9853. PMC 4510819. PMID 25690415.
  7. "Create intensity versus ratio scatter plot of microarray data - MATLAB mairplot". MathWorks. Retrieved 2023-11-24.
  8. Irizarry, RA; Hobbs, B; Collin, F; Beazer-Barclay, YD; Antonellis, KJ; Scherf, U; Speed, TP (2003). "Exploration, normalization, and summaries of high density oligonucleotide array probe level data". Biostatistics. 4 (2): 249–64. doi:10.1093/biostatistics/4.2.249. PMID 12925520.
  9. Bolstad BM, Irizarry RA, Astrand M, Speed TP (2003). "A comparison of normalization methods for high density oligonucleotide array data based on variance and bias". Bioinformatics. 19 (2): 185–93. doi:10.1093/bioinformatics/19.2.185. PMID 12538238.
  10. Giorgi FM, Bolger AM, Lohse M, Usadel B (2010). "Algorithm-driven Artifacts in median polish summarization of Microarray data". BMC Bioinformatics. 11: 553. doi:10.1186/1471-2105-11-553. PMC 2998528. PMID 21070630.
  11. Lim WK, Wang K, Lefebvre C, Califano A (2007). "Comparative analysis of microarray normalization procedures: effects on reverse engineering gene networks". Bioinformatics. 23 (13): i282–8. doi:10.1093/bioinformatics/btm201. PMID 17646307.
  12. Hochreiter S, Clevert DA, Obermayer K (2006). "A new summarization method for affymetrix probe level data". Bioinformatics. 22 (8): 943–949. doi:10.1093/bioinformatics/btl033. PMID 16473874.
  13. "Affycomp III: A Benchmark for Affymetrix GeneChip Expression Measures".
  14. ^ Shi L, Reid LH, Jones WD, et al. (2006). "The MicroArray Quality Control (MAQC) project shows inter- and intraplatform reproducibility of gene expression measurements". Nat. Biotechnol. 24 (9): 1151–61. doi:10.1038/nbt1239. PMC 3272078. PMID 16964229.
  15. Guo L, Lobenhofer EK, Wang C, et al. (2006). "Rat toxicogenomic study reveals analytical consistency across microarray platforms". Nat. Biotechnol. 24 (9): 1162–9. doi:10.1038/nbt1238. PMID 17061323. S2CID 8192240.
  16. Gentleman, Robert; et al. (2005). Bioinformatics and computational biology solutions using R and Bioconductor. New York: Springer Science+Business Media. ISBN 978-0-387-29362-2.
  17. Jaskowiak, Pablo A.; Campello, Ricardo J.G.B.; Costa, Ivan G. (2013). "Proximity Measures for Clustering Gene Expression Microarray Data: A Validation Methodology and a Comparative Analysis". IEEE/ACM Transactions on Computational Biology and Bioinformatics. 10 (4): 845–857. doi:10.1109/TCBB.2013.9. PMID 24334380. S2CID 760277.
  18. ^ Jaskowiak, Pablo A; Campello, Ricardo JGB; Costa, Ivan G (2014). "On the selection of appropriate distances for gene expression data clustering". BMC Bioinformatics. 15 (Suppl 2): S2. doi:10.1186/1471-2105-15-S2-S2. PMC 4072854. PMID 24564555.
  19. ^ de Souto, Marcilio C. P.; Costa, Ivan G.; de Araujo, Daniel S. A.; Ludermir, Teresa B.; Schliep, Alexander (2008). "Clustering cancer gene expression data: a comparative study". BMC Bioinformatics. 9 (1): 497. doi:10.1186/1471-2105-9-497. PMC 2632677. PMID 19038021.
  20. "Home". biostat.ucsf.edu.
  21. "Ingenuity Systems". Retrieved 2007-12-31.
  22. "Ariadne Genomics: Pathway Studio". Archived from the original on 2007-12-30. Retrieved 2007-12-31.
  23. "FunRich: Functional Enrichment Analysis". Retrieved 2014-09-09.
  25. "Software - Broad". Retrieved 2007-12-31.
  26. "BioCarta - Charting Pathways of Life". Retrieved 2007-12-31.
  27. Vinayagam A, Hu Y, Kulkarni M, Roesel C, et al. (2013). "Protein Complex-Based Analysis Framework for High-Throughput Data Sets. 6, rs5 (2013)". Sci. Signal. 6 (r5): rs5. doi:10.1126/scisignal.2003629. PMC 3756668. PMID 23443684.
  28. "DBI Web". Archived from the original on 2007-07-05. Retrieved 2007-12-31.
  29. "SCOPE". Archived from the original on 2011-08-17. Retrieved 2007-12-31.
  30. "RssGsc". Retrieved 2008-10-15.
  31. "SAM: Significance Analysis of Microarrays". tibshirani.su.domains. Retrieved 2023-11-24.
  32. ^ Chu, G., Narasimhan, B, Tibshirani, R, Tusher, V. "SAM "Significance Analysis of Microarrays" Users Guide and technical document."
  33. ^ Zang, S.; Guo, R.; et al. (2007). "Integration of statistical inference methods and a novel control measure to improve sensitivity and specificity of data analysis in expression profiling studies". Journal of Biomedical Informatics. 40 (5): 552–560. doi:10.1016/j.jbi.2007.01.002. PMID 17317331.
  34. ^ <Zhang, S. (2007). "A comprehensive evaluation of SAM, the SAM R-package and a simple modification to improve its performance." BMC Bioinformatics 8: 230.
  35. ^ Tusher, V. G.; Tibshirani, R.; et al. (2001). "Significance analysis of microarrays applied to the ionizing radiation response" (PDF). Proceedings of the National Academy of Sciences. 98 (9): 5116–5121. Bibcode:2001PNAS...98.5116G. doi:10.1073/pnas.091062498. PMC 33173. PMID 11309499.
  36. Dinu, I. P.; JD; Mueller, T; Liu, Q; Adewale, AJ; Jhangri, GS; Einecke, G; Famulski, KS; Halloran, P; Yasui, Y. (2007). "Improving gene set analysis of microarray data by SAM-GS". BMC Bioinformatics. 8: 242. doi:10.1186/1471-2105-8-242. PMC 1931607. PMID 17612399.
  37. Jeffery, I. H.; DG; Culhane, AC. (2006). "Comparison and evaluation of methods for generating differentially expressed gene lists from microarray data". BMC Bioinformatics. 7: 359. doi:10.1186/1471-2105-7-359. PMC 1544358. PMID 16872483.
  38. Larsson, O. W. C; Timmons, JA. (2005). "Considerations when using the significance analysis of microarrays (SAM) algorithm". BMC Bioinformatics. 6: 129. doi:10.1186/1471-2105-6-129. PMC 1173086. PMID 15921534.
  39. Wilson CL, Miller CJ (2005). "Simpleaffy: a BioConductor package for Affymetrix Quality Control and data analysis". Bioinformatics. 21 (18): 3683–5. doi:10.1093/bioinformatics/bti605. PMID 16076888.
  40. "J. Craig Venter Institute -- Software". Retrieved 2008-01-01.
  41. "Agilent | GeneSpring GX". Retrieved 2008-01-02.
  42. "Ocimum Biosolutions | Genowiz". Archived from the original on 2009-11-24. Retrieved 2009-04-02.

External links

Categories: