Misplaced Pages

Generalized Petersen graph

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Family of cubic graphs formed from regular and star polygons
The Dürer graph G(6, 2).

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.

Definition and notation

In Watkins' notation, G(n, k) is a graph with vertex set

{ u 0 , u 1 , … , u n − 1 , v 0 , v 1 , … , v n − 1 } {\displaystyle \{u_{0},u_{1},\ldots ,u_{n-1},v_{0},v_{1},\ldots ,v_{n-1}\}}

and edge set

{ u i u i + 1 , u i v i , v i v i + k ∣ 0 ≤ i ≤ n − 1 } {\displaystyle \{u_{i}u_{i+1},u_{i}v_{i},v_{i}v_{i+k}\mid 0\leq i\leq n-1\}}

where subscripts are to be read modulo n and k < n/2. Some authors use the notation GPG(n, k). Coxeter's notation for the same graph would be {n} + {n/k}, a combination of the Schläfli symbols for the regular n-gon and star polygon from which the graph is formed. The Petersen graph itself is G(5, 2) or {5} + {5/2}.

Any generalized Petersen graph can also be constructed from a voltage graph with two vertices, two self-loops, and one other edge.

Examples

Among the generalized Petersen graphs are the n-prism G(n, 1), the Dürer graph G(6, 2), the Möbius-Kantor graph G(8, 3), the dodecahedron G(10, 2), the Desargues graph G(10, 3) and the Nauru graph G(12, 5).

Four generalized Petersen graphs – the 3-prism, the 5-prism, the Dürer graph, and G(7, 2) – are among the seven graphs that are cubic, 3-vertex-connected, and well-covered (meaning that all of their maximal independent sets have equal size).

Properties

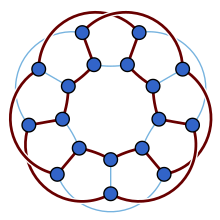
One of the three Hamiltonian cycles in G(9, 2). The other two Hamiltonian cycles in the same graph are symmetric under 40° rotations of the drawing.

This family of graphs possesses a number of interesting properties. For example:

  • G(n, k) is vertex-transitive (meaning that it has symmetries that take any vertex to any other vertex) if and only if (n, k) = (10, 2) or k ≡ ±1 (mod n).
  • G(n, k) is edge-transitive (having symmetries that take any edge to any other edge) only in the following seven cases: (n, k) = (4, 1), (5, 2), (8, 3), (10, 2), (10, 3), (12, 5), (24, 5). These seven graphs are therefore the only symmetric generalized Petersen graphs.
  • G(n, k) is bipartite if and only if n is even and k is odd.
  • G(n, k) is a Cayley graph if and only if k ≡ 1 (mod n).
  • G(n, k) is hypohamiltonian when n is congruent to 5 modulo 6 and k = 2, n − 2, or (n ± 1)/2 (these four choices of k lead to isomorphic graphs). It is also non-Hamiltonian when n is divisible by 4, at least equal to 8, and k = n/2. In all other cases it has a Hamiltonian cycle. When n is congruent to 3 modulo 6 G(n, 2) has exactly three Hamiltonian cycles. For G(n, 2), the number of Hamiltonian cycles can be computed by a formula that depends on the congruence class of n modulo 6 and involves the Fibonacci numbers.
  • Every generalized Petersen graph is a unit distance graph.

Isomorphisms

G(n, k) is isomorphic to G(n, l) if and only if k=l or kl ≡ ±1 (mod n).

Girth

The girth of G(n, k) is at least 3 and at most 8, in particular:

g ( G ( n , k ) ) ≤ min { 8 , k + 3 , n gcd ( n , k ) } . {\displaystyle g(G(n,k))\leq \min \left\{8,k+3,{\frac {n}{\gcd(n,k)}}\right\}.}

A table with exact girth values:

Condition Girth
n = 3 k {\displaystyle n=3k} 3
n = 4 k {\displaystyle n=4k} 4
k = 1 {\displaystyle k=1}
n = 5 k {\displaystyle n=5k} 5
n = 5 k / 2 {\displaystyle n=5k/2}
k = 2 {\displaystyle k=2}
n = 6 k {\displaystyle n=6k} 6
k = 3 {\displaystyle k=3}
n = 2 k + 2 {\displaystyle n=2k+2}
n = 7 k {\displaystyle n=7k} 7
n = 7 k / 2 {\displaystyle n=7k/2}
n = 7 k / 3 {\displaystyle n=7k/3}
k = 4 {\displaystyle k=4}
n = 2 k + 3 {\displaystyle n=2k+3}
n = 3 k ± 2 {\displaystyle n=3k\pm 2}
otherwise 8

Chromatic number and chromatic index

Generalized Petersen graphs are regular graphs of degree three, so according to Brooks' theorem their chromatic number can only be two or three. More exactly:

χ ( G ( n , k ) ) = { 2 2 ∣ n ∧ 2 ∤ k 3 2 ∤ n ∨ 2 ∣ k {\displaystyle \chi (G(n,k))={\begin{cases}2&2\mid n\land 2\nmid k\\3&2\nmid n\lor 2\mid k\\\end{cases}}}

Where ∧ {\displaystyle \land } denotes the logical AND, while ∨ {\displaystyle \lor } the logical OR. Here, ∣ {\displaystyle \mid } denotes divisibility, and ∤ {\displaystyle \nmid } denotes its negation. For example, the chromatic number of G ( 5 , 2 ) {\displaystyle G(5,2)} is 3.

  • A 3-coloring of the Petersen graph or '"`UNIQ--postMath-00000019-QINU`"' A 3-coloring of the Petersen graph or G ( 5 , 2 ) {\displaystyle G(5,2)}
  • A 2-coloring of the Desargues graph or '"`UNIQ--postMath-0000001A-QINU`"' A 2-coloring of the Desargues graph or G ( 10 , 3 ) {\displaystyle G(10,3)}
  • A 3-coloring of the Dürer graph or '"`UNIQ--postMath-0000001B-QINU`"' A 3-coloring of the Dürer graph or G ( 6 , 2 ) {\displaystyle G(6,2)}

The Petersen graph, being a snark, has a chromatic index of 4: its edges require four colors. All other generalized Petersen graphs have chromatic index 3. These are the only possibilities, by Vizing's theorem.

The generalized Petersen graph G(9, 2) is one of the few graphs known to have only one 3-edge-coloring.

  • A 4-edge-coloring of the Petersen graph or '"`UNIQ--postMath-0000001C-QINU`"' A 4-edge-coloring of the Petersen graph or G ( 5 , 2 ) {\displaystyle G(5,2)}
  • A 3-edge-coloring of the Dürer graph or '"`UNIQ--postMath-0000001D-QINU`"' A 3-edge-coloring of the Dürer graph or G ( 6 , 2 ) {\displaystyle G(6,2)}
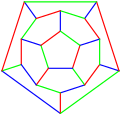  • A 3-edge-coloring of the dodecahedron or '"`UNIQ--postMath-0000001E-QINU`"' A 3-edge-coloring of the dodecahedron or G ( 10 , 2 ) {\displaystyle G(10,2)}
  • A 3-edge-coloring of the Desargues graph or '"`UNIQ--postMath-0000001F-QINU`"' A 3-edge-coloring of the Desargues graph or G ( 10 , 3 ) {\displaystyle G(10,3)}
  • A 3-edge-coloring of the Nauru graph or '"`UNIQ--postMath-00000020-QINU`"' A 3-edge-coloring of the Nauru graph or G ( 12 , 5 ) {\displaystyle G(12,5)}

The Petersen graph itself is the only generalized Petersen graph that is not 3-edge-colorable.

Perfect Colorings

All admissible matrices of all perfect 2-colorings of the graphs G(n, 2) and G(n, 3) are enumerated.

Admissible matrices
G(n, 2) G(n, 3)
[ 2 1 1 2 ] {\displaystyle {\begin{bmatrix}2&1\\1&2\end{bmatrix}}} All graphs All graphs
[ 2 1 2 1 ] {\displaystyle {\begin{bmatrix}2&1\\2&1\end{bmatrix}}} Just G(3m, 2) No graphs
[ 1 2 2 1 ] {\displaystyle {\begin{bmatrix}1&2\\2&1\end{bmatrix}}} No graphs Just G(2m,3)
[ 0 3 1 2 ] {\displaystyle {\begin{bmatrix}0&3\\1&2\end{bmatrix}}} No graphs Just G(4m,3)
[ 0 3 2 1 ] {\displaystyle {\begin{bmatrix}0&3\\2&1\end{bmatrix}}} Just G(5m,2) Just G(5m,3)
[ 0 3 3 0 ] {\displaystyle {\begin{bmatrix}0&3\\3&0\end{bmatrix}}} No graphs Just G(2m,3)

References

  1. Coxeter, H. S. M. (1950), "Self-dual configurations and regular graphs", Bulletin of the American Mathematical Society, 56 (5): 413–455, doi:10.1090/S0002-9904-1950-09407-5.
  2. Watkins, Mark E. (1969), "A Theorem on Tait Colorings with an Application to the Generalized Petersen Graphs", Journal of Combinatorial Theory, 6 (2): 152–164, doi:10.1016/S0021-9800(69)80116-X.
  3. Gross, Jonathan L.; Tucker, Thomas W. (1987), Topological Graph Theory, New York: Wiley. Example 2.1.2, p.58.
  4. Campbell, S. R.; Ellingham, M. N.; Royle, Gordon F. (1993), "A characterisation of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing, 13: 193–212, MR 1220613.
  5. Frucht, R.; Graver, J. E.; Watkins, M. E. (1971), "The groups of the generalized Petersen graphs", Proceedings of the Cambridge Philosophical Society, 70 (2): 211–218, doi:10.1017/S0305004100049811.
  6. Alspach, B. R. (1983), "The classification of Hamiltonian generalized Petersen graphs", Journal of Combinatorial Theory, Series B, 34 (3): 293–312, doi:10.1016/0095-8956(83)90042-4, MR 0714452.
  7. Thomason, Andrew (1982), "Cubic graphs with three Hamiltonian cycles are not always uniquely edge colorable", Journal of Graph Theory, 6 (2): 219–221, doi:10.1002/jgt.3190060218.
  8. Schwenk, Allen J. (1989), "Enumeration of Hamiltonian cycles in certain generalized Petersen graphs", Journal of Combinatorial Theory, Series B, 47 (1): 53–59, doi:10.1016/0095-8956(89)90064-6, MR 1007713.
  9. Žitnik, Arjana; Horvat, Boris; Pisanski, Tomaž (2010), All generalized Petersen graphs are unit-distance graphs (PDF), IMFM preprints, vol. 1109, archived from the original (PDF) on 2018-07-24, retrieved 2017-04-07.
  10. Steimle, Alice; Staton, William (2009), "The isomorphism classes of the generalized Petersen graphs", Discrete Mathematics, 309 (1): 231–237, doi:10.1016/j.disc.2007.12.074
  11. Ferrero, Daniela; Hanusch, Sarah (2014), "Component connectivity of generalized Petersen graphs" (PDF), International Journal of Computer Mathematics, 91 (9): 1940–1963, doi:10.1080/00207160.2013.878023, ISSN 0020-7160, archived from the original (PDF) on 2018-10-20, retrieved 2018-10-20
  12. Castagna, Frank; Prins, Geert Caleb Ernst (1972), "Every generalized Petersen graph has a Tait coloring", Pacific Journal of Mathematics, 40 (1): 53–58, doi:10.2140/pjm.1972.40.53, ISSN 0030-8730, MR 0304223, Zbl 0236.05106
  13. Bollobás, Béla (2004), Extremal Graph Theory, Dover, p. 233. Reprint of 1978 Academic Press edition.
  14. Castagna, Frank; Prins, Geert (1972), "Every Generalized Petersen Graph has a Tait Coloring", Pacific Journal of Mathematics, 40: 53–58, doi:10.2140/pjm.1972.40.53.
  15. Karami, Hamed (2022), "Perfect 2-colorings of the generalized Petersen graph GP(n,3)", Electronic Journal of Graph Theory and Applications, 10: 239–245, arXiv:2009.07120, doi:10.5614/ejgta.2022.10.1.16.
Categories: