In geometry, a Goursat tetrahedron is a tetrahedral fundamental domain of a Wythoff construction. Each tetrahedral face represents a reflection hyperplane on 3-dimensional surfaces: the 3-sphere, Euclidean 3-space, and hyperbolic 3-space. Coxeter named them after Édouard Goursat who first looked into these domains. It is an extension of the theory of Schwarz triangles for Wythoff constructions on the sphere.
Graphical representation
A Goursat tetrahedron can be represented graphically by a tetrahedral graph, which is in a dual configuration of the fundamental domain tetrahedron. In the graph, each node represents a face (mirror) of the Goursat tetrahedron. Each edge is labeled by a rational value corresponding to the reflection order, being π/dihedral angle.
A 4-node Coxeter-Dynkin diagram represents this tetrahedral graph with order-2 edges hidden. If many edges are order 2, the Coxeter group can be represented by a bracket notation.
Existence requires each of the 3-node subgraphs of this graph, (p q r), (p u s), (q t u), and (r s t), must correspond to a Schwarz triangle.
Extended symmetry
|
|
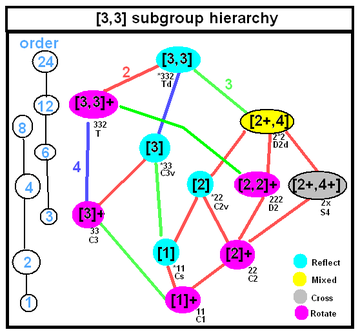
| The symmetry of a Goursat tetrahedron can be tetrahedral symmetry of any subgroup symmetry shown in this tree, with subgroups below with subgroup indices labeled in the colored edges. | |
An extended symmetry of the Goursat tetrahedron is a semidirect product of the Coxeter group symmetry and the fundamental domain symmetry (the Goursat tetrahedron in these cases). Coxeter notation supports this symmetry as double-brackets like ] means full Coxeter group symmetry , with Y as a symmetry of the Goursat tetrahedron. If Y is a pure reflective symmetry, the group will represent another Coxeter group of mirrors. If there is only one simple doubling symmetry, Y can be implicit like ] with either reflectional or rotational symmetry depending on the context.
The extended symmetry of each Goursat tetrahedron is also given below. The highest possible symmetry is that of the regular tetrahedron as , and this occurs in the prismatic point group or and the paracompact hyperbolic group .
See Tetrahedron#Isometries of irregular tetrahedra for 7 lower symmetry isometries of the tetrahedron.
Whole number solutions
The following sections show all of the whole number Goursat tetrahedral solutions on the 3-sphere, Euclidean 3-space, and Hyperbolic 3-space. The extended symmetry of each tetrahedron is also given.
The colored tetrahedal diagrams below are vertex figures for omnitruncated polytopes and honeycombs from each symmetry family. The edge labels represent polygonal face orders, which is double the Coxeter graph branch order. The dihedral angle of an edge labeled 2n is π/n. Yellow edges labeled 4 come from right angle (unconnected) mirror nodes in the Coxeter diagram.
3-sphere (finite) solutions
The solutions for the 3-sphere with density 1 solutions are: (Uniform polychora)
| Coxeter group and diagram |
 
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|---|
| Group symmetry order | 16 | 8p | 4pq | 4p | 48 | 96 | 240 |
| Tetrahedron symmetry |
(order 24) 
|
(order 4) 
|
(order 4)
|
(order 8) 
|
(order 2) 
|
(order 1) 
|
(order 1)
|
| Extended symmetry | ] =
|
] = 
|
] =
|
] =]
|
] =
|
|
|
| Extended symmetry order | 384 | 32p | 16pq | 32p | 96 | 96 | 240 |
Euclidean (affine) 3-space solutions
Density 1 solutions: Convex uniform honeycombs:
| Graph type | Linear Orthoscheme |
Tri-dental Plagioscheme |
Loop Cycloscheme |
Prismatic | Degenerate | ||
|---|---|---|---|---|---|---|---|
| Coxeter group Coxeter diagram |
|
 
|
 
|
|
|
|
|
| Vertex figure of omnitruncated honeycombs | |||||||
| Tetrahedron |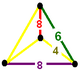 
|
|
|
||||
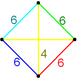
| Tetrahedron Symmetry |
(order 2) 
|
(order 2)
|
(order 8)
|
(order 2)
|
(order 1)
|
(order 6) 
|
(order 8)
|
| Extended symmetry | ]  
|
] =
|
] =]
|
] =
|
|
] =
|
] =]
|
Compact hyperbolic 3-space solutions
Density 1 solutions: (Convex uniform honeycombs in hyperbolic space) (Coxeter diagram#Compact (Lannér simplex groups))
| Graph type | Linear | Tri-dental | |||||
|---|---|---|---|---|---|---|---|
| Coxeter group Coxeter diagram |
|
|
|
|
|||
| Vertex figures of omnitruncated honeycombs | |||||||
| Tetrahedron | 
|
|
|
|
|||
| Tetrahedron Symmetry |
(order 2)
|
(order 1)
|
(order 2)
|
(order 2)
|
|||
| Extended symmetry | ] 
|
|
]
|
] =
|
|||
| Graph type | Loop | ||||||
| Coxeter group Coxeter diagram |
|
|
|
|
| ||
| Vertex figures of omnitruncated honeycombs | |||||||
| Tetrahedron | 
|
|
|
|
| ||
| Tetrahedron Symmetry |
(order 2)
|
(order 4) 
|
(order 2)
|
(order 2)
|
(order 4)
| ||
| Extended symmetry | ]
|
]
|
]
|
]
|
]
| ||
Paracompact hyperbolic 3-space solutions
Density 1 solutions: (See Coxeter diagram#Paracompact (Koszul simplex groups))
| Graph type | Linear graphs | |||||||
|---|---|---|---|---|---|---|---|---|
| Coxeter group and diagram |
|
|
|
|
|
|
| |
| Tetrahedron symmetry |
(order 1)
|
(order 2)
|
(order 1)
|
(order 1)
|
(order 2)
|
(order 1)
|
(order 2)
| |
| Extended symmetry |
|
]
|
|
|
]
|
|
]
| |
| Graph type | Loop graphs | |||||||
| Coxeter group and diagram |
|
|
|
|
|
|
|
|
| Tetrahedron symmetry |
(order 4)
|
(order 2)
|
(order 2)
|
(order 8)
|
(order 2)
|
(order 2)
|
(order 2)
|
(order 4)
|
| Extended symmetry | ] =
|
] =  
|
]
|
] =]
|
]
|
]
|
]
|
]
|
| Graph type | Tri-dental | Loop-n-tail | Simplex | |||||
| Coxeter group and diagram |
|
|
|
|
|
|
|
|
| Tetrahedron symmetry |
(order 2)
|
(order 2)
|
(order 6)
|
(order 2)
|
(order 2)
|
(order 2)
|
(order 2)
|
(order 24)
|
| Extended symmetry | ] =
|
] =
|
] =
|
] =
|
] =
|
] =
|
] =
|
] =
|
Rational solutions
There are hundreds of rational solutions for the 3-sphere, including these 6 linear graphs which generate the Schläfli-Hess polychora, and 11 nonlinear ones from Coxeter:
Linear graphs
|
Loop-n-tail graphs:
|
In all, there are 59 sporadic tetrahedra with rational angles, and 2 infinite families.
See also
- Point group for n-simplex solutions on (n-1)-sphere.
References
- https://arxiv.org/abs/2011.14232 Space vectors forming rational angles, Kiran S. Kedlaya, Alexander Kolpakov, Bjorn Poonen, Michael Rubinstein, 2020
- Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8 (page 280, Goursat's tetrahedra)
- Norman Johnson The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966) He proved the enumeration of the Goursat tetrahedra by Coxeter is complete
- Goursat, Edouard, Sur les substitutions orthogonales et les divisions régulières de l'espace, Annales Scientifiques de l'École Normale Supérieure, Sér. 3, 6 (1889), (pp. 9–102, pp. 80–81 tetrahedra)
- Klitzing, Richard. "Dynkin Diagrams Goursat tetrahedra".
- Norman Johnson, Geometries and Transformations (2018), Chapters 11,12,13
- N. W. Johnson, R. Kellerhals, J. G. Ratcliffe, S. T. Tschantz, The size of a hyperbolic Coxeter simplex, Transformation Groups 1999, Volume 4, Issue 4, pp 329–353