Misplaced Pages

Flattenability in some ${\displaystyle d}$-dimensional normed vector space is a property of graphs which states that any embedding, or drawing, of the graph in some high dimension ${\displaystyle d'}$ can be "flattened" down to live in ${\displaystyle d}$-dimensions, such that the distances between pairs of points connected by edges are preserved. A graph ${\displaystyle G}$ is ${\displaystyle d}$-flattenable if every distance constraint system (DCS) with ${\displaystyle G}$ as its constraint graph has a ${\displaystyle d}$-dimensional framework. Flattenability was first called realizability, but the name was changed to avoid confusion with a graph having some DCS with a ${\displaystyle d}$-dimensional framework.

Flattenability has connections to structural rigidity, tensegrities, Cayley configuration spaces, and a variant of the graph realization problem.

Definitions

A distance constraint system ${\displaystyle (G,\delta )}$, where ${\displaystyle G=(V,E)}$ is a graph and ${\displaystyle \delta :E\rightarrow \mathbb {R} ^{|E|}}$ is an assignment of distances onto the edges of ${\displaystyle G}$, is ${\displaystyle d}$-flattenable in some normed vector space ${\displaystyle \mathbb {R} ^{d}}$ if there exists a framework of ${\displaystyle (G,\delta )}$ in ${\displaystyle d}$-dimensions.

A graph ${\displaystyle G=(V,E)}$ is ${\displaystyle d}$-flattenable in ${\displaystyle \mathbb {R} ^{d}}$ if every distance constraint system with ${\displaystyle G}$ as its constraint graph is ${\displaystyle d}$-flattenable.

Flattenability can also be defined in terms of Cayley configuration spaces; see connection to Cayley configuration spaces below.

Properties

Closure under subgraphs. Flattenability is closed under taking subgraphs. To see this, observe that for some graph ${\displaystyle G}$, all possible embeddings of a subgraph ${\displaystyle H}$ of ${\displaystyle G}$ are contained in the set of all embeddings of ${\displaystyle G}$.

Minor-closed. Flattenability is a minor-closed property by a similar argument as above.

Flattening dimension. The flattening dimension of a graph ${\displaystyle G}$ in some normed vector space is the lowest dimension ${\displaystyle d}$ such that ${\displaystyle G}$ is ${\displaystyle d}$-flattenable. The flattening dimension of a graph is closely related to its gram dimension. The following is an upper-bound on the flattening dimension of an arbitrary graph under the ${\displaystyle l_{2}}$-norm.

Theorem. The flattening dimension of a graph ${\displaystyle G=\left(V,E\right)}$ under the ${\displaystyle l_{2}}$-norm is at most ${\displaystyle O\left({\sqrt {\left|E\right|}}\right)}$.

For a detailed treatment of this topic, see Chapter 11.2 of Deza & Laurent.

Euclidean flattenability

This section concerns flattenability results in Euclidean space, where distance is measured using the ${\displaystyle l_{2}}$ norm, also called the Euclidean norm.

1-flattenable graphs

The following theorem is folklore and shows that the only forbidden minor for 1-flattenability is the complete graph ${\displaystyle K_{3}}$.

Theorem. A graph is 1-flattenable if and only if it is a forest.

Proof. A proof can be found in Belk & Connelly. For one direction, a forest is a collection of trees, and any distance constraint system whose graph is a tree can be realized in 1-dimension. For the other direction, if a graph ${\displaystyle G}$ is not a forest, then it has the complete graph ${\displaystyle K_{3}}$ as a subgraph. Consider the DCS that assigns the distance 1 to the edges of the ${\displaystyle K_{4}}$ subgraph and the distance 0 to all other edges. This DCS has a realization in 2-dimensions as the 1-skeleton of a triangle, but it has no realization in 1-dimension.

This proof allowed for distances on edges to be 0, but the argument holds even when this is not allowed. See Belk & Connelly for a detailed explanation.

2-flattenable graphs

The following theorem is folklore and shows that the only forbidden minor for 2-flattenability is the complete graph ${\displaystyle K_{4}}$.

Theorem. A graph is 2-flattenable if and only if it is a partial 2-tree.

Proof. A proof can be found in Belk & Connelly. For one direction, since flattenability is closed under taking subgraphs, it is sufficient to show that 2-trees are 2-flattenable. A 2-tree with ${\displaystyle n}$ vertices can be constructed recursively by taking a 2-tree with ${\displaystyle n-1}$ vertices and connecting a new vertex to the vertices of an existing edge. The base case is the ${\displaystyle K_{3}}$. Proceed by induction on the number of vertices ${\displaystyle n}$. When ${\displaystyle n=3}$, consider any distance assignment ${\displaystyle \delta }$ on the edges ${\displaystyle K_{3}}$. Note that if ${\displaystyle \delta }$ does not obey the triangle inequality, then this DCS does not have a realization in any dimension. Without loss of generality, place the first vertex ${\displaystyle v_{1}}$ at the origin and the second vertex ${\displaystyle v_{2}}$ along the x-axis such that ${\displaystyle \delta _{12}}$ is satisfied. The third vertex ${\displaystyle v_{3}}$ can be placed at an intersection of the circles with centers ${\displaystyle v_{1}}$ and ${\displaystyle v_{2}}$ and radii ${\displaystyle \delta _{13}}$ and ${\displaystyle \delta _{23}}$ respectively. This method of placement is called a ruler and compass construction. Hence, ${\displaystyle K_{3}}$ is 2-flattenable.

Now, assume a 2-tree with ${\displaystyle k}$ vertices is 2-flattenable. By definition, a 2-tree with ${\displaystyle k+1}$ vertices is a 2-tree with ${\displaystyle k}$ vertices, say ${\displaystyle T}$, and an additional vertex ${\displaystyle u}$ connected to the vertices of an existing edge in ${\displaystyle T}$. By the inductive hypothesis, ${\displaystyle T}$ is 2-flattenable. Finally, by a similar ruler and compass construction argument as in the base case, ${\displaystyle u}$ can be placed such that it lies in the plane. Thus, 2-trees are 2-flattenable by induction.

If a graph ${\displaystyle G}$ is not a partial 2-tree, then it contains ${\displaystyle K_{4}}$ as a minor. Assigning the distance of 1 to the edges of the ${\displaystyle K_{4}}$ minor and the distance of 0 to all other edges yields a DCS with a realization in 3-dimensions as the 1-skeleton of a tetrahedra. However, this DCS has no realization in 2-dimensions: when attempting to place the fourth vertex using a ruler and compass construction, the three circles defined by the fourth vertex do not all intersect.

Example. Consider the graph in figure 2. Adding the edge ${\displaystyle {\bar {AC}}}$ turns it into a 2-tree; hence, it is a partial 2-tree. Thus, it is 2-flattenable.

Example. The wheel graph ${\displaystyle W_{5}}$ contains ${\displaystyle K_{4}}$ as a minor. Thus, it is not 2-flattenable.

3-flattenable graphs

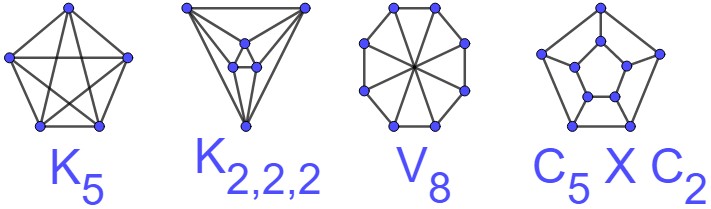
The class of 3-flattenable graphs strictly contains the class of partial 3-trees. More precisely, the forbidden minors for partial 3-trees are the complete graph ${\displaystyle K_{5}}$, the 1-skeleton of the octahedron ${\displaystyle K_{2,2,2}}$, ${\displaystyle V_{8}}$, and ${\displaystyle C_{5}\times C_{2}}$, but ${\displaystyle V_{8}}$, and ${\displaystyle C_{5}\times C_{2}}$ are 3-flattenable. These graphs are shown in Figure 3. Furthermore, the following theorem from Belk & Connelly shows that the only forbidden minors for 3-flattenability are ${\displaystyle K_{5}}$ and ${\displaystyle K_{2,2,2}}$.

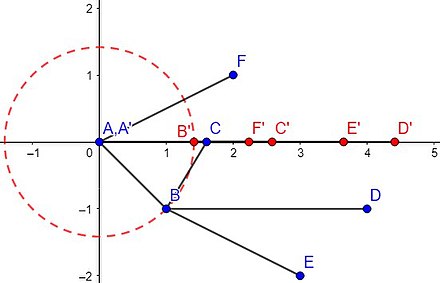
Theorem. A graph is 3-flattenable if and only if it does not have ${\displaystyle K_{5}}$ or ${\displaystyle K_{2,2,2}}$ as a minor.

Proof Idea: The proof given in Belk & Connelly assumes that ${\displaystyle V_{8}}$, and ${\displaystyle C_{5}\times C_{2}}$ are 3-realizable. This is proven in the same article using mathematical tools from rigidity theory, specifically those concerning tensegrities. The complete graph ${\displaystyle K_{5}}$ is not 3-flattenable, and the same argument that shows ${\displaystyle K_{4}}$ is not 2-flattenable and ${\displaystyle K_{3}}$ is not 1-flattenable works here: assigning the distance 1 to the edges of ${\displaystyle K_{5}}$ yields a DCS with no realization in 3-dimensions. Figure 4 gives a visual proof that the graph ${\displaystyle K_{2,2,2}}$ is not 3-flattenable. Vertices 1, 2, and 3 form a degenerate triangle. For the edges between vertices 1- 5, edges ${\displaystyle (1,4)}$ and ${\displaystyle (3,4)}$ are assigned the distance ${\displaystyle {\sqrt {2}}}$ and all other edges are assigned the distance 1. Vertices 1- 5 have unique placements in 3-dimensions, up to congruence. Vertex 6 has 2 possible placements in 3-dimensions: 1 on each side of the plane ${\displaystyle \Pi }$ defined by vertices 1, 2, and 4. Hence, the edge ${\displaystyle (5,6)}$ has two distance values that can be realized in 3-dimensions. However, vertex 6 can revolve around the plane ${\displaystyle \Pi }$ in 4-dimensions while satisfying all constraints, so the edge ${\displaystyle (5,6)}$ has infinitely many distance values that can only be realized in 4-dimensions or higher. Thus, ${\displaystyle K_{2,2,2}}$ is not 3-flattenable. The fact that these graphs are not 3-flattenable proves that any graph with either ${\displaystyle K_{5}}$ or ${\displaystyle K_{2,2,2}}$ as a minor is not 3-flattenable.

The other direction shows that if a graph ${\displaystyle G}$ does not have ${\displaystyle K_{5}}$ or ${\displaystyle K_{2,2,2}}$ as a minor, then ${\displaystyle G}$ can be constructed from partial 3-trees, ${\displaystyle V_{8}}$, and ${\displaystyle C_{5}\times C_{2}}$ via 1-sums, 2-sums, and 3-sums. These graphs are all 3-flattenable and these operations preserve 3-flattenability, so ${\displaystyle G}$ is 3-flattenable.

The techniques in this proof yield the following result from Belk & Connelly.

Theorem. Every 3-realizable graph is a subgraph of a graph that can be obtained by a sequence of 1-sums, 2-sums, and 3-sums of the graphs ${\displaystyle K_{4}}$, ${\displaystyle V_{8}}$, and ${\displaystyle C_{5}\times C_{2}}$.

Example. The previous theorem can be applied to show that the 1-skeleton of a cube is 3-flattenable. Start with the graph ${\displaystyle K_{4}}$, which is the 1-skeleton of a tetrahedron. On each face of the tetrahedron, perform a 3-sum with another ${\displaystyle K_{4}}$ graph, i.e. glue two tetrahedra together on their faces. The resulting graph contains the cube as a subgraph and is 3-flattenable.

In higher dimensions

Giving a forbidden minor characterization of ${\displaystyle d}$-flattenable graphs, for dimension ${\displaystyle d>3}$, is an open problem. For any dimension ${\displaystyle d}$, ${\displaystyle K_{d+2}}$ and the 1-skeleton of the ${\displaystyle d}$-dimensional analogue of an octahedron are forbidden minors for ${\displaystyle d}$-flattenability. It is conjectured that the number of forbidden minors for ${\displaystyle d}$-flattenability grows asymptotically to the number of forbidden minors for partial ${\displaystyle d}$-trees, and there are over ${\displaystyle 75}$ forbidden minors for partial 4-trees.

An alternative characterization of ${\displaystyle d}$-flattenable graphs relates flattenability to Cayley configuration spaces. See the section on the connection to Cayley configuration spaces.

Connection to the graph realization problem

Given a distance constraint system and a dimension ${\displaystyle d}$, the graph realization problem asks for a ${\displaystyle d}$-dimensional framework of the DCS, if one exists. There are algorithms to realize ${\displaystyle d}$-flattenable graphs in ${\displaystyle d}$-dimensions, for ${\displaystyle d\leq 3}$, that run in polynomial time in the size of the graph. For ${\displaystyle d=1}$, realizing each tree in a forest in 1-dimension is trivial to accomplish in polynomial time. An algorithm for ${\displaystyle d=2}$ is mentioned in Belk & Connelly. For ${\displaystyle d=3}$, the algorithm in So & Ye obtains a framework ${\displaystyle r}$ of a DCS using semidefinite programming techniques and then utilizes the "folding" method described in Belk to transform ${\displaystyle r}$ into a 3-dimensional framework.

Flattenability under p-norms

This section concerns flattenability results for graphs under general ${\displaystyle p}$-norms, for ${\displaystyle 1\leq p\leq \infty }$.

Connection to algebraic geometry

Determining the flattenability of a graph under a general ${\displaystyle p}$-norm can be accomplished using methods in algebraic geometry, as suggested in Belk & Connelly. The question of whether a graph ${\displaystyle G=(V,E)}$ is ${\displaystyle d}$-flattenable is equivalent to determining if two semi-algebraic sets are equal. One algorithm to compare two semi-algebraic sets takes ${\displaystyle (4|E|)^{O\left(nd|V|^{2}\right)}}$ time.

Connection to Cayley configuration spaces

For general ${\displaystyle l_{p}}$-norms, there is a close relationship between flattenability and Cayley configuration spaces. The following theorem and its corollary are found in Sitharam & Willoughby.

Theorem. A graph ${\displaystyle G}$ is ${\displaystyle d}$-flattenable if and only if for every subgraph ${\displaystyle H=G\setminus F}$ of ${\displaystyle G}$ resulting from removing a set of edges ${\displaystyle F}$ from ${\displaystyle G}$ and any ${\displaystyle l_{p}^{p}}$-distance vector ${\displaystyle \delta _{H}}$ such that the DCS ${\displaystyle (H,\delta _{H})}$ has a realization, the ${\displaystyle d}$-dimensional Cayley configuration space of ${\displaystyle (H,\delta _{H})}$ over ${\displaystyle F}$ is convex.

Corollary. A graph ${\displaystyle G}$ is not ${\displaystyle d}$-flattenable if there exists some subgraph ${\displaystyle H=G\setminus F}$ of ${\displaystyle G}$ and some ${\displaystyle l_{p}^{p}}$-distance vector ${\displaystyle \delta }$ such that the ${\displaystyle d}$-dimensional Cayley configuration space of ${\displaystyle (H,\delta _{H})}$ over ${\displaystyle F}$ is not convex.

2-Flattenability under the l₁ and l_∞ norms

The ${\displaystyle l_{1}}$ and ${\displaystyle l_{\infty }}$ norms are equivalent up to rotating axes in 2-dimensions, so 2-flattenability results for either norm hold for both. This section uses the ${\displaystyle l_{1}}$-norm. The complete graph ${\displaystyle K_{4}}$ is 2-flattenable under the ${\displaystyle l_{1}}$-norm and ${\displaystyle K_{5}}$ is 3-flattenable, but not 2-flattenable. These facts contribute to the following results on 2-flattenability under the ${\displaystyle l_{1}}$-norm found in Sitharam & Willoughby.

Observation. The set of 2-flattenable graphs under the ${\displaystyle l_{1}}$-norm (and ${\displaystyle l_{\infty }}$-norm) strictly contains the set of 2-flattenable graphs under the ${\displaystyle l_{2}}$-norm.

Theorem. A 2-sum of 2-flattenable graphs is 2-flattenable if and only if at most one graph has a ${\displaystyle K_{4}}$ minor.

The fact that ${\displaystyle K_{4}}$ is 2-flattenable but ${\displaystyle K_{5}}$ is not has implications on the forbidden minor characterization for 2-flattenable graphs under the ${\displaystyle l_{1}}$-norm. Specifically, the minors of ${\displaystyle K_{5}}$ could be forbidden minors for 2-flattenability. The following results explore these possibilities and give the complete set of forbidden minors.

Theorem. The banana graph, or ${\displaystyle K_{5}}$ with one edge removed, is not 2-flattenable.

Observation. The graph obtained by removing two edges that are incident to the same vertex from ${\displaystyle K_{5}}$ is 2-flattenable.

Observation. Connected graphs on 5 vertices with 7 edges are 2-flattenable.

The only minor of ${\displaystyle K_{5}}$ left is the wheel graph ${\displaystyle W_{5}}$, and the following result shows that this is one of the forbidden minors.

Theorem. A graph is 2-flattenable under the ${\displaystyle l_{1}}$- or ${\displaystyle l_{\infty }}$-norm if and only if it does not have either of the following graphs as minors:

• the wheel graph ${\displaystyle W_{5}}$ or
• the graph obtained by taking the 2-sum of two copies of ${\displaystyle K_{4}}$ and removing the shared edge.

Connection to structural rigidity

This section relates flattenability to concepts in structural (combinatorial) rigidity theory, such as the rigidity matroid. The following results concern the ${\displaystyle l_{p}^{p}}$-distance cone ${\displaystyle \Phi _{n,l_{p}}}$, i.e., the set of all ${\displaystyle l_{p}^{p}}$-distance vectors that can be realized as a configuration of ${\displaystyle n}$ points in some dimension. A proof that this set is a cone can be found in Ball. The ${\displaystyle d}$-stratum of this cone ${\displaystyle \Phi _{n,l_{p}}^{d}}$ are the vectors that can be realized as a configuration of ${\displaystyle n}$ points in ${\displaystyle d}$-dimensions. The projection of ${\displaystyle \Phi _{n,l_{p}}}$ or ${\displaystyle \Phi _{n,l_{p}}^{d}}$ onto the edges of a graph ${\displaystyle G}$ is the set of ${\displaystyle l_{p}^{p}}$ distance vectors that can be realized as the edge-lengths of some embedding of ${\displaystyle G}$.

A generic property of a graph ${\displaystyle G}$ is one that almost all frameworks of distance constraint systems, whose graph is ${\displaystyle G}$, have. A framework of a DCS ${\displaystyle (G,\delta )}$ under an ${\displaystyle l_{p}}$-norm is a generic framework (with respect to ${\displaystyle d}$-flattenability) if the following two conditions hold:

1. there is an open neighborhood ${\displaystyle \Omega }$ of ${\displaystyle \delta }$ in the interior of the cone ${\displaystyle \Phi _{n,l_{p}}}$, and
2. the framework is ${\displaystyle d}$-flattenable if and only if all frameworks in ${\displaystyle \Omega }$ are ${\displaystyle d}$-flattenable.

Condition (1) ensures that the neighborhood ${\displaystyle \Omega }$ has full rank. In other words, ${\displaystyle \Omega }$ has dimension equal to the flattening dimension of the complete graph ${\displaystyle K_{n}}$ under the ${\displaystyle l_{p}}$-norm. See Kitson for a more detailed discussion of generic framework for ${\displaystyle l_{p}}$-norms. The following results are found in Sitharam & Willoughby.

Theorem. A graph ${\displaystyle G}$ is ${\displaystyle d}$-flattenable if and only if every generic framework of ${\displaystyle G}$ is ${\displaystyle d}$-flattenable.

Theorem. ${\displaystyle d}$-flattenability is not a generic property of graphs, even for the ${\displaystyle l_{2}}$-norm.

Theorem. A generic ${\displaystyle d}$-flattenable framework of a graph ${\displaystyle G}$ exists if and only if ${\displaystyle G}$ is independent in the generic ${\displaystyle d}$-dimensional rigidity matroid.

Corollary. A graph ${\displaystyle G}$ is ${\displaystyle d}$-flattenable only if ${\displaystyle G}$ is independent in the ${\displaystyle d}$-dimensional rigidity matroid.

Theorem. For general ${\displaystyle l_{p}}$-norms, a graph ${\displaystyle G}$ is

1. independent in the generic ${\displaystyle d}$-dimensional rigidity matroid if and only if the projection of the ${\displaystyle d}$-stratum ${\displaystyle \Phi _{n,l_{p}}^{d}}$ onto the edges of ${\displaystyle G}$ has dimension equal to the number of edges of ${\displaystyle G}$;
2. maximally independent in the generic ${\displaystyle d}$-dimensional rigidity matroid if and only if projecting the ${\displaystyle d}$-stratum ${\displaystyle \Phi _{n,l_{p}}^{d}}$ onto the edges of ${\displaystyle G}$ preserves its dimension and this dimension is equal to the number of edges of ${\displaystyle G}$;
3. rigid in ${\displaystyle d}$-dimensions if and only if projecting the ${\displaystyle d}$-stratum ${\displaystyle \Phi _{n,l_{p}}^{d}}$ onto the edges of ${\displaystyle G}$ preserves its dimension;
4. not independent in the generic ${\displaystyle d}$-dimensional rigidity matroid if and only if the dimension of the projection of the ${\displaystyle d}$-stratum ${\displaystyle \Phi _{n,l_{p}}^{d}}$ onto the edges of ${\displaystyle G}$ is strictly less than the minimum of the dimension of ${\displaystyle \Phi _{n,l_{p}}^{d}}$ and the number of edges of ${\displaystyle G}$.

References

1. ^ Belk, Maria; Connelly, Robert (2007). "Realizability of Graphs". Discrete & Computational Geometry. 37 (2): 125–137. doi:10.1007/s00454-006-1284-5. S2CID 12755057.
2. ^ Sitharam, M.; Willoughby, J. (2014). "On Flattenability of Graphs". Automated Deduction in Geometry. Lecture Notes in Computer Science. Vol. 9201. pp. 129–148. doi:10.1007/978-3-319-21362-0_9. ISBN 978-3-319-21361-3. S2CID 23208.
3. Laurent, Monique; Varvitsiotis, Antonios (2012). "The Gram Dimension of a Graph". Combinatorial Optimization. Lecture Notes in Computer Science. Vol. 7422. pp. 356–367. doi:10.1007/978-3-642-32147-4_32. ISBN 978-3-642-32146-7. S2CID 18567150.
4. Barvinok, A. (1995). "Problems of distance geometry and convex properties of quadratic maps". Discrete & Computational Geometry. 13 (2): 189–202. doi:10.1007/BF02574037. S2CID 20628306.
5. ^ Deza, Michel; Laurent, Monique (1997). Geometry of Cuts and Metrics. Springer-Verlag Berlin Heidelberg. doi:10.1007/978-3-642-04295-9. ISBN 978-3-540-61611-5.
6. ^ Belk, Maria (2007). "Realizability of Graphs in Three Dimensions". Discrete & Computational Geometry. 37 (2): 139–162. doi:10.1007/s00454-006-1285-4. S2CID 20238879.
7. ^ Sitharam, Meera; Gao, Heping (2010). "Characterizing Graphs with Convex and Connected Cayley Configuration Spaces". Discrete & Computational Geometry. 43 (3): 594–625. doi:10.1007/s00454-009-9160-8. S2CID 35819450.
8. So, Anthony Man-Cho; Ye, Yinyu (2006). "A semidefinite programming approach to tensegrity theory and realizability of graphs". Proceedings of the seventeenth annual ACM-SIAM symposium on Discrete algorithm - SODA '06. pp. 766–775. doi:10.1145/1109557.1109641. ISBN 0898716055. S2CID 10134807.
9. Basu, Saugata; Pollack, Richard; Marie-Francoise, Roy (2003). "Existential Theory of the Reals". Algorithms in Real Algebraic Geometry. Algorithms and Computation in Mathematics. Vol. 10. Springer, Berlin, Heidelberg. doi:10.1007/3-540-33099-2_14. ISBN 978-3-540-33098-1.
10. Witsenhausen, Hans S. (1986). "Minimum dimension embedding of finite metric spaces". Journal of Combinatorial Theory. Series A. 42 (2): 184–199. doi:10.1016/0097-3165(86)90089-0.
11. Fiorini, Samuel; Huynh, Tony; Joret, Gwenaël; Varvitsiotis, Antonios (2017-01-01). "The Excluded Minors for Isometric Realizability in the Plane". SIAM Journal on Discrete Mathematics. 31 (1): 438–453. arXiv:1511.08054. doi:10.1137/16M1064775. hdl:10356/81454. ISSN 0895-4801. S2CID 2579286.
12. Ball, Keith (1990). "Isometric Embedding in lp-spaces". European Journal of Combinatorics. 11 (4): 305–311. doi:10.1016/S0195-6698(13)80131-X.
13. Kitson, Derek (2015). "Finite and Infinitesimal Rigidity with Polyhedral Norms". Discrete & Computational Geometry. 54 (2): 390–411. arXiv:1401.1336. doi:10.1007/s00454-015-9706-x. S2CID 15520982.

• Graphs
• Graph theory