| Great ditrigonal icosidodecahedron | |
|---|---|
| |
| Type | Uniform star polyhedron |
| Elements | F = 32, E = 60 V = 20 (χ = −8) |
| Faces by sides | 20{3}+12{5} |
| Coxeter diagram |    
|
| Wythoff symbol | 3/2 | 3 5 3 | 3/2 5 3 | 3 5/4 3/2 | 3/2 5/4 |
| Symmetry group | Ih, , *532 |
| Index references | U47, C61, W87 |
| Dual polyhedron | Great triambic icosahedron |
| Vertex figure |  ((3.5))/2 |
| Bowers acronym | Gidtid |
In geometry, the great ditrigonal icosidodecahedron (or great ditrigonary icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U47. It has 32 faces (20 triangles and 12 pentagons), 60 edges, and 20 vertices. It has 4 Schwarz triangle equivalent constructions, for example Wythoff symbol 3 | 3 5⁄4 gives Coxeter diagram 
= 
. It has extended Schläfli symbol a{5⁄2,3} or c{3,5⁄2}, as an altered great stellated dodecahedron or converted great icosahedron.
Its circumradius is times the length of its edge, a value it shares with the cube.
times the length of its edge, a value it shares with the Related polyhedra
Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron (having the triangular faces in common), the ditrigonal dodecadodecahedron (having the pentagonal faces in common), and the regular compound of five cubes.
| a{5,3} | a{5/2,3} | b{5,5/2} |
|---|---|---|
 = 
|
=
|
|
 Small ditrigonal icosidodecahedron |
Great ditrigonal icosidodecahedron |
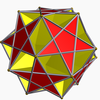 Ditrigonal dodecadodecahedron |
 Dodecahedron (convex hull) |
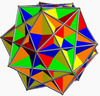 Compound of five cubes |
References
- Maeder, Roman. "47: great ditrigonal icosidodecahedron". MathConsult.
- Weisstein, Eric W (2003), CRC concise encyclopedia of mathematics, Boca Raton: Chapman & Hall/CRC, ISBN 1-58488-347-2
External links
 | This polyhedron-related article is a stub. You can help Misplaced Pages by expanding it. |