Grid classification - Misplaced Pages

This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (August 2019) (Learn how and when to remove this message)

In applied mathematics, a grid or mesh is defined as the set of smaller shapes formed after discretisation of a geometric domain. Meshing has applications in the fields of geography, designing, computational fluid dynamics, and more generally in partial differential equations numerical solving. The geometric domain can be in any dimension. The two-dimensional meshing includes simple polygon, polygon with holes, multiple domain and curved domain. In three dimensions there are three types of inputs. They are simple polyhedron, geometrical polyhedron and multiple polyhedrons. Before defining the mesh type it is necessary to understand elements (their shape and size).

Elements

An element of a mesh is one of the smaller shapes evoked in the introduction. The shape of the elements is of great importance in solving problems in computational fluid dynamics. They are typically based on aspect ratio i.e. the aspect ratio of element decide whether a particular element would be good to use or we should go for another element with different aspect ratio. For example, if the aspect ratio is large the speed of solver reduces while if this ratio is small the solver speed increases. Large aspect ratio has another limitation of leading to interpolation errors. But if the results vary with direction then we use large aspect ratio.

Fluid flow equation and coordinate system

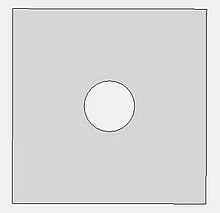
Most of the fluid flow equations are easily solved by discretizing procedures using the Cartesian coordinate system. In this system the implementation of finite volume method is simpler and easier to understand. But most of the engineering problems deal with complex geometries that don’t work well in the Cartesian coordinate system. When the boundary region of the flow does not coincide with the coordinate lines of the structured grid then we can solve the problem by geometry approximation. Figures 1a. and 1b. shows how a cylinder can be approximated with the Cartesian coordinate system.

The curve geometry of cylinder in Cartesian coordinate system is approximated by using stepwise approximation. But this method requires large time and is very tedious to work with. Other than this problem there is one more problem which is the cells inside the solid part of the cylinder, which are called dead cells, are not involved in the calculations so they should be removed, otherwise they would consume extra space in computer or other resources. Stepwise approximation is not smooth and thus leads to significant error, though the grid can be refined by using a fine mesh to cover the wall region but this leads to waste of computer memory resources.

Therefore, there are limitation in using methods in computational fluid dynamics based on simple coordinate system (Cartesian or cylindrical) as these systems fails while modeling of complex geometries like that of an aerofoil, furnaces, gas turbine combustors, IC-engine etc.

Classification of grids in computational fluid dynamics

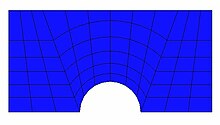
a) Structured curvilinear grid arrangements (vertices having similar neighborhood).

b) Unstructured grid arrangements (vertices having variation in neighborhood).

Structured curvilinear grids

1) Grid points are identified at the intersection of coordinate line.

2) There are fixed number of neighboring grids for interior grid.

3) They can be arranged into an array and can be named by indices I, J, K f (In three dimensions).

These are also known as body-fitted grids and works on the principle of mapping the flow domain onto computational domain with simple shape. The mapping is quite tedious if it involves Complex geometry. In order to model this type of geometry we divide the flow region into various smaller sub domains. All these regions are meshed separately and joined up correctly with the neighbors. This type of arrangement is known as block-structured grid. This type of system is more flexible than the previous one. Two-dimensional structured mesh use quadrilaterals elements, while three-dimension meshes use hexahedra. There are two types of body-fitted coordinate grids:

a) Orthogonal curvilinear coordinate.

In orthogonal mesh the grid lines are perpendicular to intersection. This is shown in Figure 2.

b) Non–orthogonal coordinate.

Figure 3 shows non-orthogonal grids. The figure shows the grid lines do not intersect at 90-degree angle. In both these cases the domain boundaries coincide with the coordinate lines; therefore all the geometrical details can be incorporated. Grids can be refined easily to capture important flow features.

Comparison between Cartesian and curvilinear grids

Comparison between Cartesian and curvilinear grids shows that in Cartesian grid cells are wasted in dealing with objects. The distribution of function is very fine in curvilinear grid. The resources required in curvilinear grids are less as compared to Cartesian grids thus saving much memory. Therefore, we can say that coarse grids are able to capture flow details efficiently.

Disadvantages of curvilinear grids

Difficulties associated with the curvilinear grids are related to equations.

While in Cartesian system the equation can be solved easily with less difficulty, but in curvilinear coordinate system it is difficult to solve the complex equations. Difference between various techniques lies in the fact that what type of grid arrangement is required and the dependent variable that is required in momentum equation. To generate meshes so that it includes all the geometrical features mapping is very important. In mapping physical geometry is mapped with computational geometry.

There are difficulties which we face in generating the body-fitted grids in geometries like IC engine combustion chamber. For example, the valve mapping in internal combustion engine is done very carefully so that the region of one type is mapped carefully with another type of region. There are regions where dense mesh is done deliberately to accommodate complex features. But this results in unnecessary grid resolution which leads to local variation of solution domain.

Block-structured grid

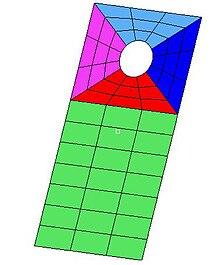
In this type of grid the domain is divided into different regions. Each region has different type of mesh structure. It is also possible that different coordinate system can be used for different regions. This makes the grids far more flexible. This also makes the refinement in the region where the geometry is to be captured more precise. Figure 4 shows the use of block grid technique. The advantages of this technique are that its generation is easy, the equations that we work with are easily discretized and curved boundaries are easily accommodated. Different blocks can be handled with required degree of fineness in mesh. GridPro can create beautiful multiblock structured meshes.

Unstructured grids

In far more complex geometries it is logical to use large number of blocks and therefore it leads to unstructured grids. These are widely accepted in computational fluid dynamics because this gives us far more flexibility and computer resources are also efficiently utilized. In this case two-dimensional unstructured mesh uses triangle elements while three-dimensional uses tetrahedral elements. These are combination of small structured mesh arranged in unstructured pattern. In this type of grid each single cell is treated as a block. There is no structure of coordinate lines that is given by the grid. The advantage of this type of grids is that mesh can be refined wherever needed. This is based on the fact since the control volume can be of any shape therefore restriction on number of adjacent cell is lifted. This uses various combinations of cell shapes. Hybrid grid can also be used. Hybrid grids are those in which mixture of triangular and quadrilateral elements are used to construct grids. In three dimension combination of tetrahedral and hexahedral elements results in hybrid grid. Example of hybrid grid is shown in Figure 5. Unstructured grids reduces the time which is required for meshing and mapping. Therefore, grid generation is faster and easy. Various automatic techniques especially those associated with Finite Element Method also utilize unstructured grids. Mesh refinement and adaption is easy in unstructured grids.

Mesh improvement

This is done by two techniques namely smoothing and flipping. In mesh smoothing the location of mesh vertices are adjusted. While in Flipping the diagonals of triangulated quadrilateral are exchanged. Flipping improves the quality measure of triangles.

References

Patankar, Suhas V. (1980). Numerical Heat Transfer and Fluid FLow. Hemisphere Publishing Corporation. ISBN 0891165223.
Marshall, D., and Ruffin, S.M., " An Embedded Boundary Cartesian Grid Scheme for Viscous Flows using a New Viscous Wall Boundary Condition Treatment,” AIAA Paper 2004-0581, presented at the AIAA 42nd Aerospace Sciences Meeting, January 2004.
Versteeg, H.K.; Malalasekera, W. (2007). An introduction to computational fluid dynamics : the finite volume method (2nd ed.). Harlow: Prentice Hall. ISBN 9780131274983.
Karmna, Steve L. Jr., "Splitfor: A 3D Unstructured Cartesian Prismatic Grid CFD Code for Complex Geometries," AIAA paper 95-0343, presented at the 33rd Aerospace Sciences Meeting and Exhibit, Reno Nevada, January 1995.