Misplaced Pages

Seafloor spreading, or seafloor spread, is a process that occurs at mid-ocean ridges, where new oceanic crust is formed through volcanic activity and then gradually moves away from the ridge.

History of study

Earlier theories by Alfred Wegener and Alexander du Toit of continental drift postulated that continents in motion "plowed" through the fixed and immovable seafloor. The idea that the seafloor itself moves and also carries the continents with it as it spreads from a central rift axis was proposed by Harold Hammond Hess from Princeton University and Robert Dietz of the U.S. Naval Electronics Laboratory in San Diego in the 1960s. The phenomenon is known today as plate tectonics. In locations where two plates move apart, at mid-ocean ridges, new seafloor is continually formed during seafloor spreading.

Significance

Seafloor spreading helps explain continental drift in the theory of plate tectonics. When oceanic plates diverge, tensional stress causes fractures to occur in the lithosphere. The motivating force for seafloor spreading ridges is tectonic plate slab pull at subduction zones, rather than magma pressure, although there is typically significant magma activity at spreading ridges. Plates that are not subducting are driven by gravity sliding off the elevated mid-ocean ridges a process called ridge push. At a spreading center, basaltic magma rises up the fractures and cools on the ocean floor to form new seabed. Hydrothermal vents are common at spreading centers. Older rocks will be found farther away from the spreading zone while younger rocks will be found nearer to the spreading zone.

Spreading rate is the rate at which an ocean basin widens due to seafloor spreading. (The rate at which new oceanic lithosphere is added to each tectonic plate on either side of a mid-ocean ridge is the spreading half-rate and is equal to half of the spreading rate). Spreading rates determine if the ridge is fast, intermediate, or slow. As a general rule, fast ridges have spreading (opening) rates of more than 90 mm/year. Intermediate ridges have a spreading rate of 40–90 mm/year while slow spreading ridges have a rate less than 40 mm/year. The highest known rate was over 200 mm/yr during the Miocene on the East Pacific Rise.

In the 1960s, the past record of geomagnetic reversals of Earth's magnetic field was noticed by observing magnetic stripe "anomalies" on the ocean floor. This results in broadly evident "stripes" from which the past magnetic field polarity can be inferred from data gathered with a magnetometer towed on the sea surface or from an aircraft. The stripes on one side of the mid-ocean ridge were the mirror image of those on the other side. By identifying a reversal with a known age and measuring the distance of that reversal from the spreading center, the spreading half-rate could be computed.

In some locations spreading rates have been found to be asymmetric; the half rates differ on each side of the ridge crest by about five percent. This is thought due to temperature gradients in the asthenosphere from mantle plumes near the spreading center.

Spreading centers

Seafloor spreading occurs at spreading centers, distributed along the crests of mid-ocean ridges. Spreading centers end in transform faults or in overlapping spreading center offsets. A spreading center includes a seismically active plate boundary zone a few kilometers to tens of kilometers wide, a crustal accretion zone within the boundary zone where the ocean crust is youngest, and an instantaneous plate boundary – a line within the crustal accretion zone demarcating the two separating plates. Within the crustal accretion zone is a 1–2 km-wide neovolcanic zone where active volcanism occurs.

Incipient spreading

In the general case, seafloor spreading starts as a rift in a continental land mass, similar to the Red Sea-East Africa Rift System today. The process starts by heating at the base of the continental crust which causes it to become more plastic and less dense. Because less dense objects rise in relation to denser objects, the area being heated becomes a broad dome (see isostasy). As the crust bows upward, fractures occur that gradually grow into rifts. The typical rift system consists of three rift arms at approximately 120-degree angles. These areas are named triple junctions and can be found in several places across the world today. The separated margins of the continents evolve to form passive margins. Hess' theory was that new seafloor is formed when magma is forced upward toward the surface at a mid-ocean ridge.

If spreading continues past the incipient stage described above, two of the rift arms will open while the third arm stops opening and becomes a 'failed rift' or aulacogen. As the two active rifts continue to open, eventually the continental crust is attenuated as far as it will stretch. At this point basaltic oceanic crust and upper mantle lithosphere begins to form between the separating continental fragments. When one of the rifts opens into the existing ocean, the rift system is flooded with seawater and becomes a new sea. The Red Sea is an example of a new arm of the sea. The East African rift was thought to be a failed arm that was opening more slowly than the other two arms, but in 2005 the Ethiopian Afar Geophysical Lithospheric Experiment reported that in the Afar region, September 2005, a 60 km fissure opened as wide as eight meters. During this period of initial flooding the new sea is sensitive to changes in climate and eustasy. As a result, the new sea will evaporate (partially or completely) several times before the elevation of the rift valley has been lowered to the point that the sea becomes stable. During this period of evaporation large evaporite deposits will be made in the rift valley. Later these deposits have the potential to become hydrocarbon seals and are of particular interest to petroleum geologists.

Seafloor spreading can stop during the process, but if it continues to the point that the continent is completely severed, then a new ocean basin is created. The Red Sea has not yet completely split Arabia from Africa, but a similar feature can be found on the other side of Africa that has broken completely free. South America once fit into the area of the Niger Delta. The Niger River has formed in the failed rift arm of the triple junction.

Continued spreading and subduction

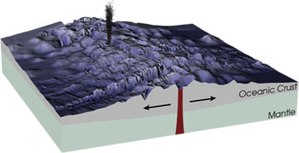
As new seafloor forms and spreads apart from the mid-ocean ridge it slowly cools over time. Older seafloor is, therefore, colder than new seafloor, and older oceanic basins deeper than new oceanic basins due to isostasy. If the diameter of the earth remains relatively constant despite the production of new crust, a mechanism must exist by which crust is also destroyed. The destruction of oceanic crust occurs at subduction zones where oceanic crust is forced under either continental crust or oceanic crust. Today, the Atlantic basin is actively spreading at the Mid-Atlantic Ridge. Only a small portion of the oceanic crust produced in the Atlantic is subducted. However, the plates making up the Pacific Ocean are experiencing subduction along many of their boundaries which causes the volcanic activity in what has been termed the Ring of Fire of the Pacific Ocean. The Pacific is also home to one of the world's most active spreading centers (the East Pacific Rise) with spreading rates of up to 145 ± 4 mm/yr between the Pacific and Nazca plates. The Mid-Atlantic Ridge is a slow-spreading center, while the East Pacific Rise is an example of fast spreading. Spreading centers at slow and intermediate rates exhibit a rift valley while at fast rates an axial high is found within the crustal accretion zone. The differences in spreading rates affect not only the geometries of the ridges but also the geochemistry of the basalts that are produced.

Since the new oceanic basins are shallower than the old oceanic basins, the total capacity of the world's ocean basins decreases during times of active sea floor spreading. During the opening of the Atlantic Ocean, sea level was so high that a Western Interior Seaway formed across North America from the Gulf of Mexico to the Arctic Ocean.

Debate and search for mechanism

At the Mid-Atlantic Ridge (and in other mid-ocean ridges), material from the upper mantle rises through the faults between oceanic plates to form new crust as the plates move away from each other, a phenomenon first observed as continental drift. When Alfred Wegener first presented a hypothesis of continental drift in 1912, he suggested that continents plowed through the ocean crust. This was impossible: oceanic crust is both more dense and more rigid than continental crust. Accordingly, Wegener's theory wasn't taken very seriously, especially in the United States.

At first the driving force for spreading was argued to be convection currents in the mantle. Since then, it has been shown that the motion of the continents is linked to seafloor spreading by the theory of plate tectonics, which is driven by convection that includes the crust itself as well.

The driver for seafloor spreading in plates with active margins is the weight of the cool, dense, subducting slabs that pull them along, or slab pull. The magmatism at the ridge is considered to be passive upwelling, which is caused by the plates being pulled apart under the weight of their own slabs. This can be thought of as analogous to a rug on a table with little friction: when part of the rug is off of the table, its weight pulls the rest of the rug down with it. However, the Mid-Atlantic ridge itself is not bordered by plates that are being pulled into subduction zones, except the minor subduction in the Lesser Antilles and Scotia Arc. In this case the plates are sliding apart over the mantle upwelling in the process of ridge push.

Seafloor global topography: cooling models

The depth of the seafloor (or the height of a location on a mid-ocean ridge above a base-level) is closely correlated with its age (age of the lithosphere where depth is measured). The age-depth relation can be modeled by the cooling of a lithosphere plate or mantle half-space in areas without significant subduction.

Cooling mantle model

In the mantle half-space model, the seabed height is determined by the oceanic lithosphere and mantle temperature, due to thermal expansion. The simple result is that the ridge height or ocean depth is proportional to the square root of its age. Oceanic lithosphere is continuously formed at a constant rate at the mid-ocean ridges. The source of the lithosphere has a half-plane shape (x = 0, z < 0) and a constant temperature T₁. Due to its continuous creation, the lithosphere at x > 0 is moving away from the ridge at a constant velocity v, which is assumed large compared to other typical scales in the problem. The temperature at the upper boundary of the lithosphere (z = 0) is a constant T₀ = 0. Thus at x = 0 the temperature is the Heaviside step function ${\displaystyle T_{1}\cdot \Theta (-z)}$. The system is assumed to be at a quasi-steady state, so that the temperature distribution is constant in time, i.e. ${\displaystyle T=T(x,z).}$

By calculating in the frame of reference of the moving lithosphere (velocity v), which has spatial coordinate ${\displaystyle x'=x-vt,}$ ${\displaystyle T=T(x',z,t).}$ and the heat equation is:

${\displaystyle {\frac {\partial T}{\partial t}}=\kappa \nabla ^{2}T=\kappa {\frac {\partial ^{2}T}{\partial ^{2}z}}+\kappa {\frac {\partial ^{2}T}{\partial ^{2}x'}}}$

where ${\displaystyle \kappa }$ is the thermal diffusivity of the mantle lithosphere.

Since T depends on x' and t only through the combination ${\displaystyle x=x'+vt,}$:

${\displaystyle {\frac {\partial T}{\partial x'}}={\frac {1}{v}}\cdot {\frac {\partial T}{\partial t}}}$

Thus:

${\displaystyle {\frac {\partial T}{\partial t}}=\kappa \nabla ^{2}T=\kappa {\frac {\partial ^{2}T}{\partial ^{2}z}}+{\frac {\kappa }{v^{2}}}{\frac {\partial ^{2}T}{\partial ^{2}t}}}$

It is assumed that ${\displaystyle v}$ is large compared to other scales in the problem; therefore the last term in the equation is neglected, giving a 1-dimensional diffusion equation:

${\displaystyle {\frac {\partial T}{\partial t}}=\kappa {\frac {\partial ^{2}T}{\partial ^{2}z}}}$

with the initial conditions

${\displaystyle T(t=0)=T_{1}\cdot \Theta (-z).}$

The solution for ${\displaystyle z\leq 0}$ is given by the error function:

${\displaystyle T(x',z,t)=T_{1}\cdot \operatorname {erf} \left({\frac {z}{2{\sqrt {\kappa t}}}}\right)}$.

Due to the large velocity, the temperature dependence on the horizontal direction is negligible, and the height at time t (i.e. of sea floor of age t) can be calculated by integrating the thermal expansion over z:

${\displaystyle h(t)=h_{0}+\alpha _{\mathrm {eff} }\int _{0}^{\infty }dz=h_{0}-{\frac {2}{\sqrt {\pi }}}\alpha _{\mathrm {eff} }T_{1}{\sqrt {\kappa t}}}$

where ${\displaystyle \alpha _{\mathrm {eff} }}$ is the effective volumetric thermal expansion coefficient, and h₀ is the mid-ocean ridge height (compared to some reference).

The assumption that v is relatively large is equivalent to the assumption that the thermal diffusivity ${\displaystyle \kappa }$ is small compared to ${\displaystyle L^{2}/A}$, where L is the ocean width (from mid-ocean ridges to continental shelf) and A is the age of the ocean basin.

The effective thermal expansion coefficient ${\displaystyle \alpha _{\mathrm {eff} }}$ is different from the usual thermal expansion coefficient ${\displaystyle \alpha }$ due to isostasic effect of the change in water column height above the lithosphere as it expands or retracts. Both coefficients are related by:

${\displaystyle \alpha _{\mathrm {eff} }=\alpha \cdot {\frac {\rho }{\rho -\rho _{w}}}}$

where ${\displaystyle \rho \sim 3.3\ \mathrm {g} \cdot \mathrm {cm} ^{-3}}$ is the rock density and ${\displaystyle \rho _{0}=1\ \mathrm {g} \cdot \mathrm {cm} ^{-3}}$ is the density of water.

By substituting the parameters by their rough estimates:

${\displaystyle {\begin{aligned}\kappa &\sim 8\cdot 10^{-7}\ \mathrm {m} ^{2}\cdot \mathrm {s} ^{-1}\\\alpha &\sim 4\cdot 10^{-5}\ {}^{\circ }\mathrm {C} ^{-1}\\T_{1}&\sim 1220\ {}^{\circ }\mathrm {C} &&{\text{for the Atlantic and Indian oceans}}\\T_{1}&\sim 1120\ {}^{\circ }\mathrm {C} &&{\text{for the eastern Pacific}}\end{aligned}}}$

gives:

${\displaystyle h(t)\sim {\begin{cases}h_{0}-390{\sqrt {t}}&{\text{for the Atlantic and Indian oceans}}\\h_{0}-350{\sqrt {t}}&{\text{for the eastern Pacific}}\end{cases}}}$

where the height is in meters and time is in millions of years. To get the dependence on x, one must substitute t = x/v ~ Ax/L, where L is the distance between the ridge to the continental shelf (roughly half the ocean width), and A is the ocean basin age.

Rather than height of the ocean floor ${\displaystyle h(t)}$ above a base or reference level ${\displaystyle h_{b}}$, the depth of the ocean ${\displaystyle d(t)}$ is of interest. Because ${\displaystyle d(t)+h(t)=h_{b}}$(with ${\displaystyle h_{b}}$ measured from the ocean surface):

${\displaystyle d(t)=h_{b}-h_{0}+350{\sqrt {t}}}$; for the eastern Pacific for example, where ${\displaystyle h_{b}-h_{0}}$ is the depth at the ridge crest, typically 2600 m.

Cooling plate model

The depth predicted by the square root of seafloor age derived above is too deep for seafloor older than 80 million years. Depth is better explained by a cooling lithosphere plate model rather than the cooling mantle half-space. The plate has a constant temperature at its base and spreading edge. Analysis of depth versus age and depth versus square root of age data allowed Parsons and Sclater to estimate model parameters (for the North Pacific):

~125 km for lithosphere thickness

${\displaystyle T_{1}\thicksim 1350\ {}^{\circ }\mathrm {C} }$ at base and young edge of plate

${\displaystyle \alpha \thicksim 3.2\cdot 10^{-5}\ {}^{\circ }\mathrm {C} ^{-1}}$

Assuming isostatic equilibrium everywhere beneath the cooling plate yields a revised age depth relationship for older sea floor that is approximately correct for ages as young as 20 million years:

${\displaystyle d(t)=6400-3200\exp {\bigl (}-t/62.8{\bigr )}}$ meters

Thus older seafloor deepens more slowly than younger and in fact can be assumed almost constant at ~6400 m depth. Parsons and Sclater concluded that some style of mantle convection must apply heat to the base of the plate everywhere to prevent cooling down below 125 km and lithosphere contraction (seafloor deepening) at older ages. Their plate model also allowed an expression for conductive heat flow, q(t) from the ocean floor, which is approximately constant at ${\displaystyle 1\cdot 10^{-6}\mathrm {cal} \,\mathrm {cm} ^{-2}\mathrm {sec} ^{-1}}$ beyond 120 million years:

${\displaystyle q(t)=11.3/{\sqrt {t}}}$

See also

• Divergent boundary – Linear feature that exists between two tectonic plates that are moving away from each other
• Vine–Matthews–Morley hypothesis – Concept in plate tectonics
• DSV ALVIN the research submersible that explored spreading centers in the Atlantic (Project FAMOUS) and Pacific Oceans (RISE project).

References

1. Hess, H. H. (November 1962). "History of Ocean Basins" (PDF). In A. E. J. Engel; Harold L. James; B. F. Leonard (eds.). Petrologic studies: a volume to honor A. F. Buddington. Boulder, CO: Geological Society of America. pp. 599–620.
2. Dietz, Robert S. (1961). "Continent and Ocean Basin Evolution by Spreading of the Sea Floor". Nature. 190 (4779): 854–857. Bibcode:1961Natur.190..854D. doi:10.1038/190854a0. ISSN 0028-0836. S2CID 4288496.
3. Tan, Yen Joe; Tolstoy, Maya; Waldhauser, Felix; Wilcock, William S. D. (2016). "Dynamics of a seafloor-spreading episode at the East Pacific Rise". Nature. 540 (7632): 261–265. Bibcode:2016Natur.540..261T. doi:10.1038/nature20116. PMID 27842380. S2CID 205251567.
4. ^ Forsyth, Donald; Uyeda, Seiya (1975-10-01). "On the Relative Importance of the Driving Forces of Plate Motion". Geophysical Journal International. 43 (1): 163–200. Bibcode:1975GeoJ...43..163F. doi:10.1111/j.1365-246x.1975.tb00631.x. ISSN 0956-540X.
5. Macdonald, Ken C. (2019), "Mid-Ocean Ridge Tectonics, Volcanism, and Geomorphology", Encyclopedia of Ocean Sciences, Elsevier, pp. 405–419, doi:10.1016/b978-0-12-409548-9.11065-6, ISBN 9780128130827
6. ^ Macdonald, K. C. (1982). "Mid-Ocean Ridges: Fine Scale Tectonic, Volcanic and Hydrothermal Processes Within the Plate Boundary Zone". Annual Review of Earth and Planetary Sciences. 10 (1): 155–190. Bibcode:1982AREPS..10..155M. doi:10.1146/annurev.ea.10.050182.001103.
7. Searle, Roger (2013). Mid-ocean ridges. New York: Cambridge. ISBN 9781107017528. OCLC 842323181.
8. Wilson, Douglas S. (1996-10-15). "Fastest known spreading on the Miocene Cocos-Pacific Plate Boundary". Geophysical Research Letters. 23 (21): 3003–3006. Bibcode:1996GeoRL..23.3003W. doi:10.1029/96GL02893.
9. Vine, F. J.; Matthews, D. H. (1963). "Magnetic Anomalies Over Oceanic Ridges". Nature. 199 (4897): 947–949. Bibcode:1963Natur.199..947V. doi:10.1038/199947a0. S2CID 4296143.
10. Vine, F. J. (1966-12-16). "Spreading of the Ocean Floor: New Evidence". Science. 154 (3755): 1405–1415. Bibcode:1966Sci...154.1405V. doi:10.1126/science.154.3755.1405. ISSN 0036-8075. PMID 17821553. S2CID 44362406.
11. Weissel, Jeffrey K.; Hayes, Dennis E. (1971). "Asymmetric Seafloor Spreading south of Australia". Nature. 231 (5304): 518–522. Bibcode:1971Natur.231..518W. doi:10.1038/231518a0. ISSN 1476-4687. S2CID 4171566.
12. ^ Müller, R. Dietmar; Sdrolias, Maria; Gaina, Carmen; Roest, Walter R. (2008). "Age, spreading rates, and spreading asymmetry of the world's ocean crust: DIGITAL MODELS OF THE WORLD'S OCEAN CRUST". Geochemistry, Geophysics, Geosystems. 9 (4): n/a. Bibcode:2008GGG.....9.4006M. doi:10.1029/2007GC001743. S2CID 15960331.
13. Luyendyk, Bruce P.; Macdonald, Ken C. (1976-06-01). "Spreading center terms and concepts". Geology. 4 (6): 369. Bibcode:1976Geo.....4..369L. doi:10.1130/0091-7613(1976)4<369:sctac>2.0.co;2. ISSN 0091-7613.
14. Daignieres, Marc; Courtillot, Vincent; Bayer, Roger; Tapponnier, Paul (1975). "A model for the evolution of the axial zone of mid-ocean ridges as suggested by icelandic tectonics". Earth and Planetary Science Letters. 26 (2): 222–232. Bibcode:1975E&PSL..26..222D. doi:10.1016/0012-821x(75)90089-8.
15. McClinton, J. Timothy; White, Scott M. (2015-03-01). "Emplacement of submarine lava flow fields: A geomorphological model from the Niños eruption at the Galápagos Spreading Center". Geochemistry, Geophysics, Geosystems. 16 (3): 899–911. Bibcode:2015GGG....16..899M. doi:10.1002/2014gc005632. ISSN 1525-2027.
16. Makris, J.; Ginzburg, A. (1987-09-15). "Sedimentary basins within the Dead Sea and other rift zones The Afar Depression: transition between continental rifting and sea-floor spreading". Tectonophysics. 141 (1): 199–214. Bibcode:1987Tectp.141..199M. doi:10.1016/0040-1951(87)90186-7. S2CID 129438029.
17. Bastow, Ian D.; Keir, Derek; Daly, Eve (2011-06-01). The Ethiopia Afar Geoscientific Lithospheric Experiment (EAGLE): Probing the transition from continental rifting to incipient seafloor spreading. Geological Society of America Special Papers. Vol. 478. pp. 51–76. doi:10.1130/2011.2478(04). hdl:2158/1110145. ISBN 978-0-8137-2478-2. ISSN 0072-1077. {{cite book}}: |journal= ignored (help)
18. Grandin, R.; Socquet, A.; Binet, R.; Klinger, Y.; Jacques, E.; Chabalier, J.-B. de; King, G. C. P.; Lasserre, C.; Tait, S. (2009-08-01). "September 2005 Manda Hararo-Dabbahu rifting event, Afar (Ethiopia): Constraints provided by geodetic data" (PDF). Journal of Geophysical Research. 114 (B8): B08404. Bibcode:2009JGRB..114.8404G. doi:10.1029/2008jb005843. hdl:10220/8648. ISSN 2156-2202.
19. Burke, K (1977-05-01). "Aulacogens and Continental Breakup". Annual Review of Earth and Planetary Sciences. 5 (1): 371–396. Bibcode:1977AREPS...5..371B. doi:10.1146/annurev.ea.05.050177.002103. ISSN 0084-6597.
20. DeMets, Charles; Gordon, Richard G.; Argus, Donald F. (2010). "Geologically current plate motions". Geophysical Journal International. 181 (1): 52. Bibcode:2010GeoJI.181....1D. doi:10.1111/j.1365-246X.2009.04491.x.
21. Bhagwat, S.B. (2009). Foundation of Geology Vol 1. Global Vision Publishing House. p. 83. ISBN 9788182202764.
22. Elsasser, Walter M. (1971-02-10). "Sea-floor spreading as thermal convection". Journal of Geophysical Research. 76 (5): 1101–1112. Bibcode:1971JGR....76.1101E. doi:10.1029/JB076i005p01101.
23. Patriat, Philippe; Achache, José (1984). "India–Eurasia collision chronology has implications for crustal shortening and driving mechanism of plates". Nature. 311 (5987): 615. Bibcode:1984Natur.311..615P. doi:10.1038/311615a0. S2CID 4315858.
24. McKenzie, Dan P. (1967-12-15). "Some remarks on heat flow and gravity anomalies". Journal of Geophysical Research. 72 (24): 6261–6273. Bibcode:1967JGR....72.6261M. doi:10.1029/JZ072i024p06261.
25. Sclater, J. G.; Francheteau, J. (1970-09-01). "The Implications of Terrestrial Heat Flow Observations on Current Tectonic and Geochemical Models of the Crust and Upper Mantle of the Earth". Geophysical Journal International. 20 (5): 509–542. Bibcode:1970GeoJ...20..509S. doi:10.1111/j.1365-246X.1970.tb06089.x. ISSN 0956-540X.
26. Sclater, John G.; Anderson, Roger N.; Bell, M. Lee (1971-11-10). "Elevation of ridges and evolution of the central eastern Pacific". Journal of Geophysical Research. 76 (32): 7888–7915. Bibcode:1971JGR....76.7888S. doi:10.1029/jb076i032p07888. ISSN 2156-2202.
27. ^ Parsons, Barry; Sclater, John G. (1977-02-10). "An analysis of the variation of ocean floor bathymetry and heat flow with age". Journal of Geophysical Research. 82 (5): 803–827. Bibcode:1977JGR....82..803P. doi:10.1029/jb082i005p00803. ISSN 2156-2202.
28. ^ Davis, E.E; Lister, C. R. B. (1974). "Fundamentals of Ridge Crest Topography". Earth and Planetary Science Letters. 21 (4): 405–413. Bibcode:1974E&PSL..21..405D. doi:10.1016/0012-821X(74)90180-0.

External links

• Animation of a mid-ocean ridge

v t e Physical oceanography
Waves	Airy wave theory Ballantine scale Benjamin–Feir instability Boussinesq approximation Breaking wave Clapotis Cnoidal wave Cross sea Dispersion Edge wave Equatorial waves Gravity wave Green's law Infragravity wave Internal wave Iribarren number Kelvin wave Kinematic wave Longshore drift Luke's variational principle Mild-slope equation Radiation stress Rogue wave Rossby wave Rossby-gravity waves Sea state Seiche Significant wave height Soliton Stokes drift Stokes problem Stokes wave Swell Trochoidal wave Tsunami megatsunami Undertow Ursell number Wave action Wave base Wave height Wave nonlinearity Wave power Wave radar Wave setup Wave shoaling Wave turbulence Wave–current interaction Waves and shallow water one-dimensional Saint-Venant equations shallow water equations Wind fetch Wind setup Wind wave model
Circulation	Atmospheric circulation Baroclinity Boundary current Coriolis force Coriolis–Stokes force Craik–Leibovich vortex force Downwelling Eddy Ekman layer Ekman spiral Ekman transport El Niño–Southern Oscillation General circulation model Geochemical Ocean Sections Study Geostrophic current Global Ocean Data Analysis Project Gulf Stream Humboldt Current Hydrothermal circulation Langmuir circulation Longshore drift Loop Current Modular Ocean Model Ocean current Ocean dynamical thermostat Ocean dynamics Ocean gyre Overflow Princeton Ocean Model Rip current Subsurface ocean current Sverdrup balance Thermohaline circulation shutdown Upwelling Whirlpool Wind generated current World Ocean Circulation Experiment
Tides	Amphidromic point Earth tide Head of tide Internal tide Lunitidal interval Perigean spring tide Rip tide Rule of twelfths Slack tide Theory of tides Tidal bore Tidal force Tidal power Tidal race Tidal range Tidal resonance Tide gauge Tideline
Landforms	Abyssal fan Abyssal plain Atoll Bathymetric chart Carbonate platform Coastal geography Cold seep Continental margin Continental rise Continental shelf Contourite Guyot Hydrography Knoll Ocean bank Oceanic basin Oceanic plateau Oceanic trench Passive margin Seabed Seamount Submarine canyon Submarine volcano
Plate tectonics	Convergent boundary Divergent boundary Fracture zone Hydrothermal vent Marine geology Mid-ocean ridge Mohorovičić discontinuity Oceanic crust Outer trench swell Ridge push Seafloor spreading Slab pull Slab suction Slab window Subduction Transform fault Vine–Matthews–Morley hypothesis Volcanic arc
Ocean zones	Benthic Deep ocean water Deep sea Littoral Mesopelagic Oceanic Pelagic Photic Surf Swash
Sea level	Deep-ocean Assessment and Reporting of Tsunamis Global Sea Level Observing System North West Shelf Operational Oceanographic System Sea-level curve Sea level drop Sea level rise World Geodetic System
Acoustics	Deep scattering layer Ocean acoustic tomography Sofar bomb SOFAR channel Underwater acoustics
Satellites	Jason-1 OSTM/Jason-2 Jason-3
Related	Acidification Argo Benthic lander Color of water DSV Alvin Marginal sea Marine energy Marine pollution Mooring National Oceanographic Data Center Ocean Explorations Observations Reanalysis Ocean surface topography Ocean temperature Ocean thermal energy conversion Oceanography Outline of oceanography Pelagic sediment Sea surface microlayer Sea surface temperature Seawater Science On a Sphere Stratification Thermocline Underwater glider Water column World Ocean Atlas
Category Commons Oceans portal

• Geological processes
• Plate tectonics
• Oceanographical terminology