In mathematics, a heteroclinic cycle is an invariant set in the phase space of a dynamical system. It is a topological circle of equilibrium points and connecting heteroclinic orbits. If a heteroclinic cycle is asymptotically stable, approaching trajectories spend longer and longer periods of time in a neighbourhood of successive equilibria.
In generic dynamical systems heteroclinic connections are of high co-dimension, that is, they will not persist if parameters are varied.
Robust heteroclinic cycles
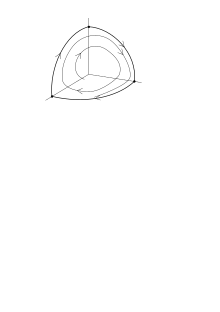
A robust heteroclinic cycle is one which persists under small changes in the underlying dynamical system. Robust cycles often arise in the presence of symmetry or other constraints which force the existence of invariant hyperplanes. A prototypical example of a robust heteroclinic cycle is the Guckenheimer–Holmes cycle. This cycle has also been studied in the context of rotating convection, and as three competing species in population dynamics.
See also
References
- Guckenheimer, John; Holmes, Philip (1988). "Structurally Stable Heteroclinic Cycles". Mathematical Proceedings of the Cambridge Philosophical Society. 103 (1): 189–192. doi:10.1017/S0305004100064732.
- Busse, F. M.; Heikes, K. E. (1980). "Convection in a rotating layer: A simple case of turbulence". Science. 208: 173–175. doi:10.1126/science.208.4440.173.
- May, Robert M.; Leonard, Warren J. (1975). "Nonlinear aspects of competition between three species". SIAM Journal on Applied Mathematics. 29 (2): 243–253. doi:10.1137/0129022.