 7-simplex |
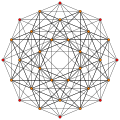 Hexicated 7-simplex |
 Hexitruncated 7-simplex |
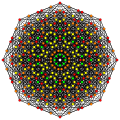 Hexicantellated 7-simplex |
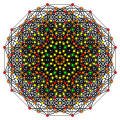 Hexiruncinated 7-simplex |
 Hexicantitruncated 7-simplex |
 Hexiruncitruncated 7-simplex |
 Hexiruncicantellated 7-simplex |
 Hexisteritruncated 7-simplex |
 Hexistericantellated 7-simplex |
 Hexipentitruncated 7-simplex |
 Hexiruncicantitruncated 7-simplex |
 Hexistericantitruncated 7-simplex |
 Hexisteriruncitruncated 7-simplex |
 Hexisteriruncicantellated 7-simplex |
 Hexipenticantitruncated 7-simplex |
 Hexipentiruncitruncated 7-simplex |
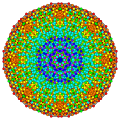 Hexisteriruncicantitruncated 7-simplex |
 Hexipentiruncicantitruncated 7-simplex |
 Hexipentistericantitruncated 7-simplex |
 Hexipentisteriruncicantitruncated 7-simplex (Omnitruncated 7-simplex) | |||
| Orthogonal projections in A7 Coxeter plane | |||
|---|---|---|---|
In seven-dimensional geometry, a hexicated 7-simplex is a convex uniform 7-polytope, including 6th-order truncations (hexication) from the regular 7-simplex.
There are 20 unique hexications for the 7-simplex, including all permutations of truncations, cantellations, runcinations, sterications, and pentellations.
The simple hexicated 7-simplex is also called an expanded 7-simplex, with only the first and last nodes ringed, is constructed by an expansion operation applied to the regular 7-simplex. The highest form, the hexipentisteriruncicantitruncated 7-simplex is more simply called a omnitruncated 7-simplex with all of the nodes ringed.
Hexicated 7-simplex
| Hexicated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | 254: 8+8 {3} 28+28 {}x{3} 56+56 {3}x{3,3,3} 70 {3,3}x{3,3} |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 336 |
| Vertices | 56 |
| Vertex figure | 5-simplex antiprism |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
In seven-dimensional geometry, a hexicated 7-simplex is a convex uniform 7-polytope, a hexication (6th order truncation) of the regular 7-simplex, or alternately can be seen as an expansion operation.

Root vectors
Its 56 vertices represent the root vectors of the simple Lie group A7.
Alternate names
- Expanded 7-simplex
- Small petated hexadecaexon (acronym: suph) (Jonathan Bowers)
Coordinates
The vertices of the hexicated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,1,1,1,2). This construction is based on facets of the hexicated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
A second construction in 8-space, from the center of a rectified 8-orthoplex is given by coordinate permutations of:
- (1,-1,0,0,0,0,0,0)
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|
|
|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexitruncated 7-simplex
| hexitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 1848 |
| Vertices | 336 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petitruncated octaexon (acronym: puto) (Jonathan Bowers)
Coordinates
The vertices of the hexitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,1,1,2,3). This construction is based on facets of the hexitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|
|
| Dihedral symmetry |
Hexicantellated 7-simplex
| Hexicantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 5880 |
| Vertices | 840 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petirhombated octaexon (acronym: puro) (Jonathan Bowers)
Coordinates
The vertices of the hexicantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,1,2,2,3). This construction is based on facets of the hexicantellated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|
|
| Dihedral symmetry |
Hexiruncinated 7-simplex
| Hexiruncinated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,3,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 8400 |
| Vertices | 1120 |
| Vertex figure | |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
Alternate names
- Petiprismated hexadecaexon (acronym: puph) (Jonathan Bowers)
Coordinates
The vertices of the hexiruncinated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,2,2,2,3). This construction is based on facets of the hexiruncinated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|
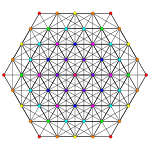
|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|

|
| Dihedral symmetry | ] | ] |
Hexicantitruncated 7-simplex
| Hexicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 8400 |
| Vertices | 1680 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petigreatorhombated octaexon (acronym: pugro) (Jonathan Bowers)
Coordinates
The vertices of the hexicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,1,2,3,4). This construction is based on facets of the hexicantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
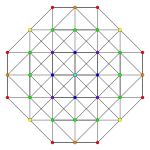
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|
|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry |
Hexiruncitruncated 7-simplex
| Hexiruncitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 20160 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petiprismatotruncated octaexon (acronym: pupato) (Jonathan Bowers)
Coordinates
The vertices of the hexiruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,2,2,3,4). This construction is based on facets of the hexiruncitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry |
Hexiruncicantellated 7-simplex
| Hexiruncicantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,3,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 16800 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
In seven-dimensional geometry, a hexiruncicantellated 7-simplex is a uniform 7-polytope.
Alternate names
- Petiprismatorhombated octaexon (acronym: pupro) (Jonathan Bowers)
Coordinates
The vertices of the hexiruncicantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,1,2,3,3,4). This construction is based on facets of the hexiruncicantellated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|
|
| Dihedral symmetry |
Hexisteritruncated 7-simplex
| hexisteritruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,4,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 20160 |
| Vertices | 3360 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Peticellitruncated octaexon (acronym: pucto) (Jonathan Bowers)
Coordinates
The vertices of the hexisteritruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,2,2,3,4). This construction is based on facets of the hexisteritruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|
|
| Dihedral symmetry |
Hexistericantellated 7-simplex
| hexistericantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,4,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | t0,2,4{3,3,3,3,3} {}xt0,2,4{3,3,3,3} |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 30240 |
| Vertices | 5040 |
| Vertex figure | |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
Alternate names
- Peticellirhombihexadecaexon (acronym: pucroh) (Jonathan Bowers)
Coordinates
The vertices of the hexistericantellated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,2,3,3,4). This construction is based on facets of the hexistericantellated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|
|
| Dihedral symmetry | ] | ] |
Hexipentitruncated 7-simplex
| Hexipentitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,5,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 8400 |
| Vertices | 1680 |
| Vertex figure | |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
Alternate names
- Petiteritruncated hexadecaexon (acronym: putath) (Jonathan Bowers)
Coordinates
The vertices of the hexipentitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,2,2,2,2,3,4). This construction is based on facets of the hexipentitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexiruncicantitruncated 7-simplex
| Hexiruncicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 30240 |
| Vertices | 6720 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petigreatoprismated octaexon (acronym: pugopo) (Jonathan Bowers)
Coordinates
The vertices of the hexiruncicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,2,3,4,5). This construction is based on facets of the hexiruncicantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexistericantitruncated 7-simplex
| Hexistericantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,4,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 50400 |
| Vertices | 10080 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Peticelligreatorhombated octaexon (acronym: pucagro) (Jonathan Bowers)
Coordinates
The vertices of the hexistericantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,2,3,4,5). This construction is based on facets of the hexistericantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexisteriruncitruncated 7-simplex
| Hexisteriruncitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3,4,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 45360 |
| Vertices | 10080 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Peticelliprismatotruncated octaexon (acronym: pucpato) (Jonathan Bowers)
Coordinates
The vertices of the hexisteriruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,3,3,4,5). This construction is based on facets of the hexisteriruncitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|
|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry |
Hexisteriruncicantellated 7-simplex
| Hexisteriruncicantellated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2,3,4,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 45360 |
| Vertices | 10080 |
| Vertex figure | |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
Alternate names
- Peticelliprismatorhombihexadecaexon (acronym: pucproh) (Jonathan Bowers)
Coordinates
The vertices of the hexisteriruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,3,4,4,5). This construction is based on facets of the hexisteriruncitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexipenticantitruncated 7-simplex
| hexipenticantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,5,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 30240 |
| Vertices | 6720 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petiterigreatorhombated octaexon (acronym: putagro) (Jonathan Bowers)
Coordinates
The vertices of the hexipenticantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,2,2,2,3,4,5). This construction is based on facets of the hexipenticantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | |||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry |
Hexipentiruncitruncated 7-simplex
| Hexipentiruncitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,3,5,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | |
| Vertices | 10080 |
| Vertex figure | |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
Alternate names
- Petiteriprismatotruncated hexadecaexon (acronym: putpath) (Jonathan Bowers)
Coordinates
The vertices of the hexipentiruncitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,2,2,3,4,4,5). This construction is based on facets of the hexipentiruncitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|

|
| Dihedral symmetry | ] | ] |
Hexisteriruncicantitruncated 7-simplex
| Hexisteriruncicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,4,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 80640 |
| Vertices | 20160 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petigreatocellated octaexon (acronym: pugaco) (Jonathan Bowers)
Coordinates
The vertices of the hexisteriruncicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,1,2,3,4,5,6). This construction is based on facets of the hexisteriruncicantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexipentiruncicantitruncated 7-simplex
| Hexipentiruncicantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,5,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 80640 |
| Vertices | 20160 |
| Vertex figure | |
| Coxeter group | A7, , order 40320 |
| Properties | convex |
Alternate names
- Petiterigreatoprismated octaexon (acronym: putgapo) (Jonathan Bowers)
Coordinates
The vertices of the hexipentiruncicantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,2,2,3,4,5,6). This construction is based on facets of the hexipentiruncicantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Hexipentistericantitruncated 7-simplex
| Hexipentistericantitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,4,5,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | |
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 80640 |
| Vertices | 20160 |
| Vertex figure | |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
Alternate names
- Petitericelligreatorhombihexadecaexon (acronym: putcagroh) (Jonathan Bowers)
Coordinates
The vertices of the hexipentistericantitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,2,3,3,4,5,6). This construction is based on facets of the hexipentistericantitruncated 8-orthoplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|

|

|
| Dihedral symmetry | ] | ] |
Omnitruncated 7-simplex
| Omnitruncated 7-simplex | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2,3,4,5,6{3} |
| Coxeter-Dynkin diagrams | |
| 6-faces | 254 |
| 5-faces | 5796 |
| 4-faces | 40824 |
| Cells | 126000 |
| Faces | 191520 |
| Edges | 141120 |
| Vertices | 40320 |
| Vertex figure | Irr. 6-simplex |
| Coxeter group | A7×2, ], order 80640 |
| Properties | convex |
The omnitruncated 7-simplex is composed of 40320 (8 factorial) vertices and is the largest uniform 7-polytope in the A7 symmetry of the regular 7-simplex. It can also be called the hexipentisteriruncicantitruncated 7-simplex which is the long name for the omnitruncation for 7 dimensions, with all reflective mirrors active.
Permutohedron and related tessellation
The omnitruncated 7-simplex is the permutohedron of order 8. The omnitruncated 7-simplex is a zonotope, the Minkowski sum of eight line segments parallel to the eight lines through the origin and the eight vertices of the 7-simplex.
Like all uniform omnitruncated n-simplices, the omnitruncated 7-simplex can tessellate space by itself, in this case 7-dimensional space with three facets around each ridge. It has Coxeter-Dynkin diagram of ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Alternate names
- Great petated hexadecaexon (Acronym: guph) (Jonathan Bowers)
Coordinates
The vertices of the omnitruncated 7-simplex can be most simply positioned in 8-space as permutations of (0,1,2,3,4,5,6,7). This construction is based on facets of the hexipentisteriruncicantitruncated 8-orthoplex, t0,1,2,3,4,5,6{3,4}, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Images
| Ak Coxeter plane | A7 | A6 | A5 |
|---|---|---|---|
| Graph | 
|

|

|
| Dihedral symmetry | ] | ||
| Ak Coxeter plane | A4 | A3 | A2 |
| Graph | 
|
|
|
| Dihedral symmetry | ] | ] |
Related polytopes
These polytope are a part of 71 uniform 7-polytopes with A7 symmetry.
Notes
- Klitzing, (x3o3o3o3o3o3x - suph)
- Klitzing, (x3x3o3o3o3o3x- puto)
- Klitzing, (x3o3x3o3o3o3x - puro)
- Klitzing, (x3o3o3x3o3o3x - puph)
- Klitzing, (x3o3o3o3x3o3x - pugro)
- Klitzing, (x3x3x3o3o3o3x - pupato)
- Klitzing, (x3o3x3x3o3o3x - pupro)
- Klitzing, (x3x3o3o3x3o3x - pucto)
- Klitzing, (x3o3x3o3x3o3x - pucroh)
- Klitzing, (x3x3o3o3o3x3x - putath)
- Klitzing, (x3x3x3x3o3o3x - pugopo)
- Klitzing, (x3x3x3o3x3o3x - pucagro)
- Klitzing, (x3x3o3x3x3o3x - pucpato)
- Klitzing, (x3o3x3x3x3o3x - pucproh)
- Klitzing, (x3x3x3o3o3x3x - putagro)
- Klitzing, (x3x3o3x3o3x3x - putpath)
- Klitzing, (x3x3x3x3x3o3x - pugaco)
- Klitzing, (x3x3x3x3o3x3x - putgapo)
- Klitzing, (x3x3x3o3x3x3x - putcagroh)
- Klitzing, (x3x3x3x3x3x3x - guph)
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6, wiley.com
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I,
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II,
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III,
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, PhD (1966)
- Klitzing, Richard. "7D". x3o3o3o3o3o3x - suph, x3x3o3o3o3o3x- puto, x3o3x3o3o3o3x - puro, x3o3o3x3o3o3x - puph, x3o3o3o3x3o3x - pugro, x3x3x3o3o3o3x - pupato, x3o3x3x3o3o3x - pupro, x3x3o3o3x3o3x - pucto, x3o3x3o3x3o3x - pucroh, x3x3o3o3o3x3x - putath, x3x3x3x3o3o3x - pugopo, x3x3x3o3x3o3x - pucagro, x3x3o3x3x3o3x - pucpato, x3o3x3x3x3o3x - pucproh, x3x3x3o3o3x3x - putagro, x3x3x3x3o3x3x - putpath, x3x3x3x3x3o3x - pugaco, x3x3x3x3o3x3x - putgapo, x3x3x3o3x3x3x - putcagroh, x3x3x3x3x3x3x - guph
External links
| Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||