Misplaced Pages

HydroGeoSphere

Developer(s)	Aquanty
Stable release	2023
Operating system	Windows, Linux
Type	Hydrogeology software
License	Proprietary
Website	www.aquanty.com/hydrogeosphere/

HydroGeoSphere (HGS) is a 3D control-volume finite element groundwater model, and is based on a rigorous conceptualization of the hydrologic system consisting of surface and subsurface flow regimes. The model is designed to take into account all key components of the hydrologic cycle. For each time step, the model solves surface and subsurface flow, solute and energy transport equations simultaneously, and provides a complete water and solute balance.

History

The original name for the code was FRAC3DVS, which was created by René Therrien in 1992. The code was further developed jointly at the University of Waterloo and the Laval University, and was primarily used for academic research. It was renamed to HydroGeoSphere in 2002 with the implementation of 2D surface water flow and transport. In 2012, the software became commercialized under the support and management of Aquanty Inc.

Governing equations

In order to accomplish the integrated analysis, HydroGeoSphere utilizes a rigorous, mass conservative modeling approach that fully couples the surface flow and transport equations with the 3-D, variably saturated subsurface flow and transport equations. This approach is significantly more robust than previous conjunctive approaches that rely on linkage of separate surface and subsurface modeling codes.

Groundwater Flow

HydroGeoSphere assumes that the subsurface flow equation in a porous medium is always solved during a simulation, either for fully saturated or variably saturated flow conditions. The subsurface flow equation can be expanded to incorporate discrete fractures, a second interacting porous continuum, wells, tile drains and surface flow. The following assumptions are made for subsurface flow:

• The fluid is essentially incompressible.
• The porous medium and fractures (or macropores), if present, are non-deformable.
• The system is under isothermal conditions.
• The air phase is infinitely mobile.

The Richards’ equation is used to describe three-dimensional transient subsurface flow in a variably saturated porous medium:

${\displaystyle -\nabla \cdot (w_{m}{\textbf {q}})+\sum \Gamma _{eq}\pm Q=w_{m}{\frac {\partial }{\partial t}}(\theta _{s}S_{w})}$

The fluid flux, ${\displaystyle {\textbf {q}}}$, is represented by the Darcy's law shown as:

${\displaystyle {\textbf {q}}=-{\textbf {K}}\cdot k_{r}\nabla (\psi +z)}$

where ${\displaystyle w_{m}}$ is the volumetric fraction of the total porosity occupied by the porous medium, ${\displaystyle \Gamma _{ex}}$ is the internal fluid exchange rate (e.g. surface water, wells, and tile drains), ${\displaystyle Q}$ is the external fluid outside of the model domain, ${\displaystyle \theta _{s}}$ is the saturated water content, ${\displaystyle S_{w}}$ is the degree of saturation, ${\displaystyle {\textbf {K}}}$ is the hydraulic conductivity tensor, ${\displaystyle k_{r}}$ is the relative permeability of the medium calculated as a function of saturation, ${\displaystyle \psi }$ is the pressure head, and ${\displaystyle z}$ is the elevation head.

Surface water flow

Areal surface water flow is represented in HydroGeoSphere by a two-dimensional depth-averaged flow equation, which is the diffusion-wave approximation of the Saint Venant equation for surface water flow. HydroGeoSphere's surface water flow component is implemented with the following assumptions:

• Depth-averaged flow velocities
• Hydrostatic pressure distribution vertically
• Mild slope
• Dominant bottom shear stresses.

The surface flow components are solved by the following three equations, which are given by the following mass balance equation:

${\displaystyle {\frac {\partial \phi _{o}h_{o}}{\partial t}}+{\frac {\partial {\bar {v}}_{xo}d_{o}}{\partial x}}+{\frac {\partial {\bar {v}}_{yo}d_{o}}{\partial y}}+d_{o}\Gamma _{o}\pm Q_{o}=0}$

coupled with the momentum equations, neglecting inertia terms, for the x-direction:

${\displaystyle {\bar {v}}_{ox}=-K_{ox}{\frac {\partial h_{o}}{\partial x}}}$

and for the y-direction:

${\displaystyle {\bar {v}}_{oy}=-K_{oy}{\frac {\partial h_{o}}{\partial y}}}$

where ${\displaystyle \phi _{o}}$ is the surface flow domain porosity, ${\displaystyle h_{o}}$ is the water surface elevation, ${\displaystyle {\bar {v}}_{xo}}$ and ${\displaystyle {\bar {v}}_{yo}}$ are the vertically averaged flow velocities in the x and y directions, ${\displaystyle d_{o}}$ is the depth of surface water flow, ${\displaystyle \Gamma _{o}}$ is the internal fluid exchange, and ${\displaystyle Q_{o}}$ is the external fluid exchange. The surface conductances, ${\displaystyle K_{ox}}$ and ${\displaystyle K_{oy}}$ are approximated by either the Manning or Chezy equation.

Solute transport

Three-dimensional transport of solutes is described by the modified reactive transport advective-dispersion equation:

${\displaystyle -\nabla \cdot w_{m}({\textbf {q}}C-\theta _{s}S_{w}{\textbf {D}}\nabla C)+_{par}+\sum {\Omega _{ex}+Q_{c}}=w_{m}\left}$

where ${\displaystyle C}$ is the solute concentration, ${\displaystyle \lambda }$ is the first-order decay constant, ${\displaystyle Q_{c}}$ is the external source or sink term, ${\displaystyle \Omega }$ is the internal solute transfer between domains, ${\displaystyle R}$ is the retardation factor, ${\displaystyle {\textbf {D}}}$ is the diffusion coefficient, and ${\displaystyle par}$ designates parent species for the case of a decay chain.

Heat transport

Graf incorporated heat transport within the saturated-zone flow regime into HydroGeoSphere together with temperature-dependent fluid properties, such as viscosity and density. The model’s capability was successfully demonstrated for the case of thermohaline flow and transport in porous and fractured porous media . This work extends the model’s capability to include thermal energy transport in the unsaturated zone and in the surface water, which is considered a key step in the linkage between the atmospheric and hydrologic systems. Surface heat fluxes from atmospheric inputs are an important source/sink of thermal energy, especially to the surface water system. As such, surface heat fluxes across the land surface were also incorporated into HydroGeoSphere. A complete description of the physical processes and governing flow and solute transport equations that form the basis of HydroGeoSphere can be found in Therrien et al. and therefore will not be presented here.

The general equation for variably saturated subsurface thermal energy transport following Molson et al. is given by:

${\displaystyle -\nabla \cdot {\Big (}{\textbf {q}}\rho _{w}c_{w}T-(k_{b}+c_{b}\rho _{b}{\textbf {D}})\nabla T{\Big )}+\Omega _{o}\pm Q_{T}={\frac {\partial \rho _{b}c_{b}T}{\partial t}}}$

where ${\displaystyle \rho }$ is the density, ${\displaystyle c}$ is the heat capacity, ${\displaystyle T}$ is the temperature of the bulk subsurface, ${\displaystyle k}$ is the thermal conductivity, ${\displaystyle D}$ is the thermal dispersion term, ${\displaystyle Q_{T}}$ is the thermal source/sink, ${\displaystyle \Omega _{o}}$ is the thermal interactions between the surface and subsurface, and ${\displaystyle Q_{T}}$ is the external thermal interactions.

Surface-subsurface coupling

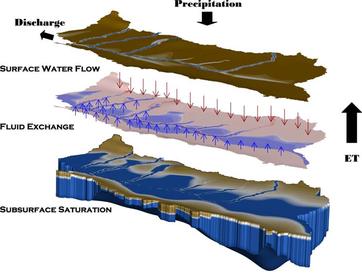
The 2-D areal surface flow modules of HydroGeoSphere follow the same conventions for spatial and temporal discretizations as those used by the subsurface modules. The surface flow equation is solved on a 2-D finite-element mesh stacked upon a subsurface grid when solving for both domains (i.e. the x- and y-locations of nodes are the same for each layer of nodes). For superposition, the grid generated for the subsurface domain is mirrored areally for the surface flow nodes, with surface flow node elevations corresponding to the top elevation of the topmost active layer of the subsurface grid. Note that surface flow node elevations may vary substantially to conform with topography. However, the assumptions of small slope inherent in the diffusion-wave equation will not allow for modeling of inertial effects.

The discretized surface equation is coupled with the 3-D subsurface flow equation via superposition (common node approach) or via leakage through a surficial skin layer (dual node approach). For both approaches, fully implicit coupling of the surface and subsurface flow regimes provides an integral view of the movement of water, as opposed to the traditional division of surface and subsurface regimes. Flux across the land surface is, therefore, a natural internal process allowing water to move between the surface and subsurface flow systems as governed by local flow hydrodynamics, instead of using physically artificial boundary conditions at the interface. When the subsurface connection is provided via superposition, HydroGeoSphere adds the surface flow equation terms for the 2-D surface mesh to those of the top layer of subsurface nodes. In that case, the fluid exchange flux, which contains leakance term does not need to be explicitly defined.

Features

The HGS model is a three-dimensional control-volume finite element simulator which is designed to simulate the entire terrestrial portion of the hydrologic cycle. It uses a globally implicit approach to simultaneously solve the 2D diffusive-wave equation and the 3D form of Richards’ equation. HGS also dynamically integrates key components of the hydrologic cycle such as evaporation from bare soil and water bodies, vegetation-dependent transpiration with root uptake, snowmelt and soil freeze/thaw. Features such as macro pores, fractures, and tile drains can either be incorporated discretely or using a dual-porosity, dual permeability formulation. Additionally, HydroGeoSphere has been linked to Weather Research and Forecasting, a mesoscale atmospheric model for fully coupled subsurface, surface, and atmospheric simulations.

Other groundwater models

• FEFLOW
• MODFLOW
• OpenGeoSys

References

1. Therrien, R.; Sudicky, E.A. (1996). "Three-dimensional analysis of variably-saturated flow and solute transport in discretely-fractured porous media". Journal of Contaminant Hydrology. 23 (1–2): 1–44. Bibcode:1996JCHyd..23....1T. doi:10.1016/0169-7722(95)00088-7.
2. ^ Brunner, Philip; Simmons, Craig T. (2012). "HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model". Groundwater. 50 (2): 170–176. Bibcode:2012GrWat..50..170B. doi:10.1111/j.1745-6584.2011.00882.x. S2CID 54822458.
3. Therrien, René (1992). Three-dimensional analysis of variably saturated flow and solute transport in discretely-fractured porous media (Ph.D.). University of Waterloo, Waterloo, Ontario.
4. Davison, Jason Hamilton; Hwang, Hyoun-Tae; Sudicky, Edward A.; Mallia, Derek V.; Lin, John C. (2018). "Full Coupling Between the Atmosphere, Surface, and Subsurface for Integrated Hydrologic Simulation". Journal of Advances in Modeling Earth Systems. 10 (1): 43–53. Bibcode:2018JAMES..10...43D. doi:10.1002/2017ms001052. ISSN 1942-2466.

External links

• Official website

• Scientific simulation software
• Hydrogeology software
• Hydrology models
• Integrated hydrologic modelling
• Earth sciences software