 | This article may be too technical for most readers to understand. Please help improve it to make it understandable to non-experts, without removing the technical details. (July 2013) (Learn how and when to remove this message) |
| Order-4 apeirogonal tiling | |
|---|---|
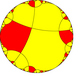
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | ∞ |
| Schläfli symbol | {∞,4} r{∞,∞} t(∞,∞,∞) t0,1,2,3(∞,∞,∞,∞) |
| Wythoff symbol | 4 | ∞ 2 2 | ∞ ∞ ∞ ∞ | ∞ |
| Coxeter diagram |       
|
| Symmetry group | , (*∞42) , (*∞∞2) , (*∞∞∞) (*∞∞∞∞) |
| Dual | Infinite-order square tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive edge-transitive |
In geometry, the order-4 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,4}.
Symmetry
This tiling represents the mirror lines of *2 symmetry. Its dual tiling represents the fundamental domains of orbifold notation *∞∞∞∞ symmetry, a square domain with four ideal vertices.
Uniform colorings
Like the Euclidean square tiling there are 9 uniform colorings for this tiling, with 3 uniform colorings generated by triangle reflective domains. A fourth can be constructed from an infinite square symmetry (*∞∞∞∞) with 4 colors around a vertex. The checker board, r{∞,∞}, coloring defines the fundamental domains of , (*∞44) symmetry, usually shown as black and white domains of reflective orientations.
| 1 color | 2 color | 3 and 2 colors | 4, 3 and 2 colors | |||
|---|---|---|---|---|---|---|
| , (*∞42) | , (*∞∞2) | , (*∞∞∞) | (*∞∞∞∞) | |||
| {∞,4} | r{∞,∞} = {∞,4}1⁄2 |
t0,2(∞,∞,∞) = r{∞,∞}1⁄2 |
t0,1,2,3(∞,∞,∞,∞) = r{∞,∞}1⁄4 = {∞,4}1⁄8 | |||
(1111) |
 (1212) |
 (1213) |
 (1112) |
 (1234) |
 (1123) |
 (1122) |
|
|
  = 
|
= = 
|
 =  =
| |||
Related polyhedra and tiling
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,4}, and Coxeter diagram 
, with n progressing to infinity.
| *n42 symmetry mutation of regular tilings: {n,4} | |||||||
|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | |||||
|
|
|
|
|
|
|
|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | ...∞ |
| Paracompact uniform tilings in family | |||||||
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
| {∞,4} | t{∞,4} | r{∞,4} | 2t{∞,4}=t{4,∞} | 2r{∞,4}={4,∞} | rr{∞,4} | tr{∞,4} | |
| Dual figures | |||||||
|
|
|
|
|
|
| |
|
|
|
|
|
|
| |
| V∞ | V4.∞.∞ | V(4.∞) | V8.8.∞ | V4 | V4.∞ | V4.8.∞ | |
| Alternations | |||||||
(*44∞) |
(∞*2) |
(*2∞2∞) |
(4*∞) |
(*∞∞2) |
(2*2∞) |
(∞42) | |
 =  
|
|
|
|
= 
|
|
| |
| h{∞,4} | s{∞,4} | hr{∞,4} | s{4,∞} | h{4,∞} | hrr{∞,4} | s{∞,4} | |
|
|
|
| ||||
| Alternation duals | |||||||
|
|
|
|
|
|
| |
|
|
||||||
| V(∞.4) | V3.(3.∞) | V(4.∞.4) | V3.∞.(3.4) | V∞ | V∞.4 | V3.3.4.3.∞ | |
| Paracompact uniform tilings in family | ||||||
|---|---|---|---|---|---|---|
= = 
|
= =
|
= =
|
= =
|
= =
|
=
|
=
|
|
|
|
|
|
|
|
|
| {∞,∞} | t{∞,∞} | r{∞,∞} | 2t{∞,∞}=t{∞,∞} | 2r{∞,∞}={∞,∞} | rr{∞,∞} | tr{∞,∞} |
| Dual tilings | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| V∞ | V∞.∞.∞ | V(∞.∞) | V∞.∞.∞ | V∞ | V4.∞.4.∞ | V4.4.∞ |
| Alternations | ||||||
(*∞∞2) |
(∞*∞) |
(*∞∞∞∞) |
(∞*∞) |
(*∞∞2) |
(2*∞∞) |
(2∞∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
| h{∞,∞} | s{∞,∞} | hr{∞,∞} | s{∞,∞} | h2{∞,∞} | hrr{∞,∞} | sr{∞,∞} |
| Alternation duals | ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| |||
| V(∞.∞) | V(3.∞) | V(∞.4) | V(3.∞) | V∞ | V(4.∞.4) | V3.3.∞.3.∞ |
| Paracompact uniform tilings in family | ||||||
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| (∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) h2{∞,∞} |
(∞,∞,∞) h{∞,∞} |
r(∞,∞,∞) r{∞,∞} |
t(∞,∞,∞) t{∞,∞} |
| Dual tilings | ||||||
|
|
|
|
|
|
|
| V∞ | V∞.∞.∞.∞ | V∞ | V∞.∞.∞.∞ | V∞ | V∞.∞.∞.∞ | V∞.∞.∞ |
| Alternations | ||||||
(*∞∞∞∞) |
(∞*∞) |
(*∞∞∞∞) |
(∞*∞) |
(*∞∞∞∞) |
(∞*∞) |
(∞∞∞) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Alternation duals | ||||||
|
|
|
|
|
|
|
|
| V(∞.∞) | V(∞.4) | V(∞.∞) | V(∞.4) | V(∞.∞) | V(∞.4) | V3.∞.3.∞.3.∞ |
See also
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
| Tessellation | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|   | ||||||||||||
| |||||||||||||
| |||||||||||||
| |||||||||||||