Misplaced Pages

Iitaka dimension

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.

In algebraic geometry, the Iitaka dimension of a line bundle L on an algebraic variety X is the dimension of the image of the rational map to projective space determined by L. This is 1 less than the dimension of the section ring of L

R ( X , L ) = ⨁ d = 0 ∞ H 0 ( X , L ⊗ d ) . {\displaystyle R(X,L)=\bigoplus _{d=0}^{\infty }H^{0}(X,L^{\otimes d}).}

The Iitaka dimension of L is always less than or equal to the dimension of X. If L is not effective, then its Iitaka dimension is usually defined to be − ∞ {\displaystyle -\infty } or simply said to be negative (some early references define it to be −1). The Iitaka dimension of L is sometimes called L-dimension, while the dimension of a divisor D is called D-dimension. The Iitaka dimension was introduced by Shigeru Iitaka (1970, 1971).

Big line bundles

A line bundle is big if it is of maximal Iitaka dimension, that is, if its Iitaka dimension is equal to the dimension of the underlying variety. Bigness is a birational invariant: If f : Y → X is a birational morphism of varieties, and if L is a big line bundle on X, then fL is a big line bundle on Y.

All ample line bundles are big.

Big line bundles need not determine birational isomorphisms of X with its image. For example, if C is a hyperelliptic curve (such as a curve of genus two), then its canonical bundle is big, but the rational map it determines is not a birational isomorphism. Instead, it is a two-to-one cover of the canonical curve of C, which is a rational normal curve.

Kodaira dimension

Main article: Kodaira dimension

The Iitaka dimension of the canonical bundle of a smooth variety is called its Kodaira dimension.

Iitaka conjecture

The m-pluricanonical map of complex manifolds M to W induces a fiber space structure.

Consider on complex algebraic varieties in the following.

Let K be the canonical bundle on M. The dimension of H(M,K), holomorphic sections of K, is denoted by Pm(M), called m-genus. Let

N ( M ) = { m ≥ 1 | P m ( M ) ≥ 1 } , {\displaystyle N(M)=\{m\geq 1|P_{m}(M)\geq 1\},}

then N(M) becomes to be all of the positive integer with non-zero m-genus. When N(M) is not empty, for m ∈ N ( M ) {\displaystyle m\in N(M)} m-pluricanonical map Φ m K {\displaystyle \Phi _{mK}} is defined as the map

Φ m K : M ⟶             P N z       ↦     ( φ 0 ( z ) : φ 1 ( z ) : ⋯ : φ N ( z ) ) {\displaystyle {\begin{aligned}\Phi _{mK}:&M\longrightarrow \ \ \ \ \ \ \mathbb {P} ^{N}\\&z\ \ \ \mapsto \ \ (\varphi _{0}(z):\varphi _{1}(z):\cdots :\varphi _{N}(z))\end{aligned}}}

where φ i {\displaystyle \varphi _{i}} are the bases of H(M,K). Then the image of Φ m K {\displaystyle \Phi _{mK}} , Φ m K ( M ) {\displaystyle \Phi _{mK}(M)} is defined as the submanifold of P N {\displaystyle \mathbb {P} ^{N}} .

For certain m {\displaystyle m} let Φ m k : M → W = Φ m K ( M ) ⊂ P N {\displaystyle \Phi _{mk}:M\rightarrow W=\Phi _{mK}(M)\subset \mathbb {P} ^{N}} be the m-pluricanonical map where W is the complex manifold embedded into projective space P.

In the case of surfaces with κ(M)=1 the above W is replaced by a curve C, which is an elliptic curve (κ(C)=0). We want to extend this fact to the general dimension and obtain the analytic fiber structure depicted in the upper right figure.

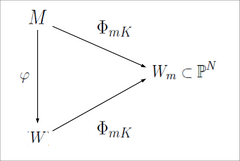
The m-pluricanonical map is birational invariant. Pm(M)=Pm(W)

Given a birational map φ : M ⟶ W {\displaystyle \varphi :M\longrightarrow W} , m-pluricanonical map brings the commutative diagram depicted in the left figure, which means that Φ m K ( M ) = Φ m K ( W ) {\displaystyle \Phi _{mK}(M)=\Phi _{mK}(W)} , i.e. m-pluricanonical genus is birationally invariant.

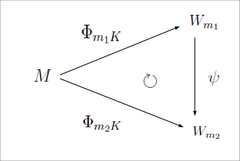
The existence of the birational map ψ : Wm1 → Wm2 in the projective space

It is shown by Iitaka that given n-dimensional compact complex manifold M with its Kodaira dimension κ(M) satisfying 1 ≤ κ(M) ≤ n-1, there are enough large m1,m2 such that Φ m 1 K : M ⟶ W m 1 ( M ) {\displaystyle \Phi _{m_{1}K}:M\longrightarrow W_{m_{1}}(M)} and Φ m 2 K : M ⟶ W m 2 ( M ) {\displaystyle \Phi _{m_{2}K}:M\longrightarrow W_{m_{2}}(M)} are birationally equivalent, which means there are the birational map φ : W m 1 ⟶ W m 2 ( M ) {\displaystyle \varphi :W_{m_{1}}\longrightarrow W_{m_{2}}(M)} . Namely, the diagram depicted in the right figure is commutative.

Furthermore, one can select M ∗ {\displaystyle M^{*}} that is birational with M {\displaystyle M} and W ∗ {\displaystyle W^{*}} that is birational with both W m 1 {\displaystyle W_{m_{1}}} and W m 1 {\displaystyle W_{m_{1}}} such that

Φ : M ∗ ⟶ W ∗ {\displaystyle \Phi :M^{*}\longrightarrow W^{*}}

is birational map, the fibers of Φ {\displaystyle \Phi } are simply connected and the general fibers of Φ {\displaystyle \Phi }

M w ∗ := Φ − 1 ( w ) ,     w ∈ W ∗ {\displaystyle M_{w}^{*}:=\Phi ^{-1}(w),\ \ w\in W^{*}}

have Kodaira dimension 0.

The above fiber structure is called the Iitaka fiber space. In the case of the surface S (n = 2 = dim(S)), W is the algebraic curve, the fiber structure is of dimension 1, and then the general fibers have the Kodaira dimension 0 i.e. elliptic curve. Therefore, S is the elliptic surface. These fact can be generalized to the general n. Therefore The study of the higher-dimensional birational geometry decompose to the part of κ=-∞,0,n and the fiber space whose fibers is of κ=0.

The following additional formula by Iitaka, called Iitaka conjecture, is important for the classification of algebraic varieties or compact complex manifolds.

Iitaka　Conjecture — Let f : V → W {\displaystyle f:V\rightarrow W} to be the fiber space from m-dimensional variety V {\displaystyle V} to n-dimensional variety W {\displaystyle W} and each fibers V w = f − 1 ( w ) {\displaystyle V_{w}=f^{-1}(w)} connected. Then

κ ( V ) ≥ κ ( V w ) + κ ( W ) . {\displaystyle \kappa (V)\geq \kappa (V_{w})+\kappa (W).}

This conjecture has been only partly solved, for example in the case of Moishezon manifolds. The classification theory might been said to be the effort to solve the Iitaka conjecture and lead another theorems that the three-dimensional variety V is abelian if and only if κ(V)=0 and q(V)=3 and its generalization so on. The minimal model program might be led from this conjecture.

References

Categories: