| This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (October 2023) (Learn how and when to remove this message) |

In electrical engineering, impedance matching is the practice of designing or adjusting the input impedance or output impedance of an electrical device for a desired value. Often, the desired value is selected to maximize power transfer or minimize signal reflection. For example, impedance matching typically is used to improve power transfer from a radio transmitter via the interconnecting transmission line to the antenna. Signals on a transmission line will be transmitted without reflections if the transmission line is terminated with a matching impedance.
Techniques of impedance matching include transformers, adjustable networks of lumped resistance, capacitance and inductance, or properly proportioned transmission lines. Practical impedance-matching devices will generally provide best results over a specified frequency band.
The concept of impedance matching is widespread in electrical engineering, but is relevant in other applications in which a form of energy, not necessarily electrical, is transferred between a source and a load, such as in acoustics or optics.
Theory
Impedance is the opposition by a system to the flow of energy from a source. For constant signals, this impedance can also be constant. For varying signals, it usually changes with frequency. The energy involved can be electrical, mechanical, acoustic, magnetic, electromagnetic, or thermal. The concept of electrical impedance is perhaps the most commonly known. Electrical impedance, like electrical resistance, is measured in ohms. In general, impedance (symbol: Z) has a complex value; this means that loads generally have a resistance component (symbol: R) which forms the real part and a reactance component (symbol: X) which forms the imaginary part.
In simple cases (such as low-frequency or direct current power transmission) the reactance may be negligible or zero; the impedance can be considered a pure resistance, expressed as a real number. In the following summary we will consider the general case when resistance and reactance are both significant, and the special case in which the reactance is negligible.
Maximum power transfer matching
Complex conjugate matching is used when maximum power transfer is required, namely
where a superscript * indicates the complex conjugate. A conjugate match is different from a reflection-less match when either the source or load has a reactive component.
If the source has a reactive component, but the load is purely resistive, then matching can be achieved by adding a reactance of the same magnitude but opposite sign to the load. This simple matching network, consisting of a single element, will usually achieve a perfect match at only a single frequency. This is because the added element will either be a capacitor or an inductor, whose impedance in both cases is frequency dependent, and will not, in general, follow the frequency dependence of the source impedance. For wide bandwidth applications, a more complex network must be designed.
Power transfer
Main article: Maximum power theoremWhenever a source of power with a fixed output impedance such as an electric signal source, a radio transmitter or a mechanical sound (e.g., a loudspeaker) operates into a load, the maximum possible power is delivered to the load when the impedance of the load (load impedance or input impedance) is equal to the complex conjugate of the impedance of the source (that is, its internal impedance or output impedance). For two impedances to be complex conjugates their resistances must be equal, and their reactances must be equal in magnitude but of opposite signs. In low-frequency or DC systems (or systems with purely resistive sources and loads) the reactances are zero, or small enough to be ignored. In this case, maximum power transfer occurs when the resistance of the load is equal to the resistance of the source (see maximum power theorem for a mathematical proof).
Impedance matching is not always necessary. For example, if delivering a high voltage (to reduce signal degradation or to reduce power consumption) is more important than maximizing power transfer, then impedance bridging or voltage bridging is often used.
In older audio systems (reliant on transformers and passive filter networks, and based on the telephone system), the source and load resistances were matched at 600 ohms. One reason for this was to maximize power transfer, as there were no amplifiers available that could restore lost signal. Another reason was to ensure correct operation of the hybrid transformers used at central exchange equipment to separate outgoing from incoming speech, so these could be amplified or fed to a four-wire circuit. Most modern audio circuits, on the other hand, use active amplification and filtering and can use voltage-bridging connections for greatest accuracy. Strictly speaking, impedance matching only applies when both source and load devices are linear; however, matching may be obtained between nonlinear devices within certain operating ranges.
Impedance-matching devices
Adjusting the source impedance or the load impedance, in general, is called "impedance matching". There are three ways to improve an impedance mismatch, all of which are called "impedance matching":
- Devices intended to present an apparent load to the source of Zload = Zsource* (complex conjugate matching). Given a source with a fixed voltage and fixed source impedance, the maximum power theorem says this is the only way to extract the maximum power from the source.
- Devices intended to present an apparent load of Zload = Zline (complex impedance matching), to avoid echoes. Given a transmission line source with a fixed source impedance, this "reflectionless impedance matching" at the end of the transmission line is the only way to avoid reflecting echoes back to the transmission line.
- Devices intended to present an apparent source resistance as close to zero as possible, or presenting an apparent source voltage as high as possible. This is the only way to maximize energy efficiency, and so it is used at the beginning of electrical power lines. Such an impedance bridging connection also minimizes distortion and electromagnetic interference; it is also used in modern audio amplifiers and signal-processing devices.
There are a variety of devices used between a source of energy and a load that perform "impedance matching". To match electrical impedances, engineers use combinations of transformers, resistors, inductors, capacitors and transmission lines. These passive (and active) impedance-matching devices are optimized for different applications and include baluns, antenna tuners (sometimes called ATUs or roller-coasters, because of their appearance), acoustic horns, matching networks, and terminators.
Transformers
Transformers are sometimes used to match the impedances of circuits. A transformer converts alternating current at one voltage to the same waveform at another voltage. The power input to the transformer and output from the transformer is the same (except for conversion losses). The side with the lower voltage is at low impedance (because this has the lower number of turns), and the side with the higher voltage is at a higher impedance (as it has more turns in its coil).
One example of this method involves a television balun transformer. This transformer allows interfacing a balanced line (300-ohm twin-lead) and an unbalanced line (75-ohm coaxial cable such as RG-6). To match the impedances, both cables must be connected to a matching transformer with a turns ratio of 2:1. In this example, the 300-ohm line is connected to the transformer side with more turns; the 75-ohm cable is connected to the transformer side with fewer turns. The formula for calculating the transformer turns ratio for this example is:
Resistive network
Resistive impedance matches are easiest to design and can be achieved with a simple L pad consisting of two resistors. Power loss is an unavoidable consequence of using resistive networks, and they are only (usually) used to transfer line level signals.
Stepped transmission line
Most lumped-element devices can match a specific range of load impedances. For example, in order to match an inductive load into a real impedance, a capacitor needs to be used. If the load impedance becomes capacitive, the matching element must be replaced by an inductor. In many cases, there is a need to use the same circuit to match a broad range of load impedance and thus simplify the circuit design. This issue was addressed by the stepped transmission line, where multiple, serially placed, quarter-wave dielectric slugs are used to vary a transmission line's characteristic impedance. By controlling the position of each element, a broad range of load impedances can be matched without having to reconnect the circuit.
Filters
Filters are frequently used to achieve impedance matching in telecommunications and radio engineering. In general, it is not theoretically possible to achieve perfect impedance matching at all frequencies with a network of discrete components. Impedance matching networks are designed with a definite bandwidth, take the form of a filter, and use filter theory in their design.
Applications requiring only a narrow bandwidth, such as radio tuners and transmitters, might use a simple tuned filter such as a stub. This would provide a perfect match at one specific frequency only. Wide bandwidth matching requires filters with multiple sections.
L-section
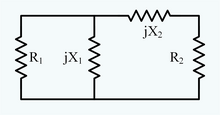
A simple electrical impedance-matching network requires one capacitor and one inductor. In the figure to the right, R1 > R2, however, either R1 or R2 may be the source and the other the load. One of X1 or X2 must be an inductor and the other must be a capacitor. One reactance is in parallel with the source (or load), and the other is in series with the load (or source). If a reactance is in parallel with the source, the effective network matches from high to low impedance.
The analysis is as follows. Consider a real source impedance of and real load impedance of . If a reactance is in parallel with the source impedance, the combined impedance can be written as:
If the imaginary part of the above impedance is canceled by the series reactance, the real part is
Solving for
- .
- .
- where .
Note, , the reactance in parallel, has a negative reactance because it is typically a capacitor. This gives the L-network the additional feature of harmonic suppression since it is a low pass filter too.
The inverse connection (impedance step-up) is simply the reverse—for example, reactance in series with the source. The magnitude of the impedance ratio is limited by reactance losses such as the Q of the inductor. Multiple L-sections can be wired in cascade to achieve higher impedance ratios or greater bandwidth. Transmission line matching networks can be modeled as infinitely many L-sections wired in cascade. Optimal matching circuits can be designed for a particular system using Smith charts.
Power factor correction
Power factor correction devices are intended to cancel the reactive and nonlinear characteristics of a load at the end of a power line. This causes the load seen by the power line to be purely resistive. For a given true power required by a load this minimizes the true current supplied through the power lines, and minimizes power wasted in the resistance of those power lines. For example, a maximum power point tracker is used to extract the maximum power from a solar panel and efficiently transfer it to batteries, the power grid or other loads. The maximum power theorem applies to its "upstream" connection to the solar panel, so it emulates a load resistance equal to the solar panel source resistance. However, the maximum power theorem does not apply to its "downstream" connection. That connection is an impedance bridging connection; it emulates a high-voltage, low-resistance source to maximize efficiency.
On the power grid the overall load is usually inductive. Consequently, power factor correction is most commonly achieved with banks of capacitors. It is only necessary for correction to be achieved at one single frequency, the frequency of the supply. Complex networks are only required when a band of frequencies must be matched and this is the reason why simple capacitors are all that is usually required for power factor correction.
Transmission lines
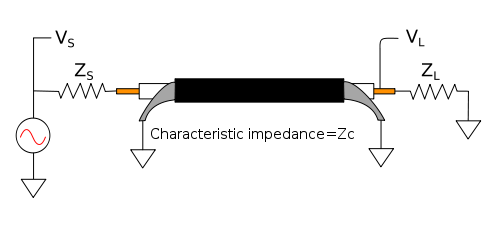
In RF connections, impedance matching is desirable, because otherwise reflections may be created at the end of the mismatched transmission line. The reflection may cause frequency-dependent loss.
In electrical systems involving transmission lines (such as radio and fiber optics)—where the length of the line is long compared to the wavelength of the signal (the signal changes rapidly compared to the time it takes to travel from source to load)— the impedances at each end of the line may be matched to the transmission line's characteristic impedance () to prevent reflections of the signal at the ends of the line. In radio-frequency (RF) systems, a common value for source and load impedances is 50 ohms. A typical RF load is a quarter-wave ground plane antenna (37 ohms with an ideal ground plane).
The general form of the voltage reflection coefficient for a wave moving from medium 1 to medium 2 is given by
while the voltage reflection coefficient for a wave moving from medium 2 to medium 1 is
so the reflection coefficient is the same (except for sign), no matter from which direction the wave approaches the boundary.
There is also a current reflection coefficient, which is the negative of the voltage reflection coefficient. If the wave encounters an open at the load end, positive voltage and negative current pulses are transmitted back toward the source (negative current means the current is going the opposite direction). Thus, at each boundary there are four reflection coefficients (voltage and current on one side, and voltage and current on the other side). All four are the same, except that two are positive and two are negative. The voltage reflection coefficient and current reflection coefficient on the same side have opposite signs. Voltage reflection coefficients on opposite sides of the boundary have opposite signs.
Because they are all the same except for sign it is traditional to interpret the reflection coefficient as the voltage reflection coefficient (unless otherwise indicated). Either end (or both ends) of a transmission line can be a source or a load (or both), so there is no inherent preference for which side of the boundary is medium 1 and which side is medium 2. With a single transmission line it is customary to define the voltage reflection coefficient for a wave incident on the boundary from the transmission line side, regardless of whether a source or load is connected on the other side.
Single-source transmission line driving a load
Load-end conditions
In a transmission line, a wave travels from the source along the line. Suppose the wave hits a boundary (an abrupt change in impedance). Some of the wave is reflected back, while some keeps moving onwards. (Assume there is only one boundary, at the load.)
Let
- and be the voltage and current that is incident on the boundary from the source side.
- and be the voltage and current that is transmitted to the load.
- and be the voltage and current that is reflected back toward the source.
On the line side of the boundary and and on the load side where , , , , , and are phasors.
At a boundary, voltage and current must be continuous, therefore
All these conditions are satisfied by
where is the reflection coefficient going from the transmission line to the load.
Source-end conditions
At the source end of the transmission line, there may be waves incident both from the source and from the line; a reflection coefficient for each direction may be computed with
- ,
where Zs is the source impedance. The source of waves incident from the line are the reflections from the load end. If the source impedance matches the line, reflections from the load end will be absorbed at the source end. If the transmission line is not matched at both ends reflections from the load will be re-reflected at the source and re-re-reflected at the load end ad infinitum, losing energy on each transit of the transmission line. This can cause a resonance condition and strongly frequency-dependent behavior. In a narrow-band system this can be desirable for matching, but is generally undesirable in a wide-band system.
Source-end impedance
where is the one-way transfer function (from either end to the other) when the transmission line is exactly matched at source and load. accounts for everything that happens to the signal in transit (including delay, attenuation and dispersion). If there is a perfect match at the load, and
Transfer function
where is the open circuit (or unloaded) output voltage from the source.
Note that if there is a perfect match at both ends
- and
and then
- .
Electrical examples
Telephone systems
Telephone systems also use matched impedances to minimise echo on long-distance lines. This is related to transmission-line theory. Matching also enables the telephone hybrid coil (2- to 4-wire conversion) to operate correctly. As the signals are sent and received on the same two-wire circuit to the central office (or exchange), cancellation is necessary at the telephone earpiece so excessive sidetone is not heard. All devices used in telephone signal paths are generally dependent on matched cable, source and load impedances. In the local loop, the impedance chosen is 600 ohms (nominal). Terminating networks are installed at the exchange to offer the best match to their subscriber lines. Each country has its own standard for these networks, but they are all designed to approximate about 600 ohms over the voice frequency band.
Loudspeaker amplifiers
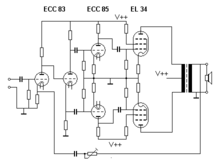
Audio amplifiers typically do not match impedances, but provide an output impedance that is lower than the load impedance (such as < 0.1 ohm in typical semiconductor amplifiers), for improved speaker damping. For vacuum tube amplifiers, impedance-changing transformers are often used to get a low output impedance, and to better match the amplifier's performance to the load impedance. Some tube amplifiers have output transformer taps to adapt the amplifier output to typical loudspeaker impedances.
The output transformer in vacuum-tube-based amplifiers has two basic functions:
- Separation of the AC component (which contains the audio signals) from the DC component (supplied by the power supply) in the anode circuit of a vacuum-tube-based power stage. A loudspeaker should not be subjected to DC current.
- Reducing the output impedance of power pentodes (such as the EL34) in a common-cathode configuration.
The impedance of the loudspeaker on the secondary coil of the transformer will be transformed to a higher impedance on the primary coil in the circuit of the power pentodes by the square of the turns ratio, which forms the impedance scaling factor.
The output stage in common-drain or common-collector semiconductor-based end stages with MOSFETs or power transistors has a very low output impedance. If they are properly balanced, there is no need for a transformer or a large electrolytic capacitor to separate AC from DC current.
Non-electrical examples
Acoustics
Similar to electrical transmission lines, an impedance matching problem exists when transferring sound energy from one medium to another. If the acoustic impedance of the two media are very different most sound energy will be reflected (or absorbed), rather than transferred across the border. The gel used in medical ultrasonography helps transfer acoustic energy from the transducer to the body and back again. Without the gel, the impedance mismatch in the transducer-to-air and the air-to-body discontinuity reflects almost all the energy, leaving very little to go into the body.
The bones in the middle ear function as a series of levers, which matches mechanical impedance between the eardrum (which is acted upon by vibrations in air) and the fluid-filled inner ear.
Horns in loudspeaker systems are used like transformers in electrical circuits to match the impedance of the transducer to the impedance of the air. This principle is used in both horn loudspeakers and musical instruments. Because most driver impedances are poorly matched to the impedance of free air at low frequencies, loudspeaker enclosures are designed to both match impedance and minimize destructive phase cancellations between output from the front and rear of a speaker cone. The loudness of sound produced in air from a loudspeaker is directly related to the ratio of the diameter of the speaker to the wavelength of the sound being produced: larger speakers can produce lower frequencies at a higher level than smaller speakers. Elliptical speakers are a complex case, acting like large speakers lengthwise and small speakers crosswise. Acoustic impedance matching (or the lack of it) affects the operation of a megaphone, an echo and soundproofing.
Optics
A similar effect occurs when light (or any electromagnetic wave) hits the interface between two media with different refractive indices. For non-magnetic materials, the refractive index is inversely proportional to the material's characteristic impedance. An optical or wave impedance (that depends on the propagation direction) can be calculated for each medium, and may be used in the transmission-line reflection equation
to calculate reflection and transmission coefficients for the interface. For non-magnetic dielectrics, this equation is equivalent to the Fresnel equations. Unwanted reflections can be reduced by the use of an anti-reflection optical coating.
Mechanics
If a body of mass m collides elastically with a second body, maximum energy transfer to the second body will occur when the second body has the same mass m. In a head-on collision of equal masses, the energy of the first body will be completely transferred to the second body (as in Newton's cradle for example). In this case, the masses act as "mechanical impedances", which must be matched to maximize energy transfer.
If and are the masses of the moving and stationary bodies, and P is the momentum of the system (which remains constant throughout the collision), the energy of the second body after the collision will be E2:
which is analogous to the power-transfer equation.

If we cannot change the masses of bodies, then we can match their impedance with a lever. Imagine a large ball dropping to the ground, and a small ball lying on the ground. The large ball hits the short end of a lever, and the small ball is launched from the long end of the lever. If the lever arm lengths satisfy , then all energy would be transferred to the small ball if collisions are elastic. This is roughly how the middle ear works (see above).
These principles are useful in the application of highly energetic materials (explosives). If an explosive charge is placed on a target, the sudden release of energy causes compression waves to propagate through the target radially from the point-charge contact. When the compression waves reach areas of high acoustic impedance mismatch (such as the opposite side of the target), tension waves reflect back and create spalling. The greater the mismatch, the greater the effect of creasing and spalling will be. A charge initiated against a wall with air behind it will do more damage to the wall than a charge initiated against a wall with soil behind it.
See also
Notes
- Qian, Chunqui; Brey, William W. (July 2009). "Impedance matching with an adjustable segmented transmission line". Journal of Magnetic Resonance. 199 (1): 104–110. Bibcode:2009JMagR.199..104Q. doi:10.1016/j.jmr.2009.04.005. PMID 19406676.
- Pozar, David. Microwave Engineering (3rd ed.). p. 223.
- Hayward, Wes (1994). Introduction to Radio Frequency Design. ARRL. p. 138. ISBN 0-87259-492-0.
- Kraus (1984, p. 407)
- Sadiku (1989, pp. 505–507)
- Hayt (1989, pp. 398–401)
- Karakash (1950, pp. 52–57)
References
- Floyd, Thomas (1997), Principles of Electric Circuits (5th ed.), Prentice Hall, ISBN 0-13-232224-2
- Hayt, William (1989), Engineering Electromagnetics (5th ed.), McGraw-Hill, ISBN 0-07-027406-1
- Karakash, John J. (1950), Transmission Lines and Filter Networks (1st ed.), Macmillan
- Kraus, John D. (1984), Electromagnetics (3rd ed.), McGraw-Hill, ISBN 0-07-035423-5
- Sadiku, Matthew N. O. (1989), Elements of Electromagnetics (1st ed.), Saunders College Publishing, ISBN 0030134846
- Stutzman, Warren L.; Thiele, Gary (2012), Antenna Theory and Design, John Wiley & Sons, ISBN 978-0470576649
- Young, E. C. (1988), "maximum power theorem", The Penguin Dictionary of Electronics, Penguin, ISBN 0-14-051187-3
Further reading
- Thomas, Robert L. A Practical Introduction to Impedance Matching (PDF). Radiating Systems Design / Avionics Engineering, Douglas Aircraft Company. Archived (PDF) from the original on 2023-07-23. Retrieved 2023-07-23. (175 pages)
External links
- Impedance Matching Impedance Matching with the Smith Chart


 and real load impedance of
and real load impedance of  . If a reactance
. If a reactance  is in parallel with the source impedance, the combined impedance can be written as:
is in parallel with the source impedance, the combined impedance can be written as:


 .
. .
. .
. ) to prevent reflections of the signal at the ends of the line. In radio-frequency (RF) systems, a common value for source and load impedances is 50
) to prevent reflections of the signal at the ends of the line. In radio-frequency (RF) systems, a common value for source and load impedances is 50 


 and
and  be the voltage and current that is incident on the boundary from the source side.
be the voltage and current that is incident on the boundary from the source side. and
and  be the voltage and current that is transmitted to the load.
be the voltage and current that is transmitted to the load. and
and  be the voltage and current that is reflected back toward the source.
be the voltage and current that is reflected back toward the source. and
and  and on the load side
and on the load side  where
where 





 is the
is the 
 ,
,
 is the one-way transfer function (from either end to the other) when the transmission line is exactly matched at source and load.
is the one-way transfer function (from either end to the other) when the transmission line is exactly matched at source and load.  accounts for everything that happens to the signal in transit (including delay, attenuation and dispersion). If there is a perfect match at the load,
accounts for everything that happens to the signal in transit (including delay, attenuation and dispersion). If there is a perfect match at the load,  and
and 

 is the open circuit (or unloaded) output voltage from the source.
is the open circuit (or unloaded) output voltage from the source.

 .
.
 and
and  are the masses of the moving and stationary bodies, and P is the momentum of the system (which remains constant throughout the collision), the energy of the second body after the collision will be E2:
are the masses of the moving and stationary bodies, and P is the momentum of the system (which remains constant throughout the collision), the energy of the second body after the collision will be E2:

 , then all energy would be transferred to the small ball if collisions are elastic. This is roughly how the middle ear works (see above).
, then all energy would be transferred to the small ball if collisions are elastic. This is roughly how the middle ear works (see above).