Neural coding

(Redirected from Independent-spike coding) Method by which information is represented in the brain

Neural coding (or neural representation) is a neuroscience field concerned with characterising the hypothetical relationship between the stimulus and the neuronal responses, and the relationship among the electrical activities of the neurons in the ensemble. Based on the theory that sensory and other information is represented in the brain by networks of neurons, it is believed that neurons can encode both digital and analog information.

Overview

Neurons have an ability uncommon among the cells of the body to propagate signals rapidly over large distances by generating characteristic electrical pulses called action potentials: voltage spikes that can travel down axons. Sensory neurons change their activities by firing sequences of action potentials in various temporal patterns, with the presence of external sensory stimuli, such as light, sound, taste, smell and touch. Information about the stimulus is encoded in this pattern of action potentials and transmitted into and around the brain. Beyond this, specialized neurons, such as those of the retina, can communicate more information through graded potentials. These differ from action potentials because information about the strength of a stimulus directly correlates with the strength of the neurons' output. The signal decays much faster for graded potentials, necessitating short inter-neuron distances and high neuronal density. The advantage of graded potentials is higher information rates capable of encoding more states (i.e. higher fidelity) than spiking neurons.

Although action potentials can vary somewhat in duration, amplitude and shape, they are typically treated as identical stereotyped events in neural coding studies. If the brief duration of an action potential (about 1 ms) is ignored, an action potential sequence, or spike train, can be characterized simply by a series of all-or-none point events in time. The lengths of interspike intervals (ISIs) between two successive spikes in a spike train often vary, apparently randomly. The study of neural coding involves measuring and characterizing how stimulus attributes, such as light or sound intensity, or motor actions, such as the direction of an arm movement, are represented by neuron action potentials or spikes. In order to describe and analyze neuronal firing, statistical methods and methods of probability theory and stochastic point processes have been widely applied.

With the development of large-scale neural recording and decoding technologies, researchers have begun to crack the neural code and have already provided the first glimpse into the real-time neural code as memory is formed and recalled in the hippocampus, a brain region known to be central for memory formation. Neuroscientists have initiated several large-scale brain decoding projects.

Encoding and decoding

The link between stimulus and response can be studied from two opposite points of view. Neural encoding refers to the map from stimulus to response. The main focus is to understand how neurons respond to a wide variety of stimuli, and to construct models that attempt to predict responses to other stimuli. Neural decoding refers to the reverse map, from response to stimulus, and the challenge is to reconstruct a stimulus, or certain aspects of that stimulus, from the spike sequences it evokes.

Hypothesized coding schemes

A sequence, or 'train', of spikes may contain information based on different coding schemes. In some neurons the strength with which a postsynaptic partner responds may depend solely on the 'firing rate', the average number of spikes per unit time (a 'rate code'). At the other end, a complex 'temporal code' is based on the precise timing of single spikes. They may be locked to an external stimulus such as in the visual and auditory system or be generated intrinsically by the neural circuitry.

Whether neurons use rate coding or temporal coding is a topic of intense debate within the neuroscience community, even though there is no clear definition of what these terms mean.

Rate code

The rate coding model of neuronal firing communication states that as the intensity of a stimulus increases, the frequency or rate of action potentials, or "spike firing", increases. Rate coding is sometimes called frequency coding.

Rate coding is a traditional coding scheme, assuming that most, if not all, information about the stimulus is contained in the firing rate of the neuron. Because the sequence of action potentials generated by a given stimulus varies from trial to trial, neuronal responses are typically treated statistically or probabilistically. They may be characterized by firing rates, rather than as specific spike sequences. In most sensory systems, the firing rate increases, generally non-linearly, with increasing stimulus intensity. Under a rate coding assumption, any information possibly encoded in the temporal structure of the spike train is ignored. Consequently, rate coding is inefficient but highly robust with respect to the ISI 'noise'.

During rate coding, precisely calculating firing rate is very important. In fact, the term "firing rate" has a few different definitions, which refer to different averaging procedures, such as an average over time (rate as a single-neuron spike count) or an average over several repetitions (rate of PSTH) of experiment.

In rate coding, learning is based on activity-dependent synaptic weight modifications.

Rate coding was originally shown by Edgar Adrian and Yngve Zotterman in 1926. In this simple experiment different weights were hung from a muscle. As the weight of the stimulus increased, the number of spikes recorded from sensory nerves innervating the muscle also increased. From these original experiments, Adrian and Zotterman concluded that action potentials were unitary events, and that the frequency of events, and not individual event magnitude, was the basis for most inter-neuronal communication.

In the following decades, measurement of firing rates became a standard tool for describing the properties of all types of sensory or cortical neurons, partly due to the relative ease of measuring rates experimentally. However, this approach neglects all the information possibly contained in the exact timing of the spikes. During recent years, more and more experimental evidence has suggested that a straightforward firing rate concept based on temporal averaging may be too simplistic to describe brain activity.

Spike-count rate (average over time)

The spike-count rate, also referred to as temporal average, is obtained by counting the number of spikes that appear during a trial and dividing by the duration of trial. The length T of the time window is set by the experimenter and depends on the type of neuron recorded from and to the stimulus. In practice, to get sensible averages, several spikes should occur within the time window. Typical values are T = 100 ms or T = 500 ms, but the duration may also be longer or shorter (Chapter 1.5 in the textbook 'Spiking Neuron Models' ).

The spike-count rate can be determined from a single trial, but at the expense of losing all temporal resolution about variations in neural response during the course of the trial. Temporal averaging can work well in cases where the stimulus is constant or slowly varying and does not require a fast reaction of the organism — and this is the situation usually encountered in experimental protocols. Real-world input, however, is hardly stationary, but often changing on a fast time scale. For example, even when viewing a static image, humans perform saccades, rapid changes of the direction of gaze. The image projected onto the retinal photoreceptors changes therefore every few hundred milliseconds (Chapter 1.5 in )

Despite its shortcomings, the concept of a spike-count rate code is widely used not only in experiments, but also in models of neural networks. It has led to the idea that a neuron transforms information about a single input variable (the stimulus strength) into a single continuous output variable (the firing rate).

There is a growing body of evidence that in Purkinje neurons, at least, information is not simply encoded in firing but also in the timing and duration of non-firing, quiescent periods. There is also evidence from retinal cells, that information is encoded not only in the firing rate but also in spike timing. More generally, whenever a rapid response of an organism is required a firing rate defined as a spike-count over a few hundred milliseconds is simply too slow.

Time-dependent firing rate (averaging over several trials)

The time-dependent firing rate is defined as the average number of spikes (averaged over trials) appearing during a short interval between times t and t+Δt, divided by the duration of the interval. It works for stationary as well as for time-dependent stimuli. To experimentally measure the time-dependent firing rate, the experimenter records from a neuron while stimulating with some input sequence. The same stimulation sequence is repeated several times and the neuronal response is reported in a Peri-Stimulus-Time Histogram (PSTH). The time t is measured with respect to the start of the stimulation sequence. The Δt must be large enough (typically in the range of one or a few milliseconds) so that there is a sufficient number of spikes within the interval to obtain a reliable estimate of the average. The number of occurrences of spikes n_K(t;t+Δt) summed over all repetitions of the experiment divided by the number K of repetitions is a measure of the typical activity of the neuron between time t and t+Δt. A further division by the interval length Δt yields time-dependent firing rate r(t) of the neuron, which is equivalent to the spike density of PSTH (Chapter 1.5 in ).

For sufficiently small Δt, r(t)Δt is the average number of spikes occurring between times t and t+Δt over multiple trials. If Δt is small, there will never be more than one spike within the interval between t and t+Δt on any given trial. This means that r(t)Δt is also the fraction of trials on which a spike occurred between those times. Equivalently, r(t)Δt is the probability that a spike occurs during this time interval.

As an experimental procedure, the time-dependent firing rate measure is a useful method to evaluate neuronal activity, in particular in the case of time-dependent stimuli. The obvious problem with this approach is that it can not be the coding scheme used by neurons in the brain. Neurons can not wait for the stimuli to repeatedly present in an exactly same manner before generating a response.

Nevertheless, the experimental time-dependent firing rate measure can make sense, if there are large populations of independent neurons that receive the same stimulus. Instead of recording from a population of N neurons in a single run, it is experimentally easier to record from a single neuron and average over N repeated runs. Thus, the time-dependent firing rate coding relies on the implicit assumption that there are always populations of neurons.

Temporal coding

When precise spike timing or high-frequency firing-rate fluctuations are found to carry information, the neural code is often identified as a temporal code. A number of studies have found that the temporal resolution of the neural code is on a millisecond time scale, indicating that precise spike timing is a significant element in neural coding. Such codes, that communicate via the time between spikes are also referred to as interpulse interval codes, and have been supported by recent studies.

Neurons exhibit high-frequency fluctuations of firing-rates which could be noise or could carry information. Rate coding models suggest that these irregularities are noise, while temporal coding models suggest that they encode information. If the nervous system only used rate codes to convey information, a more consistent, regular firing rate would have been evolutionarily advantageous, and neurons would have utilized this code over other less robust options. Temporal coding supplies an alternate explanation for the “noise," suggesting that it actually encodes information and affects neural processing. To model this idea, binary symbols can be used to mark the spikes: 1 for a spike, 0 for no spike. Temporal coding allows the sequence 000111000111 to mean something different from 001100110011, even though the mean firing rate is the same for both sequences, at 6 spikes/10 ms.

Until recently, scientists had put the most emphasis on rate encoding as an explanation for post-synaptic potential patterns. However, functions of the brain are more temporally precise than the use of only rate encoding seems to allow. In other words, essential information could be lost due to the inability of the rate code to capture all the available information of the spike train. In addition, responses are different enough between similar (but not identical) stimuli to suggest that the distinct patterns of spikes contain a higher volume of information than is possible to include in a rate code.

Temporal codes (also called spike codes ), employ those features of the spiking activity that cannot be described by the firing rate. For example, time-to-first-spike after the stimulus onset, phase-of-firing with respect to background oscillations, characteristics based on the second and higher statistical moments of the ISI probability distribution, spike randomness, or precisely timed groups of spikes (temporal patterns) are candidates for temporal codes. As there is no absolute time reference in the nervous system, the information is carried either in terms of the relative timing of spikes in a population of neurons (temporal patterns) or with respect to an ongoing brain oscillation (phase of firing). One way in which temporal codes are decoded, in presence of neural oscillations, is that spikes occurring at specific phases of an oscillatory cycle are more effective in depolarizing the post-synaptic neuron.

The temporal structure of a spike train or firing rate evoked by a stimulus is determined both by the dynamics of the stimulus and by the nature of the neural encoding process. Stimuli that change rapidly tend to generate precisely timed spikes (and rapidly changing firing rates in PSTHs) no matter what neural coding strategy is being used. Temporal coding in the narrow sense refers to temporal precision in the response that does not arise solely from the dynamics of the stimulus, but that nevertheless relates to properties of the stimulus. The interplay between stimulus and encoding dynamics makes the identification of a temporal code difficult.

In temporal coding, learning can be explained by activity-dependent synaptic delay modifications. The modifications can themselves depend not only on spike rates (rate coding) but also on spike timing patterns (temporal coding), i.e., can be a special case of spike-timing-dependent plasticity.

The issue of temporal coding is distinct and independent from the issue of independent-spike coding. If each spike is independent of all the other spikes in the train, the temporal character of the neural code is determined by the behavior of time-dependent firing rate r(t). If r(t) varies slowly with time, the code is typically called a rate code, and if it varies rapidly, the code is called temporal.

Temporal coding in sensory systems

For very brief stimuli, a neuron's maximum firing rate may not be fast enough to produce more than a single spike. Due to the density of information about the abbreviated stimulus contained in this single spike, it would seem that the timing of the spike itself would have to convey more information than simply the average frequency of action potentials over a given period of time. This model is especially important for sound localization, which occurs within the brain on the order of milliseconds. The brain must obtain a large quantity of information based on a relatively short neural response. Additionally, if low firing rates on the order of ten spikes per second must be distinguished from arbitrarily close rate coding for different stimuli, then a neuron trying to discriminate these two stimuli may need to wait for a second or more to accumulate enough information. This is not consistent with numerous organisms which are able to discriminate between stimuli in the time frame of milliseconds, suggesting that a rate code is not the only model at work.

To account for the fast encoding of visual stimuli, it has been suggested that neurons of the retina encode visual information in the latency time between stimulus onset and first action potential, also called latency to first spike or time-to-first-spike. This type of temporal coding has been shown also in the auditory and somato-sensory system. The main drawback of such a coding scheme is its sensitivity to intrinsic neuronal fluctuations. In the primary visual cortex of macaques, the timing of the first spike relative to the start of the stimulus was found to provide more information than the interval between spikes. However, the interspike interval could be used to encode additional information, which is especially important when the spike rate reaches its limit, as in high-contrast situations. For this reason, temporal coding may play a part in coding defined edges rather than gradual transitions.

The mammalian gustatory system is useful for studying temporal coding because of its fairly distinct stimuli and the easily discernible responses of the organism. Temporally encoded information may help an organism discriminate between different tastants of the same category (sweet, bitter, sour, salty, umami) that elicit very similar responses in terms of spike count. The temporal component of the pattern elicited by each tastant may be used to determine its identity (e.g., the difference between two bitter tastants, such as quinine and denatonium). In this way, both rate coding and temporal coding may be used in the gustatory system – rate for basic tastant type, temporal for more specific differentiation.

Research on mammalian gustatory system has shown that there is an abundance of information present in temporal patterns across populations of neurons, and this information is different from that which is determined by rate coding schemes. Groups of neurons may synchronize in response to a stimulus. In studies dealing with the front cortical portion of the brain in primates, precise patterns with short time scales only a few milliseconds in length were found across small populations of neurons which correlated with certain information processing behaviors. However, little information could be determined from the patterns; one possible theory is they represented the higher-order processing taking place in the brain.

As with the visual system, in mitral/tufted cells in the olfactory bulb of mice, first-spike latency relative to the start of a sniffing action seemed to encode much of the information about an odor. This strategy of using spike latency allows for rapid identification of and reaction to an odorant. In addition, some mitral/tufted cells have specific firing patterns for given odorants. This type of extra information could help in recognizing a certain odor, but is not completely necessary, as average spike count over the course of the animal's sniffing was also a good identifier. Along the same lines, experiments done with the olfactory system of rabbits showed distinct patterns which correlated with different subsets of odorants, and a similar result was obtained in experiments with the locust olfactory system.

Temporal coding applications

The specificity of temporal coding requires highly refined technology to measure informative, reliable, experimental data. Advances made in optogenetics allow neurologists to control spikes in individual neurons, offering electrical and spatial single-cell resolution. For example, blue light causes the light-gated ion channel channelrhodopsin to open, depolarizing the cell and producing a spike. When blue light is not sensed by the cell, the channel closes, and the neuron ceases to spike. The pattern of the spikes matches the pattern of the blue light stimuli. By inserting channelrhodopsin gene sequences into mouse DNA, researchers can control spikes and therefore certain behaviors of the mouse (e.g., making the mouse turn left). Researchers, through optogenetics, have the tools to effect different temporal codes in a neuron while maintaining the same mean firing rate, and thereby can test whether or not temporal coding occurs in specific neural circuits.

Optogenetic technology also has the potential to enable the correction of spike abnormalities at the root of several neurological and psychological disorders. If neurons do encode information in individual spike timing patterns, key signals could be missed by attempting to crack the code while looking only at mean firing rates. Understanding any temporally encoded aspects of the neural code and replicating these sequences in neurons could allow for greater control and treatment of neurological disorders such as depression, schizophrenia, and Parkinson's disease. Regulation of spike intervals in single cells more precisely controls brain activity than the addition of pharmacological agents intravenously.

Phase-of-firing code

Main article: Phase precession Further information: Phase resetting in neurons

Phase-of-firing code is a neural coding scheme that combines the spike count code with a time reference based on oscillations. This type of code takes into account a time label for each spike according to a time reference based on phase of local ongoing oscillations at low or high frequencies.

It has been shown that neurons in some cortical sensory areas encode rich naturalistic stimuli in terms of their spike times relative to the phase of ongoing network oscillatory fluctuations, rather than only in terms of their spike count. The local field potential signals reflect population (network) oscillations. The phase-of-firing code is often categorized as a temporal code although the time label used for spikes (i.e. the network oscillation phase) is a low-resolution (coarse-grained) reference for time. As a result, often only four discrete values for the phase are enough to represent all the information content in this kind of code with respect to the phase of oscillations in low frequencies. Phase-of-firing code is loosely based on the phase precession phenomena observed in place cells of the hippocampus. Another feature of this code is that neurons adhere to a preferred order of spiking between a group of sensory neurons, resulting in firing sequence.

Phase code has been shown in visual cortex to involve also high-frequency oscillations. Within a cycle of gamma oscillation, each neuron has its own preferred relative firing time. As a result, an entire population of neurons generates a firing sequence that has a duration of up to about 15 ms.

Population coding

Population coding is a method to represent stimuli by using the joint activities of a number of neurons. In population coding, each neuron has a distribution of responses over some set of inputs, and the responses of many neurons may be combined to determine some value about the inputs. From the theoretical point of view, population coding is one of a few mathematically well-formulated problems in neuroscience. It grasps the essential features of neural coding and yet is simple enough for theoretic analysis. Experimental studies have revealed that this coding paradigm is widely used in the sensory and motor areas of the brain.

For example, in the visual area medial temporal (MT), neurons are tuned to the direction of object motion. In response to an object moving in a particular direction, many neurons in MT fire with a noise-corrupted and bell-shaped activity pattern across the population. The moving direction of the object is retrieved from the population activity, to be immune from the fluctuation existing in a single neuron's signal. When monkeys are trained to move a joystick towards a lit target, a single neuron will fire for multiple target directions. However it fires the fastest for one direction and more slowly depending on how close the target was to the neuron's "preferred" direction. If each neuron represents movement in its preferred direction, and the vector sum of all neurons is calculated (each neuron has a firing rate and a preferred direction), the sum points in the direction of motion. In this manner, the population of neurons codes the signal for the motion. This particular population code is referred to as population vector coding.

Place-time population codes, termed the averaged-localized-synchronized-response (ALSR) code, have been derived for neural representation of auditory acoustic stimuli. This exploits both the place or tuning within the auditory nerve, as well as the phase-locking within each nerve fiber auditory nerve. The first ALSR representation was for steady-state vowels; ALSR representations of pitch and formant frequencies in complex, non-steady state stimuli were later demonstrated for voiced-pitch, and formant representations in consonant-vowel syllables. The advantage of such representations is that global features such as pitch or formant transition profiles can be represented as global features across the entire nerve simultaneously via both rate and place coding.

Population coding has a number of other advantages as well, including reduction of uncertainty due to neuronal variability and the ability to represent a number of different stimulus attributes simultaneously. Population coding is also much faster than rate coding and can reflect changes in the stimulus conditions nearly instantaneously. Individual neurons in such a population typically have different but overlapping selectivities, so that many neurons, but not necessarily all, respond to a given stimulus.

Typically an encoding function has a peak value such that activity of the neuron is greatest if the perceptual value is close to the peak value, and becomes reduced accordingly for values less close to the peak value. It follows that the actual perceived value can be reconstructed from the overall pattern of activity in the set of neurons. Vector coding is an example of simple averaging. A more sophisticated mathematical technique for performing such a reconstruction is the method of maximum likelihood based on a multivariate distribution of the neuronal responses. These models can assume independence, second order correlations, or even more detailed dependencies such as higher order maximum entropy models, or copulas.

Correlation coding

The correlation coding model of neuronal firing claims that correlations between action potentials, or "spikes", within a spike train may carry additional information above and beyond the simple timing of the spikes. Early work suggested that correlation between spike trains can only reduce, and never increase, the total mutual information present in the two spike trains about a stimulus feature. However, this was later demonstrated to be incorrect. Correlation structure can increase information content if noise and signal correlations are of opposite sign. Correlations can also carry information not present in the average firing rate of two pairs of neurons. A good example of this exists in the pentobarbital-anesthetized marmoset auditory cortex, in which a pure tone causes an increase in the number of correlated spikes, but not an increase in the mean firing rate, of pairs of neurons.

Independent-spike coding

The independent-spike coding model of neuronal firing claims that each individual action potential, or "spike", is independent of each other spike within the spike train.

Position coding

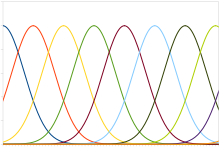
A typical population code involves neurons with a Gaussian tuning curve whose means vary linearly with the stimulus intensity, meaning that the neuron responds most strongly (in terms of spikes per second) to a stimulus near the mean. The actual intensity could be recovered as the stimulus level corresponding to the mean of the neuron with the greatest response. However, the noise inherent in neural responses means that a maximum likelihood estimation function is more accurate.

Neural responses are noisy and unreliable.

This type of code is used to encode continuous variables such as joint position, eye position, color, or sound frequency. Any individual neuron is too noisy to faithfully encode the variable using rate coding, but an entire population ensures greater fidelity and precision. For a population of unimodal tuning curves, i.e. with a single peak, the precision typically scales linearly with the number of neurons. Hence, for half the precision, half as many neurons are required. In contrast, when the tuning curves have multiple peaks, as in grid cells that represent space, the precision of the population can scale exponentially with the number of neurons. This greatly reduces the number of neurons required for the same precision.

Sparse coding

The sparse code is when each item is encoded by the strong activation of a relatively small set of neurons. For each item to be encoded, this is a different subset of all available neurons. In contrast to sensor-sparse coding, sensor-dense coding implies that all information from possible sensor locations is known.

As a consequence, sparseness may be focused on temporal sparseness ("a relatively small number of time periods are active") or on the sparseness in an activated population of neurons. In this latter case, this may be defined in one time period as the number of activated neurons relative to the total number of neurons in the population. This seems to be a hallmark of neural computations since compared to traditional computers, information is massively distributed across neurons. Sparse coding of natural images produces wavelet-like oriented filters that resemble the receptive fields of simple cells in the visual cortex. The capacity of sparse codes may be increased by simultaneous use of temporal coding, as found in the locust olfactory system.

Given a potentially large set of input patterns, sparse coding algorithms (e.g. sparse autoencoder) attempt to automatically find a small number of representative patterns which, when combined in the right proportions, reproduce the original input patterns. The sparse coding for the input then consists of those representative patterns. For example, the very large set of English sentences can be encoded by a small number of symbols (i.e. letters, numbers, punctuation, and spaces) combined in a particular order for a particular sentence, and so a sparse coding for English would be those symbols.

Linear generative model

Most models of sparse coding are based on the linear generative model. In this model, the symbols are combined in a linear fashion to approximate the input.

More formally, given a k-dimensional set of real-numbered input vectors ${\vec {\xi }}\in \mathbb {R} ^{k}$ , the goal of sparse coding is to determine n k-dimensional basis vectors ${\vec {b_{1}}},\ldots ,{\vec {b_{n}}}\in \mathbb {R} ^{k}$ , corresponding to neuronal receptive fields, along with a sparse n-dimensional vector of weights or coefficients ${\vec {s}}\in \mathbb {R} ^{n}$ for each input vector, so that a linear combination of the basis vectors with proportions given by the coefficients results in a close approximation to the input vector: ${\vec {\xi }}\approx \sum _{j=1}^{n}s_{j}{\vec {b}}_{j}$ .

The codings generated by algorithms implementing a linear generative model can be classified into codings with soft sparseness and those with hard sparseness. These refer to the distribution of basis vector coefficients for typical inputs. A coding with soft sparseness has a smooth Gaussian-like distribution, but peakier than Gaussian, with many zero values, some small absolute values, fewer larger absolute values, and very few very large absolute values. Thus, many of the basis vectors are active. Hard sparseness, on the other hand, indicates that there are many zero values, no or hardly any small absolute values, fewer larger absolute values, and very few very large absolute values, and thus few of the basis vectors are active. This is appealing from a metabolic perspective: less energy is used when fewer neurons are firing.

Another measure of coding is whether it is critically complete or overcomplete. If the number of basis vectors n is equal to the dimensionality k of the input set, the coding is said to be critically complete. In this case, smooth changes in the input vector result in abrupt changes in the coefficients, and the coding is not able to gracefully handle small scalings, small translations, or noise in the inputs. If, however, the number of basis vectors is larger than the dimensionality of the input set, the coding is overcomplete. Overcomplete codings smoothly interpolate between input vectors and are robust under input noise. The human primary visual cortex is estimated to be overcomplete by a factor of 500, so that, for example, a 14 x 14 patch of input (a 196-dimensional space) is coded by roughly 100,000 neurons.

Other models are based on matching pursuit, a sparse approximation algorithm which finds the "best matching" projections of multidimensional data, and dictionary learning, a representation learning method which aims to find a sparse matrix representation of the input data in the form of a linear combination of basic elements as well as those basic elements themselves.

Biological evidence

Sparse coding may be a general strategy of neural systems to augment memory capacity. To adapt to their environments, animals must learn which stimuli are associated with rewards or punishments and distinguish these reinforced stimuli from similar but irrelevant ones. Such tasks require implementing stimulus-specific associative memories in which only a few neurons out of a population respond to any given stimulus and each neuron responds to only a few stimuli out of all possible stimuli.

Theoretical work on sparse distributed memory has suggested that sparse coding increases the capacity of associative memory by reducing overlap between representations. Experimentally, sparse representations of sensory information have been observed in many systems, including vision, audition, touch, and olfaction. However, despite the accumulating evidence for widespread sparse coding and theoretical arguments for its importance, a demonstration that sparse coding improves the stimulus-specificity of associative memory has been difficult to obtain.

In the Drosophila olfactory system, sparse odor coding by the Kenyon cells of the mushroom body is thought to generate a large number of precisely addressable locations for the storage of odor-specific memories. Sparseness is controlled by a negative feedback circuit between Kenyon cells and GABAergic anterior paired lateral (APL) neurons. Systematic activation and blockade of each leg of this feedback circuit shows that Kenyon cells activate APL neurons and APL neurons inhibit Kenyon cells. Disrupting the Kenyon cell–APL feedback loop decreases the sparseness of Kenyon cell odor responses, increases inter-odor correlations, and prevents flies from learning to discriminate similar, but not dissimilar, odors. These results suggest that feedback inhibition suppresses Kenyon cell activity to maintain sparse, decorrelated odor coding and thus the odor-specificity of memories.

References

Brown EN, Kass RE, Mitra PP (May 2004). "Multiple neural spike train data analysis: state-of-the-art and future challenges". Nat. Neurosci. 7 (5): 456–61. doi:10.1038/nn1228. PMID 15114358. S2CID 562815.
Johnson, K. O. (June 2000). "Neural coding". Neuron. 26 (3): 563–566. doi:10.1016/S0896-6273(00)81193-9. ISSN 0896-6273. PMID 10896153.
^ Thorpe, S.J. (1990). "Spike arrival times: A highly efficient coding scheme for neural networks". In Eckmiller, R.; Hartmann, G.; Hauske, G. (eds.). Parallel processing in neural systems and computers (PDF). North-Holland. pp. 91–94. ISBN 978-0-444-88390-2.
Sengupta B, Laughlin SB, Niven JE (2014) Consequences of Converting Graded to Action Potentials upon Neural Information Coding and Energy Efficiency. PLOS Computational Biology 10(1): e1003439. https://doi.org/10.1371/journal.pcbi.1003439
Gerstner, Wulfram; Kistler, Werner M. (2002). Spiking Neuron Models: Single Neurons, Populations, Plasticity. Cambridge University Press. ISBN 978-0-521-89079-3.
^ Stein RB, Gossen ER, Jones KE (May 2005). "Neuronal variability: noise or part of the signal?". Nat. Rev. Neurosci. 6 (5): 389–97. doi:10.1038/nrn1668. PMID 15861181. S2CID 205500218.
The Memory Code. http://www.scientificamerican.com/article/the-memory-code/
Chen, G; Wang, LP; Tsien, JZ (2009). "Neural population-level memory traces in the mouse hippocampus". PLOS ONE. 4 (12): e8256. Bibcode:2009PLoSO...4.8256C. doi:10.1371/journal.pone.0008256. PMC 2788416. PMID 20016843.
Zhang, H; Chen, G; Kuang, H; Tsien, JZ (Nov 2013). "Mapping and deciphering neural codes of NMDA receptor-dependent fear memory engrams in the hippocampus". PLOS ONE. 8 (11): e79454. Bibcode:2013PLoSO...879454Z. doi:10.1371/journal.pone.0079454. PMC 3841182. PMID 24302990.
Brain Decoding Project. http://cobweb.cs.uga.edu/~hanbo/brainDecode//?hg=0
The Simons Collaboration on the Global Brain. https://www.simonsfoundation.org/life-sciences/simons-collaboration-global-brain/
Burcas G.T & Albright T.D. Gauging sensory representations in the brain. http://www.vcl.salk.edu/Publications/PDF/Buracas_Albright_1999_TINS.pdf
Gerstner W, Kreiter AK, Markram H, Herz AV (November 1997). "Neural codes: firing rates and beyond". Proc. Natl. Acad. Sci. U.S.A. 94 (24): 12740–1. Bibcode:1997PNAS...9412740G. doi:10.1073/pnas.94.24.12740. PMC 34168. PMID 9398065.
^ Gerstner, Wulfram. (2002). Spiking neuron models : single neurons, populations, plasticity. Kistler, Werner M., 1969-. Cambridge, U.K.: Cambridge University Press. ISBN 0-511-07817-X. OCLC 57417395.
Kandel, E.; Schwartz, J.; Jessel, T.M. (1991). Principles of Neural Science (3rd ed.). Elsevier. ISBN 978-0444015624.
Adrian ED, Zotterman Y (1926). "The impulses produced by sensory nerve endings: Part II: The response of a single end organ". J Physiol. 61 (2): 151–171. doi:10.1113/jphysiol.1926.sp002281. PMC 1514782. PMID 16993780.
Forrest MD (2014). "Intracellular Calcium Dynamics Permit a Purkinje Neuron Model to Perform Toggle and Gain Computations Upon its Inputs". Frontiers in Computational Neuroscience. 8: 86. doi:10.3389/fncom.2014.00086. PMC 4138505. PMID 25191262.
Forrest MD (December 2014). "The sodium-potassium pump is an information processing element in brain computation". Frontiers in Physiology. 5 (472): 472. doi:10.3389/fphys.2014.00472. PMC 4274886. PMID 25566080.
^ Gollisch, T.; Meister, M. (2008-02-22). "Rapid Neural Coding in the Retina with Relative Spike Latencies". Science. 319 (5866): 1108–1111. Bibcode:2008Sci...319.1108G. doi:10.1126/science.1149639. ISSN 0036-8075. PMID 18292344. S2CID 1032537.
^ Dayan, Peter; Abbott, L. F. (2001). Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Massachusetts Institute of Technology Press. ISBN 978-0-262-04199-7.
Butts DA, Weng C, Jin J, et al. (September 2007). "Temporal precision in the neural code and the timescales of natural vision". Nature. 449 (7158): 92–5. Bibcode:2007Natur.449...92B. doi:10.1038/nature06105. PMID 17805296. S2CID 4402057.
Singh & Levy, "A consensus layer V pyramidal neuron can sustain interpulse-interval coding ", PLoS ONE, 2017
J. Leo van Hemmen, TJ Sejnowski. 23 Problems in Systems Neuroscience. Oxford Univ. Press, 2006. p.143-158.
^ Theunissen, F; Miller, JP (1995). "Temporal Encoding in Nervous Systems: A Rigorous Definition". Journal of Computational Neuroscience. 2 (2): 149–162. doi:10.1007/bf00961885. PMID 8521284. S2CID 206786736.
^ Zador, Stevens, Charles, Anthony. "The enigma of the brain". © Current Biology 1995, Vol 5 No 12. Retrieved August 4, 2012.{{cite web}}: CS1 maint: multiple names: authors list (link)
Kostal L, Lansky P, Rospars JP (November 2007). "Neuronal coding and spiking randomness". Eur. J. Neurosci. 26 (10): 2693–701. doi:10.1111/j.1460-9568.2007.05880.x. PMID 18001270. S2CID 15367988.
Gupta, Nitin; Singh, Swikriti Saran; Stopfer, Mark (2016-12-15). "Oscillatory integration windows in neurons". Nature Communications. 7: 13808. Bibcode:2016NatCo...713808G. doi:10.1038/ncomms13808. ISSN 2041-1723. PMC 5171764. PMID 27976720.
Jolivet, Renaud; Rauch, Alexander; Lüscher, Hans-Rudolf; Gerstner, Wulfram (2006-08-01). "Predicting spike timing of neocortical pyramidal neurons by simple threshold models". Journal of Computational Neuroscience. 21 (1): 35–49. doi:10.1007/s10827-006-7074-5. ISSN 1573-6873. PMID 16633938. S2CID 8911457.
Geoffrois, E.; Edeline, J.M.; Vibert, J.F. (1994). "Learning by Delay Modifications". In Eeckman, Frank H. (ed.). Computation in Neurons and Neural Systems. Springer. pp. 133–8. ISBN 978-0-7923-9465-5.
Sjöström, Jesper, and Wulfram Gerstner. "Spike-timing dependent plasticity." Spike-timing dependent plasticity 35 (2010).
Gollisch, T.; Meister, M. (22 February 2008). "Rapid Neural Coding in the Retina with Relative Spike Latencies". Science. 319 (5866): 1108–1111. Bibcode:2008Sci...319.1108G. doi:10.1126/science.1149639. PMID 18292344. S2CID 1032537.
Wainrib, Gilles; Michèle, Thieullen; Khashayar, Pakdaman (7 April 2010). "Intrinsic variability of latency to first-spike". Biological Cybernetics. 103 (1): 43–56. doi:10.1007/s00422-010-0384-8. PMID 20372920. S2CID 7121609.
Victor, Johnathan D (2005). "Spike train metrics". Current Opinion in Neurobiology. 15 (5): 585–592. doi:10.1016/j.conb.2005.08.002. PMC 2713191. PMID 16140522.
Hallock, Robert M.; Di Lorenzo, Patricia M. (2006). "Temporal coding in the gustatory system". Neuroscience & Biobehavioral Reviews. 30 (8): 1145–1160. doi:10.1016/j.neubiorev.2006.07.005. PMID 16979239. S2CID 14739301.
Carleton, Alan; Accolla, Riccardo; Simon, Sidney A. (2010). "Coding in the mammalian gustatory system". Trends in Neurosciences. 33 (7): 326–334. doi:10.1016/j.tins.2010.04.002. PMC 2902637. PMID 20493563.
Wilson, Rachel I (2008). "Neural and behavioral mechanisms of olfactory perception". Current Opinion in Neurobiology. 18 (4): 408–412. doi:10.1016/j.conb.2008.08.015. PMC 2596880. PMID 18809492.
^ Karl Diesseroth, Lecture. "Personal Growth Series: Karl Diesseroth on Cracking the Neural Code." Google Tech Talks. November 21, 2008. https://www.youtube.com/watch?v=5SLdSbp6VjM
^ Han X, Qian X, Stern P, Chuong AS, Boyden ES. "Informational lesions: optical perturbations of spike timing and neural synchrony via microbial opsin gene fusions." Cambridge, Massachusetts: MIT Media Lad, 2009.
^ Montemurro, Marcelo A.; Rasch, Malte J.; Murayama, Yusuke; Logothetis, Nikos K.; Panzeri, Stefano (2008). "Phase-of-Firing Coding of Natural Visual Stimuli in Primary Visual Cortex". Current Biology. 18 (5): 375–380. doi:10.1016/j.cub.2008.02.023. PMID 18328702.
Fries P, Nikolić D, Singer W (July 2007). "The gamma cycle". Trends Neurosci. 30 (7): 309–16. doi:10.1016/j.tins.2007.05.005. PMID 17555828. S2CID 3070167.
Spike arrival times: A highly efficient coding scheme for neural networks Archived 2012-02-15 at the Wayback Machine, SJ Thorpe - Parallel processing in neural systems, 1990
^ Havenith MN, Yu S, Biederlack J, Chen NH, Singer W, Nikolić D (June 2011). "Synchrony makes neurons fire in sequence, and stimulus properties determine who is ahead". J. Neurosci. 31 (23): 8570–84. doi:10.1523/JNEUROSCI.2817-10.2011. PMC 6623348. PMID 21653861.
Wu S, Amari S, Nakahara H (May 2002). "Population coding and decoding in a neural field: a computational study". Neural Comput. 14 (5): 999–1026. doi:10.1162/089976602753633367. PMID 11972905. S2CID 1122223.
Maunsell JH, Van Essen DC (May 1983). "Functional properties of neurons in middle temporal visual area of the macaque monkey. I. Selectivity for stimulus direction, speed, and orientation". J. Neurophysiol. 49 (5): 1127–47. doi:10.1152/jn.1983.49.5.1127. PMID 6864242. S2CID 8708245.
"Intro to Sensory Motor Systems Ch. 38 page 766" (PDF). Archived from the original (PDF) on 2012-05-11. Retrieved 2014-02-03.
Science. 1986 Sep 26;233(4771):1416-9
Sachs, Murray B.; Young, Eric D. (November 1979). "Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory-nerve fibers". The Journal of the Acoustical Society of America. 66 (5): 1381–1403. Bibcode:1979ASAJ...66.1381Y. doi:10.1121/1.383532. PMID 500976.
Miller, M.I.; Sachs, M.B. (June 1984). "Representation of voice pitch in discharge patterns of auditory-nerve fibers". Hearing Research. 14 (3): 257–279. doi:10.1016/0378-5955(84)90054-6. PMID 6480513. S2CID 4704044.
Miller, M.I.; Sachs, M.B. (1983). "Representation of stop consonants in the discharge patterns of auditory-nerve fibrers". The Journal of the Acoustical Society of America. 74 (2): 502–517. Bibcode:1983ASAJ...74..502M. doi:10.1121/1.389816. PMID 6619427.
Hubel DH, Wiesel TN (October 1959). "Receptive fields of single neurones in the cat's striate cortex". J. Physiol. 148 (3): 574–91. doi:10.1113/jphysiol.1959.sp006308. PMC 1363130. PMID 14403679.
Schneidman, E; Berry, MJ; Segev, R; Bialek, W (2006), "Weak Pairwise Correlations Imply Strongly Correlated Network States in a Neural Population", Nature, 440 (7087): 1007–1012, arXiv:q-bio/0512013, Bibcode:2006Natur.440.1007S, doi:10.1038/nature04701, PMC 1785327, PMID 16625187
Amari, SL (2001), "Information Geometry on Hierarchy of Probability Distributions", IEEE Transactions on Information Theory, 47 (5): 1701–1711, CiteSeerX 10.1.1.46.5226, doi:10.1109/18.930911
Onken, A; Grünewälder, S; Munk, MHJ; Obermayer, K (2009), "Analyzing Short-Term Noise Dependencies of Spike-Counts in Macaque Prefrontal Cortex Using Copulas and the Flashlight Transformation", PLOS Comput Biol, 5 (11): e1000577, Bibcode:2009PLSCB...5E0577O, doi:10.1371/journal.pcbi.1000577, PMC 2776173, PMID 19956759
Johnson, KO (Jun 1980). "Sensory discrimination: neural processes preceding discrimination decision". J Neurophysiol. 43 (6): 1793–815. doi:10.1152/jn.1980.43.6.1793. PMID 7411183.
Panzeri; Schultz; Treves; Rolls (1999). "Correlations and the encoding of information in the nervous system". Proc Biol Sci. 266 (1423): 1001–12. doi:10.1098/rspb.1999.0736. PMC 1689940. PMID 10610508.
Merzenich, MM (Jun 1996). "Primary cortical representation of sounds by the coordination of action-potential timing". Nature. 381 (6583): 610–3. Bibcode:1996Natur.381..610D. doi:10.1038/381610a0. PMID 8637597. S2CID 4258853.
Rieke F, Warland D, de Ruyter van Steveninck R, Bialek W. Spikes: Exploring the Neural Code. Cambridge, Massachusetts: The MIT Press; 1999. ISBN 0-262-68108-0
Mathis A, Herz AV, Stemmler MB (July 2012). "Resolution of nested neuronal representations can be exponential in the number of neurons". Phys. Rev. Lett. 109 (1): 018103. Bibcode:2012PhRvL.109a8103M. doi:10.1103/PhysRevLett.109.018103. PMID 23031134.
Olshausen, Bruno A; Field, David J (1996). "Emergence of simple-cell receptive field properties by learning a sparse code for natural images" (PDF). Nature. 381 (6583): 607–609. Bibcode:1996Natur.381..607O. doi:10.1038/381607a0. PMID 8637596. S2CID 4358477. Archived from the original (PDF) on 2015-11-23. Retrieved 2016-03-29.
Gupta, N; Stopfer, M (6 October 2014). "A temporal channel for information in sparse sensory coding". Current Biology. 24 (19): 2247–56. doi:10.1016/j.cub.2014.08.021. PMC 4189991. PMID 25264257.
^ Rehn, Martin; Sommer, Friedrich T. (2007). "A network that uses few active neurones to code visual input predicts the diverse shapes of cortical receptive fields" (PDF). Journal of Computational Neuroscience. 22 (2): 135–146. doi:10.1007/s10827-006-0003-9. PMID 17053994. S2CID 294586.
Lee, Honglak; Battle, Alexis; Raina, Rajat; Ng, Andrew Y. (2006). "Efficient sparse coding algorithms" (PDF). Advances in Neural Information Processing Systems.
Olshausen, Bruno A.; Field, David J. (1997). "Sparse Coding with an Overcomplete Basis Set: A Strategy Employed by V1?". Vision Research. 37 (23): 3311–3325. doi:10.1016/s0042-6989(97)00169-7. PMID 9425546.
Zhang, Zhifeng; Mallat, Stephane G.; Davis, Geoffrey M. (July 1994). "Adaptive time-frequency decompositions". Optical Engineering. 33 (7): 2183–2192. Bibcode:1994OptEn..33.2183D. doi:10.1117/12.173207. ISSN 1560-2303.
Pati, Y. C.; Rezaiifar, R.; Krishnaprasad, P. S. (November 1993). "Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition". Proceedings of 27th Asilomar Conference on Signals, Systems and Computers. pp. 40–44 vol.1. CiteSeerX 10.1.1.348.5735. doi:10.1109/ACSSC.1993.342465. ISBN 978-0-8186-4120-6. S2CID 16513805.
Needell, D.; Tropp, J.A. (2009-05-01). "CoSaMP: Iterative signal recovery from incomplete and inaccurate samples". Applied and Computational Harmonic Analysis. 26 (3): 301–321. arXiv:0803.2392. doi:10.1016/j.acha.2008.07.002. ISSN 1063-5203. S2CID 1642637.
Kanerva, Pentti. Sparse distributed memory. MIT press, 1988
Vinje, WE; Gallant, JL (2000). "Sparse coding and decorrelation in primary visual cortex during natural vision". Science. 287 (5456): 1273–1276. Bibcode:2000Sci...287.1273V. CiteSeerX 10.1.1.456.2467. doi:10.1126/science.287.5456.1273. PMID 10678835.
Hromádka, T; Deweese, MR; Zador, AM (2008). "Sparse representation of sounds in the unanesthetized auditory cortex". PLOS Biol. 6 (1): e16. doi:10.1371/journal.pbio.0060016. PMC 2214813. PMID 18232737.
Crochet, S; Poulet, JFA; Kremer, Y; Petersen, CCH (2011). "Synaptic mechanisms underlying sparse coding of active touch". Neuron. 69 (6): 1160–1175. doi:10.1016/j.neuron.2011.02.022. PMID 21435560.
Ito, I; Ong, RCY; Raman, B; Stopfer, M (2008). "Sparse odor representation and olfactory learning". Nat Neurosci. 11 (10): 1177–1184. doi:10.1038/nn.2192. PMC 3124899. PMID 18794840.
A sparse memory is a precise memory. Oxford Science blog. 28 Feb 2014. http://www.ox.ac.uk/news/science-blog/sparse-memory-precise-memory
Lin, Andrew C., et al. "Sparse, decorrelated odor coding in the mushroom body enhances learned odor discrimination." Nature Neuroscience 17.4 (2014): 559-568.

Misplaced Pages