
Play top:
Play bottom:
Pitch is a perceptual property that allows sounds to be ordered on a frequency-related scale, or more commonly, pitch is the quality that makes it possible to judge sounds as "higher" and "lower" in the sense associated with musical melodies. Pitch is a major auditory attribute of musical tones, along with duration, loudness, and timbre.
Pitch may be quantified as a frequency, but pitch is not a purely objective physical property; it is a subjective psychoacoustical attribute of sound. Historically, the study of pitch and pitch perception has been a central problem in psychoacoustics, and has been instrumental in forming and testing theories of sound representation, processing, and perception in the auditory system.
Perception
Pitch and frequency
Pitch is an auditory sensation in which a listener assigns musical tones to relative positions on a musical scale based primarily on their perception of the frequency of vibration (audio frequency). Pitch is closely related to frequency, but the two are not equivalent. Frequency is an objective, scientific attribute which can be measured. Pitch is the subjective perception of a sound wave by the individual person, which cannot be directly measured. However, this does not necessarily mean that people will not agree on which notes are higher and lower.
The oscillations of sound waves can often be characterized in terms of frequency. Pitches are usually associated with, and thus quantified as, frequencies (in cycles per second, or hertz), by comparing the sounds being assessed against sounds with pure tones (ones with periodic, sinusoidal waveforms). Complex and aperiodic sound waves can often be assigned a pitch by this method.
According to the American National Standards Institute, pitch is the auditory attribute of sound allowing those sounds to be ordered on a scale from low to high. Since pitch is such a close proxy for frequency, it is almost entirely determined by how quickly the sound wave is making the air vibrate and has almost nothing to do with the intensity, or amplitude, of the wave. That is, "high" pitch means very rapid oscillation, and "low" pitch corresponds to slower oscillation. Despite that, the idiom relating vertical height to sound pitch is shared by most languages. At least in English, it is just one of many deep conceptual metaphors that involve up/down. The exact etymological history of the musical sense of high and low pitch is still unclear. There is evidence that humans do actually perceive that the source of a sound is slightly higher or lower in vertical space when the sound frequency is increased or reduced.
In most cases, the pitch of complex sounds such as speech and musical notes corresponds very nearly to the repetition rate of periodic or nearly-periodic sounds, or to the reciprocal of the time interval between repeating similar events in the sound waveform.
The pitch of complex tones can be ambiguous, meaning that two or more different pitches can be perceived, depending upon the observer. When the actual fundamental frequency can be precisely determined through physical measurement, it may differ from the perceived pitch because of overtones, also known as upper partials, harmonic or otherwise. A complex tone composed of two sine waves of 1000 and 1200 Hz may sometimes be heard as up to three pitches: two spectral pitches at 1000 and 1200 Hz, derived from the physical frequencies of the pure tones, and the combination tone at 200 Hz, corresponding to the repetition rate of the waveform. In a situation like this, the percept at 200 Hz is commonly referred to as the missing fundamental, which is often the greatest common divisor of the frequencies present.
Pitch depends to a lesser degree on the sound pressure level (loudness, volume) of the tone, especially at frequencies below 1,000 Hz and above 2,000 Hz. The pitch of lower tones gets lower as sound pressure increases. For instance, a tone of 200 Hz that is very loud seems one semitone lower in pitch than if it is just barely audible. Above 2,000 Hz, the pitch gets higher as the sound gets louder. These results were obtained in the pioneering works by S. Stevens and W. Snow. Later investigations, e.g. by A. Cohen, have shown that in most cases the apparent pitch shifts were not significantly different from pitch‐matching errors. When averaged, the remaining shifts followed the directions of Stevens's curves but were small (2% or less by frequency, i.e. not more than a semitone).
-
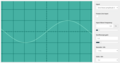 Lower pitches have lower frequency. C3, an octave below middle C. The frequency is half that of middle C (131 Hz). (Scale: 1 square is equal to 1 millisecond)
Lower pitches have lower frequency. C3, an octave below middle C. The frequency is half that of middle C (131 Hz). (Scale: 1 square is equal to 1 millisecond)
-
 Oscillogram of middle C (262 Hz) (pure tone)
Oscillogram of middle C (262 Hz) (pure tone)
-
 Higher pitches have higher frequency. Oscillogram of C5, an octave above middle C. The frequency is twice that of middle C (523 Hz).
Higher pitches have higher frequency. Oscillogram of C5, an octave above middle C. The frequency is twice that of middle C (523 Hz).
Theories of pitch perception
Theories of pitch perception try to explain how the physical sound and specific physiology of the auditory system work together to yield the experience of pitch. In general, pitch perception theories can be divided into place coding and temporal coding. Place theory holds that the perception of pitch is determined by the place of maximum excitation on the basilar membrane.
A place code, taking advantage of the tonotopy in the auditory system, must be in effect for the perception of high frequencies, since neurons have an upper limit on how fast they can phase-lock their action potentials. However, a purely place-based theory cannot account for the accuracy of pitch perception in the low and middle frequency ranges. Moreover, there is some evidence that some non-human primates lack auditory cortex responses to pitch despite having clear tonotopic maps in auditory cortex, showing that tonotopic place codes are not sufficient for pitch responses.
Temporal theories offer an alternative that appeals to the temporal structure of action potentials, mostly the phase-lock of action potentials to frequencies in a stimulus. The precise way this temporal structure helps code for pitch at higher levels is still debated, but the processing seems to be based on an autocorrelation of action potentials in the auditory nerve. However, it has long been noted that a neural mechanism that may accomplish a delay—a necessary operation of a true autocorrelation—has not been found. At least one model shows that a temporal delay is unnecessary to produce an autocorrelation model of pitch perception, appealing to phase shifts between cochlear filters; however, earlier work has shown that certain sounds with a prominent peak in their autocorrelation function do not elicit a corresponding pitch percept, and that certain sounds without a peak in their autocorrelation function nevertheless elicit a pitch. To be a more complete model, autocorrelation must therefore apply to signals that represent the output of the cochlea, as via auditory-nerve interspike-interval histograms. Some theories of pitch perception hold that pitch has inherent octave ambiguities, and therefore is best decomposed into a pitch chroma, a periodic value around the octave, like the note names in Western music—and a pitch height, which may be ambiguous, that indicates the octave the pitch is in.
Just-noticeable difference
The just-noticeable difference (jnd) (the threshold at which a change is perceived) depends on the tone's frequency content. Below 500 Hz, the jnd is about 3 Hz for sine waves, and 1 Hz for complex tones; above 1000 Hz, the jnd for sine waves is about 0.6% (about 10 cents). The jnd is typically tested by playing two tones in quick succession with the listener asked if there was a difference in their pitches. The jnd becomes smaller if the two tones are played simultaneously as the listener is then able to discern beat frequencies. The total number of perceptible pitch steps in the human hearing range is about 1,400; the total number of notes in the equal-tempered scale, from 16 to 16,000 Hz, is 120.
Aural illusions
The relative perception of pitch can be fooled, resulting in aural illusions. There are several of these, such as the tritone paradox, but most notably the Shepard scale, where a continuous or discrete sequence of specially formed tones can be made to sound as if the sequence continues ascending or descending forever.
Definite and indefinite pitch
Not all musical instruments make notes with a clear pitch. The unpitched percussion instruments (a class of percussion instruments) do not produce particular pitches. A sound or note of definite pitch is one where a listener can possibly (or relatively easily) discern the pitch. Sounds with definite pitch have harmonic frequency spectra or close to harmonic spectra.
A sound generated on any instrument produces many modes of vibration that occur simultaneously. A listener hears numerous frequencies at once. The vibration with the lowest frequency is called the fundamental frequency; the other frequencies are overtones. Harmonics are an important class of overtones with frequencies that are integer multiples of the fundamental. Whether or not the higher frequencies are integer multiples, they are collectively called the partials, referring to the different parts that make up the total spectrum.
A sound or note of indefinite pitch is one that a listener finds impossible or relatively difficult to identify as to pitch. Sounds with indefinite pitch do not have harmonic spectra or have altered harmonic spectra—a characteristic known as inharmonicity.
It is still possible for two sounds of indefinite pitch to clearly be higher or lower than one another. For instance, a snare drum sounds higher pitched than a bass drum though both have indefinite pitch, because its sound contains higher frequencies. In other words, it is possible and often easy to roughly discern the relative pitches of two sounds of indefinite pitch, but sounds of indefinite pitch do not neatly correspond to any specific pitch.
Pitch standards and standard pitch
Main article: Concert pitchA pitch standard (also concert pitch) is the conventional pitch reference that musical instruments in a group are tuned to for a performance. Concert pitch may vary from ensemble to ensemble, and has varied widely over musical history.

Problems playing this file? See media help.
Standard pitch is a more widely accepted convention. The A above middle C is usually set at 440 Hz (often written as "A = 440 Hz" or sometimes "A440"), although other frequencies, such as 442 Hz, are also often used as variants. Another standard pitch, the so-called Baroque pitch, has been set in the 20th century as A = 415 Hz—approximately an equal-tempered semitone lower than A440 to facilitate transposition. The Classical pitch can be set to either 427 Hz (about halfway between A415 and A440) or 430 Hz (also between A415 and A440 but slightly sharper than the quarter tone). And ensembles specializing in authentic performance set the A above middle C to 432 Hz or 435 Hz when performing repertoire from the Romantic era.
Transposing instruments have their origin in the variety of pitch standards. In modern times, they conventionally have their parts transposed into different keys from voices and other instruments (and even from each other). As a result, musicians need a way to refer to a particular pitch in an unambiguous manner when talking to each other.
For example, the most common type of clarinet or trumpet, when playing a note written in their part as C, sounds a pitch that is called B♭ on a non-transposing instrument like a violin (which indicates that at one time these wind instruments played at a standard pitch a tone lower than violin pitch). To refer to that pitch unambiguously, a musician calls it concert B♭, meaning, "the pitch that someone playing a non-transposing instrument like a violin calls B♭."
Labeling pitches
| This section needs additional citations for verification. Please help improve this article by adding citations to reliable sources in this section. Unsourced material may be challenged and removed. (December 2024) (Learn how and when to remove this message) |

Pitches are labeled using:
- Letters, as in Helmholtz pitch notation
- A combination of letters and numbers—as in scientific pitch notation, where notes are labelled upwards from C0, the 16 Hz C
- Numbers that represent the frequency in hertz (Hz), the number of cycles per second
For example, one might refer to the A above middle C as a′, A4, or 440 Hz. In standard Western equal temperament, the notion of pitch is insensitive to "spelling": the description "G4 double sharp" refers to the same pitch as A4; in other temperaments, these may be distinct pitches. Human perception of musical intervals is approximately logarithmic with respect to fundamental frequency: the perceived interval between the pitches "A220" and "A440" is the same as the perceived interval between the pitches A440 and A880. Motivated by this logarithmic perception, music theorists sometimes represent pitches using a numerical scale based on the logarithm of fundamental frequency. For example, one can adopt the widely used MIDI standard to map fundamental frequency, f, to a real number, p, as follows.
This creates a linear pitch space in which octaves have size 12, semitones (the distance between adjacent keys on the piano keyboard) have size 1, and A440 is assigned the number 69. (See Frequencies of notes.) Distance in this space corresponds to musical intervals as understood by musicians. An equal-tempered semitone is subdivided into 100 cents. The system is flexible enough to include "microtones" not found on standard piano keyboards. For example, the pitch halfway between C (60) and C♯ (61) can be labeled 60.5.
The following table shows frequencies in Hertz for notes in various octaves, named according to the "German method" of octave nomenclature:
| Note | Sub-contra | Contra | Great | Small | One-lined | Two-lined | Three-lined | Four-lined | Five-lined |
|---|---|---|---|---|---|---|---|---|---|
| B♯/C | 16.35 | 32.70 | 65.41 | 130.81 | 261.63 | 523.25 | 1046.50 | 2093.00 | 4186.01 |
| C♯/D♭ | 17.32 | 34.65 | 69.30 | 138.59 | 277.18 | 554.37 | 1108.73 | 2217.46 | 4434.92 |
| D | 18.35 | 36.71 | 73.42 | 146.83 | 293.66 | 587.33 | 1174.66 | 2349.32 | 4698.64 |
| D♯/E♭ | 19.45 | 38.89 | 77.78 | 155.56 | 311.13 | 622.25 | 1244.51 | 2489.02 | 4978.03 |
| E/F♭ | 20.60 | 41.20 | 82.41 | 164.81 | 329.63 | 659.26 | 1318.51 | 2637.02 | 5274.04 |
| E♯/F | 21.83 | 43.65 | 87.31 | 174.61 | 349.23 | 698.46 | 1396.91 | 2793.83 | 5587.65 |
| F♯/G♭ | 23.12 | 46.25 | 92.50 | 185.00 | 369.99 | 739.99 | 1479.98 | 2959.96 | 5919.91 |
| G | 24.50 | 49.00 | 98.00 | 196.00 | 392.00 | 783.99 | 1567.99 | 3135.96 | 6271.93 |
| G♯/A♭ | 25.96 | 51.91 | 103.83 | 207.65 | 415.30 | 830.61 | 1661.22 | 3322.44 | 6644.88 |
| A | 27.50 | 55.00 | 110.00 | 220.00 | 440.00 | 880.00 | 1760.00 | 3520.00 | 7040.00 |
| A♯/B♭ | 29.14 | 58.27 | 116.54 | 233.08 | 466.16 | 932.33 | 1864.66 | 3729.31 | 7458.62 |
| B/C♭ | 30.87 | 61.74 | 123.47 | 246.94 | 493.88 | 987.77 | 1975.53 | 3951.07 | 7902.13 |
Scales
The relative pitches of individual notes in a scale may be determined by one of a number of tuning systems. In the west, the twelve-note chromatic scale is the most common method of organization, with equal temperament now the most widely used method of tuning that scale. In it, the pitch ratio between any two successive notes of the scale is exactly the twelfth root of two (or about 1.05946). In well-tempered systems (as used in the time of Johann Sebastian Bach, for example), different methods of musical tuning were used.
In almost all of these systems interval of the octave doubles the frequency of a note; for example, an octave above A440 is 880 Hz. If however the first overtone is sharp due to inharmonicity, as in the extremes of the piano, tuners resort to octave stretching.
Other musical meanings of pitch
In atonal, twelve tone, or musical set theory, a "pitch" is a specific frequency while a pitch class is all the octaves of a frequency. In many analytic discussions of atonal and post-tonal music, pitches are named with integers because of octave and enharmonic equivalency (for example, in a serial system, C♯ and D♭ are considered the same pitch, while C4 and C5 are functionally the same, one octave apart).
Discrete pitches, rather than continuously variable pitches, are virtually universal, with exceptions including "tumbling strains" and "indeterminate-pitch chants". Gliding pitches are used in most cultures, but are related to the discrete pitches they reference or embellish.
See also
- 3rd bridge (harmonic resonance based on equal string divisions)
- Absolute pitch
- Diplacusis
- Eight foot pitch
- Harmonic pitch class profiles
- Just intonation
- Meantone temperament
- Music and mathematics
- Piano key frequencies
- Pitch circularity
- Pitch class
- Pitch detection algorithm
- Pitch of brass instruments
- Pitch shifter
- Pitch pipe
- Relative pitch
- Scale of vowels
- Vocal and instrumental pitch ranges
References
- Anssi Klapuri, "Introduction to Music Transcription", in Signal Processing Methods for Music Transcription, edited by Anssi Klapuri and Manuel Davy, 1–20 (New York: Springer, 2006): p. 8. ISBN 978-0-387-30667-4.
-
Plack, Christopher J.; Andrew J. Oxenham; Richard R. Fay, eds. (2005). Pitch: Neural Coding and Perception. New York: Springer. ISBN 978-0-387-23472-4.
For the purposes of this book we decided to take a conservative approach, and to focus on the relationship between pitch and musical melodies. Following the earlier ASA definition, we define pitch as 'that attribute of sensation whose variation is associated with musical melodies.' Although some might find this too restrictive, an advantage of this definition is that it provides a clear procedure for testing whether or not a stimulus evokes a pitch, and a clear limitation on the range of stimuli that we need to consider in our discussions.
- Roy D. Patterson; Etienne Gaudrain & Thomas C. Walters (2010). "The Perception of Family and Register in Musical Tones". In Mari Riess Jones; Richard R. Fay & Arthur N. Popper (eds.). Music Perception. Springer. pp. 37–38. ISBN 978-1-4419-6113-6.
- ^ Hartmann, William Morris (1997). Signals, Sound, and Sensation. Springer. pp. 145, 284, 287. ISBN 978-1-56396-283-7.
- ^ Plack, Christopher J.; Andrew J. Oxenham; Richard R. Fay, eds. (2005). Pitch: Neural Coding and Perception. Springer. ISBN 978-0-387-23472-4.
- Robert A. Dobie & Susan B. Van Hemel (2005). Hearing Loss: Determining Eligibility for Social Security Benefits. National Academies Press. pp. 50–51. ISBN 978-0-309-09296-8.
- ^ E. Bruce Goldstein (2001). Blackwell Handbook of Perception (4th ed.). Wiley-Blackwell. p. 381. ISBN 978-0-631-20683-5.
- ^ Richard Lyon & Shihab Shamma (1996). "Auditory Representation of Timbre and Pitch". In Harold L. Hawkins & Teresa A. McMullen (eds.). Auditory Computation. Springer. pp. 221–23. ISBN 978-0-387-97843-7.
- ^ Carroll C. Pratt, "The Spatial Character of High and Low Tones", Journal of Experimental Psychology 13 (1930): 278–85.
- Schwartz, David A.; Dale Purves (May 2004). "Pitch Is Determined by Naturally Occurring Periodic Sounds". Hearing Research. 194 (1–2): 31–46. doi:10.1016/j.heares.2004.01.019. PMID 15276674. S2CID 40608136.
- ^ Olson, Harry F. (1967). Music, Physics and Engineering. Dover Publications. pp. 171, 248–251. ISBN 978-0-486-21769-7.
- Stevens S. S. The relation of pitch to intensity//J. Acoust. Soc. Amer. 1935. Vol. 6. p. 150–154.
- Snow W. B. (1936) Change of Pitch with Loudness at Low Frequencies. J. Acoust. Soc. Am/ 8:14–19.
- Cohen, A. (1961). Further investigation of the effects of intensity upon the pitch of pure tones. Journal of the Acoustical Society of America, 33, 1363–1376. https://dx.doi.org/10.1121/1.1908441
- Norman-Haignere, S.V.; Kanwisher, N.G.; McDermott, J.; Conway, B.R. (10 June 2019). "Divergence in the functional organization of human and macaque auditory cortex revealed by fMRI responses to harmonic tones". Nature Neuroscience. 22 (7): 1057–1060. doi:10.1038/s41593-019-0410-7. ISSN 1097-6256. PMC 6592717. PMID 31182868.
- Cariani, P.A.; Delgutte, B. (September 1996). "Neural Correlates of the Pitch of Complex Tones. I. Pitch and Pitch Salience" (PDF). Journal of Neurophysiology. 76 (3): 1698–1716. doi:10.1152/jn.1996.76.3.1698. PMID 8890286. Retrieved 13 November 2012.
- Cheveigné, A. de; Pressnitzer, D. (June 2006). "The Case of the Missing Delay Lines: Synthetic Delays Obtained by Cross-channel Phase Interaction" (PDF). Journal of the Acoustical Society of America. 119 (6): 3908–3918. Bibcode:2006ASAJ..119.3908D. doi:10.1121/1.2195291. PMID 16838534. Retrieved 13 November 2012.
- Kaernbach, C.; Demany, L. (October 1998). "Psychophysical Evidence Against the Autocorrelation Theory of Auditory Temporal Processing". Journal of the Acoustical Society of America. 104 (4): 2298–2306. Bibcode:1998ASAJ..104.2298K. doi:10.1121/1.423742. PMID 10491694.
- ^ Pressnitzer, D.; Cheveigné, A. de; Winter, I.M. (January 2002). "Perceptual Pitch Shift for Sounds with Similar Waveform Autocorrelation". Acoustics Research Letters Online. 3 (1): 1–6. doi:10.1121/1.1416671.
- Burns, E.M.; Viemeister, N. F. (October 1976). "Nonspectral Pitch". Journal of the Acoustical Society of America. 60 (4): 863–69. Bibcode:1976ASAJ...60..863B. doi:10.1121/1.381166.
- Fitzgerald, M. B.; Wright, B. (December 2005). "A Perceptual Learning Investigation of the Pitch Elicited by Amplitude-Modulated Noise". Journal of the Acoustical Society of America. 118 (6): 3794–3803. Bibcode:2005ASAJ..118.3794F. doi:10.1121/1.2074687. PMID 16419824.
- Birger Kollmeier; Thomas Brand & B. Meyer (2008). "Perception of Speech and Sound". In Jacob Benesty; M. Mohan Sondhi & Yiteng Huang (eds.). Springer Handbook of Speech Processing. Springer. p. 65. ISBN 978-3-540-49125-5.
- Levitin, Daniel (2007). This Is Your Brain on Music. New York: Penguin Group. p. 40. ISBN 978-0-452-28852-2.
The one with the slowest vibration rate—the one lowest in pitch—is referred to as the fundamental frequency, and the others are collectively called overtones.
- The Concise Grove Dictionary of Music: Hermann von Helmholtz, Oxford University Press (1994), Answers.com. Retrieved 3 August 2007.
- Helmholtz, Hermann (1885). On the Sensations of Tone (English Translation). Cosimo. p. 15. ISBN 9781602066397.
- Sachs, C. and Kunst, J. (1962). In The Wellsprings of Music, edited by J. Kunst. The Hague: Marinus Nijhoff. Cited in Burns (1999).
- Malm, W.P. (1967). Music Cultures of the Pacific, the Near East, and Asia. Englewood Cliffs, NJ: Prentice-Hall. Cited in Burns (1999).
- Burns, Edward M. (1999). "Intervals, Scales, and Tuning", The Psychology of Music, second edition. Deutsch, Diana, ed. San Diego: Academic Press. ISBN 0-12-213564-4.
Further reading
- Moore, B.C. & Glasberg, B.R. (1986) "Thresholds for Hearing Mistuned Partials as Separate Tones in Harmonic Complexes". Journal of the Acoustical Society of America, 80, 479–83.
- Parncutt, R. (1989). Harmony: A Psychoacoustical Approach. Berlin: Springer-Verlag, 1989.
- Schneider, P.; Sluming, V.; Roberts, N.; Scherg, M.; Goebel, R.; Specht, H.-J.; Dosch, H.G.; Bleeck, S.; Stippich, C.; Rupp, A. (2005). "Structural and Functional Asymmetry of Lateral Heschl's Gyrus Reflects Pitch Perception Preference". Nat. Neurosci. 8, 1241–47.
- Terhardt, E., Stoll, G. and Seewann, M. (1982). "Algorithm for Extraction of Pitch and Pitch Salience from Complex Tonal Signals". Journal of the Acoustical Society of America, 71, 679–88.
External links
| Melody | |
|---|---|
| Musical notation | |
|---|---|
| Staff | |
| Musical notes | |
| Articulation | |
| Sheet music | |
| Other systems | |
| Related | |
| Harmony | ||
|---|---|---|
| Timbre | |
|---|---|
| Mental processes | |
|---|---|
| Cognition | |
| Perception | |
| Memory | |
| Other | |
