Misplaced Pages

The active laser medium (also called a gain medium or lasing medium) is the source of optical gain within a laser. The gain results from the stimulated emission of photons through electronic or molecular transitions to a lower energy state from a higher energy state previously populated by a pump source.

Examples of active laser media include:

• Certain crystals, typically doped with rare-earth ions (e.g. neodymium, ytterbium, or erbium) or transition metal ions (titanium or chromium); most often yttrium aluminium garnet (Y₃Al₅O₁₂), yttrium orthovanadate (YVO₄), or sapphire (Al₂O₃); and not often caesium cadmium bromide (CsCdBr₃) (solid-state lasers)
• Glasses, e.g. silicate or phosphate glasses, doped with laser-active ions;
• Gases, e.g. mixtures of helium and neon (HeNe), nitrogen, argon, krypton, carbon monoxide, carbon dioxide, or metal vapors; (gas lasers)
• Semiconductors, e.g. gallium arsenide (GaAs), indium gallium arsenide (InGaAs), or gallium nitride (GaN).
• Liquids, in the form of dye solutions as used in dye lasers.

In order to fire a laser, the active gain medium must be changed into a state in which population inversion occurs. The preparation of this state requires an external energy source and is known as laser pumping. Pumping may be achieved with electrical currents (e.g. semiconductors, or gases via high-voltage discharges) or with light, generated by discharge lamps or by other lasers (semiconductor lasers). More exotic gain media can be pumped by chemical reactions, nuclear fission, or with high-energy electron beams.

Example of a model of gain medium

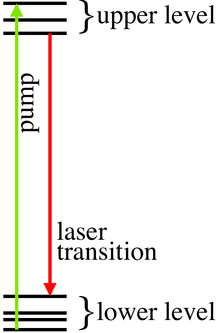
The simplest model of optical gain in real systems includes just two, energetically well separated, groups of sub-levels. Within each sub-level group, fast transitions ensure that thermal equilibrium is reached quickly. Stimulated emissions between upper and lower groups, essential for gain, require the upper levels to be more populated than the corresponding lower ones. This situation is called population-inversion. It is more readily achieved if unstimulated transition rates between the two groups are slow, i.e. the upper levels are metastable. Population inversions are more easily produced when only the lowest sublevels are occupied, requiring either low temperatures or well energetically split groups.

In the case of amplification of optical signals, the lasing frequency is called signal frequency. If the externally provided energy required for the signal's amplification is optical, it would necessarily be at the same or higher pump frequency.

Cross-sections

The simple medium can be characterized with effective cross-sections of absorption and emission at frequencies ${\displaystyle ~\omega _{\rm {p}}~}$ and ${\displaystyle ~\omega _{\rm {s}}}$.

• Have ${\displaystyle ~N~}$ be concentration of active centers in the solid-state lasers.
• Have ${\displaystyle ~N_{1}~}$ be concentration of active centers in the ground state.
• Have ${\displaystyle ~N_{2}~}$ be concentration of excited centers.
• Have ${\displaystyle ~N_{1}+N_{2}=N}$.

The relative concentrations can be defined as ${\displaystyle ~n_{1}=N_{1}/N~}$ and ${\displaystyle ~n_{2}=N_{2}/N}$.

The rate of transitions of an active center from the ground state to the excited state can be expressed like this: ${\displaystyle ~W_{\rm {u}}={\frac {I_{\rm {p}}\sigma _{\rm {ap}}}{\hbar \omega _{\rm {p}}}}+{\frac {I_{\rm {s}}\sigma _{\rm {as}}}{\hbar \omega _{\rm {s}}}}~}$.

While the rate of transitions back to the ground state can be expressed like: ${\displaystyle ~W_{\rm {d}}={\frac {I_{\rm {p}}\sigma _{\rm {ep}}}{\hbar \omega _{\rm {p}}}}+{\frac {I_{\rm {s}}\sigma _{\rm {es}}}{\hbar \omega _{\rm {s}}}}+{\frac {1}{\tau }}~}$, where ${\displaystyle ~\sigma _{\rm {as}}~}$ and ${\displaystyle ~\sigma _{\rm {ap}}~}$ are effective cross-sections of absorption at the frequencies of the signal and the pump, ${\displaystyle ~\sigma _{\rm {es}}~}$ and ${\displaystyle ~\sigma _{\rm {ep}}~}$ are the same for stimulated emission, and ${\displaystyle ~{\frac {1}{\tau }}~}$ is rate of the spontaneous decay of the upper level.

Then, the kinetic equation for relative populations can be written as follows:

${\displaystyle ~{\frac {{\rm {d}}n_{2}}{{\rm {d}}t}}=W_{\rm {u}}n_{1}-W_{\rm {d}}n_{2}}$,

${\displaystyle ~{\frac {{\rm {d}}n_{1}}{{\rm {d}}t}}=-W_{\rm {u}}n_{1}+W_{\rm {d}}n_{2}~}$ However, these equations keep ${\displaystyle ~n_{1}+n_{2}=1~}$.

The absorption ${\displaystyle ~A~}$ at the pump frequency and the gain ${\displaystyle ~G~}$ at the signal frequency can be written as follows:

${\displaystyle ~A=N_{1}\sigma _{\rm {pa}}-N_{2}\sigma _{\rm {pe}}~}$ and ${\displaystyle ~G=N_{2}\sigma _{\rm {se}}-N_{1}\sigma _{\rm {sa}}~}$.

Steady-state solution

In many cases the gain medium works in a continuous-wave or quasi-continuous regime, causing the time derivatives of populations to be negligible.

The steady-state solution can be written:

${\displaystyle ~n_{2}={\frac {W_{\rm {u}}}{W_{\rm {u}}+W_{\rm {d}}}}~}$, ${\displaystyle ~n_{1}={\frac {W_{\rm {d}}}{W_{\rm {u}}+W_{\rm {d}}}}.}$

The dynamic saturation intensities can be defined:

${\displaystyle ~I_{\rm {po}}={\frac {\hbar \omega _{\rm {p}}}{(\sigma _{\rm {ap}}+\sigma _{\rm {ep}})\tau }}~}$, ${\displaystyle ~I_{\rm {so}}={\frac {\hbar \omega _{\rm {s}}}{(\sigma _{\rm {as}}+\sigma _{\rm {es}})\tau }}~}$.

The absorption at strong signal: ${\displaystyle ~A_{0}={\frac {ND}{\sigma _{\rm {as}}+\sigma _{\rm {es}}}}~}$.

The gain at strong pump: ${\displaystyle ~G_{0}={\frac {ND}{\sigma _{\rm {ap}}+\sigma _{\rm {ep}}}}~}$, where ${\displaystyle ~D=\sigma _{\rm {pa}}\sigma _{\rm {se}}-\sigma _{\rm {pe}}\sigma _{\rm {sa}}~}$ is determinant of cross-section.

Gain never exceeds value ${\displaystyle ~G_{0}~}$, and absorption never exceeds value ${\displaystyle ~A_{0}U~}$.

At given intensities ${\displaystyle ~I_{\rm {p}}~}$, ${\displaystyle ~I_{\rm {s}}~}$ of pump and signal, the gain and absorption can be expressed as follows:

${\displaystyle ~A=A_{0}{\frac {U+s}{1+p+s}}~}$, ${\displaystyle ~G=G_{0}{\frac {p-V}{1+p+s}}~}$,

where ${\displaystyle ~p=I_{\rm {p}}/I_{\rm {po}}~}$, ${\displaystyle ~s=I_{\rm {s}}/I_{\rm {so}}~}$, ${\displaystyle ~U={\frac {(\sigma _{\rm {as}}+\sigma _{\rm {es}})\sigma _{\rm {ap}}}{D}}~}$, ${\displaystyle ~V={\frac {(\sigma _{\rm {ap}}+\sigma _{\rm {ep}})\sigma _{\rm {as}}}{D}}~}$ .

Identities

The following identities take place: ${\displaystyle U-V=1~}$, ${\displaystyle ~A/A_{0}+G/G_{0}=1~.\ }$

The state of gain medium can be characterized with a single parameter, such as population of the upper level, gain or absorption.

Efficiency of the gain medium

The efficiency of a gain medium can be defined as ${\displaystyle ~E={\frac {I_{\rm {s}}G}{I_{\rm {p}}A}}~}$.

Within the same model, the efficiency can be expressed as follows: ${\displaystyle ~E={\frac {\omega _{\rm {s}}}{\omega _{\rm {p}}}}{\frac {1-V/p}{1+U/s}}~}$.

For efficient operation, both intensities—pump and signal—should exceed their saturation intensities: ${\displaystyle ~{\frac {p}{V}}\gg 1~}$, and ${\displaystyle ~{\frac {s}{U}}\gg 1~}$.

The estimates above are valid for a medium uniformly filled with pump and signal light. Spatial hole burning may slightly reduce the efficiency because some regions are pumped well, but the pump is not efficiently withdrawn by the signal in the nodes of the interference of counter-propagating waves.

See also

• Population inversion
• Laser construction
• Laser science
• List of laser articles
• List of laser types

References and notes

1. Hecht, Jeff. The Laser Guidebook: Second Edition. McGraw-Hill, 1992. (Chapter 22)
2. Hecht, Chapter 22
3. Hecht, Chapters 7-15
4. Hecht, Chapters 18–21
5. F. J. Duarte and L. W. Hillman (Eds.), Dye Laser Principles (Academic, New York, 1990).
6. F. P. Schäfer (Ed.), Dye Lasers, 2nd Edition (Springer-Verlag, Berlin, 1990).
7. McArthur, D. A.; Tollefsrud, P. B. (15 February 1975). "Observation of laser action in CO gas excited only by fission fragments". Applied Physics Letters. 26 (4): 187–190. Bibcode:1975ApPhL..26..187M. doi:10.1063/1.88110.
8. Encyclopedia of laser physics and technology
9. D.Kouznetsov; J.F.Bisson; K.Takaichi; K.Ueda (2005). "Single-mode solid-state laser with short wide unstable cavity". JOSA B. 22 (8): 1605–1619. Bibcode:2005JOSAB..22.1605K. doi:10.1364/JOSAB.22.001605.

External links

• Gain media Encyclopedia of Laser Physics and Technology

• Laser gain media
• Laser science