Misplaced Pages

Leidenfrost effect

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Leidenfrost point) Physical phenomenon
Leidenfrost droplet
Demonstration of the Leidenfrost effect
Leidenfrost effect of a single drop of water

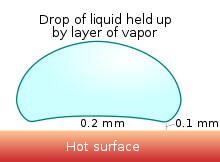
The Leidenfrost effect is a physical phenomenon in which a liquid, close to a solid surface of another body that is significantly hotter than the liquid's boiling point, produces an insulating vapor layer that keeps the liquid from boiling rapidly. Because of this repulsive force, a droplet hovers over the surface, rather than making physical contact with it. The effect is named after the German doctor Johann Gottlob Leidenfrost, who described it in A Tract About Some Qualities of Common Water.

This is most commonly seen when cooking, when drops of water are sprinkled onto a hot pan. If the pan's temperature is at or above the Leidenfrost point, which is approximately 193 °C (379 °F) for water, the water skitters across the pan and takes longer to evaporate than it would take if the water droplets had been sprinkled onto a cooler pan.

Details

A video clip demonstrating the Leidenfrost effect
Excitation of normal modes in a drop of water during the Leidenfrost effect

The effect can be seen as drops of water are sprinkled onto a pan at various times as it heats up. Initially, as the temperature of the pan is just below 100 °C (212 °F), the water flattens out and slowly evaporates, or if the temperature of the pan is well below 100 °C (212 °F), the water stays liquid. As the temperature of the pan rises above 100 °C (212 °F), the water droplets hiss when touching the pan, and these droplets evaporate quickly. When the temperature exceeds the Leidenfrost point, the Leidenfrost effect appears. On contact with the pan, the water droplets bunch up into small balls of water and skitter around, lasting much longer than when the temperature of the pan was lower. This effect works until a much higher temperature causes any further drops of water to evaporate too quickly to cause this effect.

The effect happens because, at temperatures at or above the Leidenfrost point, the bottom part of the water droplet vaporizes immediately on contact with the hot pan. The resulting gas suspends the rest of the water droplet just above it, preventing any further direct contact between the liquid water and the hot pan. As steam has much poorer thermal conductivity than the metal pan, further heat transfer between the pan and the droplet is slowed down dramatically. This also results in the drop being able to skid around the pan on the layer of gas just under it.

Behavior of water on a hot plate. Graph shows heat transfer (flux) vs temperature. Leidenfrost effect occurs after transition boiling.

The temperature at which the Leidenfrost effect appears is difficult to predict. Even if the volume of the drop of liquid stays the same, the Leidenfrost point may be quite different, with a complicated dependence on the properties of the surface, as well as any impurities in the liquid. Some research has been conducted into a theoretical model of the system, but it is quite complicated.

The effect was also described by the Victorian steam boiler designer, William Fairbairn, in reference to its effect on massively reducing heat transfer from a hot iron surface to water, such as within a boiler. In a pair of lectures on boiler design, he cited the work of Pierre Hippolyte Boutigny (1798–1884) and Professor Bowman of King's College, London, in studying this. A drop of water that was vaporized almost immediately at 168 °C (334 °F) persisted for 152 seconds at 202 °C (396 °F). Lower temperatures in a boiler firebox might evaporate water more quickly as a result; compare Mpemba effect. An alternative approach was to increase the temperature beyond the Leidenfrost point. Fairbairn considered this, too, and may have been contemplating the flash steam boiler, but considered the technical aspects insurmountable for the time.

The Leidenfrost point may also be taken to be the temperature for which the hovering droplet lasts longest.

It has been demonstrated that it is possible to stabilize the Leidenfrost vapor layer of water by exploiting superhydrophobic surfaces. In this case, once the vapor layer is established, cooling never collapses the layer, and no nucleate boiling occurs; the layer instead slowly relaxes until the surface is cooled.

Droplets of different liquids with different boiling temperatures will also exhibit a Leidenfrost effect with respect to each other and repel each other.

The Leidenfrost effect has been used for the development of high sensitivity ambient mass spectrometry. Under the influence of the Leidenfrost condition, the levitating droplet does not release molecules, and the molecules are enriched inside the droplet. At the last moment of droplet evaporation, all the enriched molecules release in a short time period and thereby increase the sensitivity.

A heat engine based on the Leidenfrost effect has been prototyped; it has the advantage of extremely low friction.

The effect also applies when the surface is at room temperature but the liquid is cryogenic, allowing liquid nitrogen droplets to harmlessly roll off exposed skin. Conversely, the inverse Leidenfrost effect lets drops of relatively warm liquid levitate on a bath of liquid nitrogen.

Leidenfrost point

A water droplet experiencing Leidenfrost effect on a hot stove plate

The Leidenfrost point signifies the onset of stable film boiling. It represents the point on the boiling curve where the heat flux is at the minimum and the surface is completely covered by a vapor blanket. Heat transfer from the surface to the liquid occurs by conduction and radiation through the vapour. In 1756, Leidenfrost observed that water droplets supported by the vapor film slowly evaporate as they move about on the hot surface. As the surface temperature is increased, radiation through the vapor film becomes more significant and the heat flux increases with increasing excess temperature.

The minimum heat flux for a large horizontal plate can be derived from Zuber's equation,

q A m i n = C h f g ρ v [ σ g ( ρ L − ρ v ) ( ρ L + ρ v ) 2 ] 1 ╱ 4 {\displaystyle {{\frac {q}{A}}_{min}}=C{{h}_{fg}}{{\rho }_{v}}{{\left}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}}

where the properties are evaluated at saturation temperature. Zuber's constant, C {\displaystyle C} , is approximately 0.09 for most fluids at moderate pressures.

Heat transfer correlations

The heat transfer coefficient may be approximated using Bromley's equation,

h = C [ k v 3 ρ v g ( ρ L − ρ v ) ( h f g + 0.4 c p v ( T s − T s a t ) ) D o μ v ( T s − T s a t ) ] 1 ╱ 4 {\displaystyle h=C{{\left}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}}

where D o {\displaystyle {{D}_{o}}} is the outside diameter of the tube. The correlation constant C is 0.62 for horizontal cylinders and vertical plates, and 0.67 for spheres. Vapor properties are evaluated at film temperature.

For stable film boiling on a horizontal surface, Berenson has modified Bromley's equation to yield,

h = 0.425 [ k v f 3 ρ v f g ( ρ L − ρ v ) ( h f g + 0.4 c p v ( T s − T s a t ) ) μ v f ( T s − T s a t ) σ / g ( ρ L − ρ v ) ] 1 ╱ 4 {\displaystyle h=0.425{{\left}^{{}^{1}\!\!\diagup \!\!{}_{4}\;}}}

For vertical tubes, Hsu and Westwater have correlated the following equation,

h [ μ v 2 g ρ v ( ρ L − ρ v ) k v 3 ] 1 ╱ 3 = 0.0020 [ 4 m π D v μ v ] 0.6 {\displaystyle h{{\left}^{{}^{1}\!\!\diagup \!\!{}_{3}\;}}=0.0020{{\left}^{0.6}}}

where m is the mass flow rate in l b m / h r {\displaystyle l{{b}_{m}}/hr} at the upper end of the tube.

At excess temperatures above that at the minimum heat flux, the contribution of radiation becomes appreciable, and it becomes dominant at high excess temperatures. The total heat transfer coefficient is thus a combination of the two. Bromley has suggested the following equations for film boiling from the outer surface of horizontal tubes:

h 4 ╱ 3 = h c o n v 4 ╱ 3 + h r a d h 1 ╱ 3 {\displaystyle {{h}^{{}^{4}\!\!\diagup \!\!{}_{3}\;}}={{h}_{conv}}^{{}^{4}\!\!\diagup \!\!{}_{3}\;}+{{h}_{rad}}{{h}^{{}^{1}\!\!\diagup \!\!{}_{3}\;}}}

If h r a d < h c o n v {\displaystyle {{h}_{rad}}<{{h}_{conv}}} ,

h = h c o n v + 3 4 h r a d {\displaystyle h={{h}_{conv}}+{\frac {3}{4}}{{h}_{rad}}}

The effective radiation coefficient, h r a d {\displaystyle {{h}_{rad}}} can be expressed as,

h r a d = ε σ ( T s 4 − T s a t 4 ) ( T s − T s a t ) {\displaystyle {{h}_{rad}}={\frac {\varepsilon \sigma \left(T_{s}^{4}-T_{sat}^{4}\right)}{\left({{T}_{s}}-{{T}_{sat}}\right)}}}

where ε {\displaystyle \varepsilon } is the emissivity of the solid and σ {\displaystyle \sigma } is the Stefan–Boltzmann constant.

Pressure field in a Leidenfrost droplet

The equation for the pressure field in the vapor region between the droplet and the solid surface can be solved for using the standard momentum and continuity equations using a Boundary layer model. In this model for the sake of simplicity in solving, a linear temperature profile and a parabolic velocity profile are assumed within the vapor phase. The heat transfer within the vapor phase is assumed to be through conduction. With these approximations, the Navier–Stokes equations can be solved to get the pressure field.

Leidenfrost temperature and surface tension effects

The Leidenfrost temperature is the property of a given set of solid–liquid pair. The temperature of the solid surface beyond which the liquid undergoes the Leidenfrost phenomenon is termed the Leidenfrost temperature. Calculation of the Leidenfrost temperature involves the calculation of the minimum film boiling temperature of a fluid. Berenson obtained a relation for the minimum film boiling temperature from minimum heat flux arguments. While the equation for the minimum film boiling temperature, which can be found in the reference above, is quite complex, the features of it can be understood from a physical perspective. One critical parameter to consider is the surface tension. The proportional relationship between the minimum film boiling temperature and surface tension is to be expected, since fluids with higher surface tension need higher quantities of heat flux for the onset of nucleate boiling. Since film boiling occurs after nucleate boiling, the minimum temperature for film boiling should have a proportional dependence on the surface tension.

Henry developed a model for Leidenfrost phenomenon which includes transient wetting and microlayer evaporation. Since the Leidenfrost phenomenon is a special case of film boiling, the Leidenfrost temperature is related to the minimum film boiling temperature via a relation which factors in the properties of the solid being used. While the Leidenfrost temperature is not directly related to the surface tension of the fluid, it is indirectly dependent on it through the film boiling temperature. For fluids with similar thermophysical properties, the one with higher surface tension usually has a higher Leidenfrost temperature.

For example, for a saturated water–copper interface, the Leidenfrost temperature is 257 °C (495 °F). The Leidenfrost temperatures for glycerol and common alcohols are significantly smaller because of their lower surface tension values (density and viscosity differences are also contributing factors.)

Reactive Leidenfrost effect

Reactive Leidenfrost effect of cellulose on silica, 750 °C (1,380 °F)

Non-volatile materials were discovered in 2015 to also exhibit a 'reactive Leidenfrost effect', whereby solid particles were observed to float above hot surfaces and skitter around erratically. Detailed characterization of the reactive Leidenfrost effect was completed for small particles of cellulose (~0.5 mm) on high temperature polished surfaces by high speed photography. Cellulose was shown to decompose to short-chain oligomers which melt and wet smooth surfaces with increasing heat transfer associated with increasing surface temperature. Above 675 °C (1,247 °F), cellulose was observed to exhibit transition boiling with violent bubbling and associated reduction in heat transfer. Liftoff of the cellulose droplet (depicted at the right) was observed to occur above about 750 °C (1,380 °F), associated with a dramatic reduction in heat transfer.

High speed photography of the reactive Leidenfrost effect of cellulose on porous surfaces (macroporous alumina) was also shown to suppress the reactive Leidenfrost effect and enhance overall heat transfer rates to the particle from the surface. The new phenomenon of a 'reactive Leidenfrost (RL) effect' was characterized by a dimensionless quantity, (φRL= τconv/τrxn), which relates the time constant of solid particle heat transfer to the time constant of particle reaction, with the reactive Leidenfrost effect occurring for 10< φRL< 10. The reactive Leidenfrost effect with cellulose will occur in numerous high temperature applications with carbohydrate polymers, including biomass conversion to biofuels, preparation and cooking of food, and tobacco use.

The Leidenfrost effect has also been used as a means to promote chemical change of various organic liquids through their conversion by thermal decomposition into various products. Examples include decomposition of ethanol, diethyl carbonate, and glycerol.

In popular culture

In Jules Verne's 1876 book Michael Strogoff, the protagonist is saved from being blinded with a hot blade by evaporating tears.

In the 2009 season 7 finale of MythBusters, "Mini Myth Mayhem", the team demonstrated that a person can wet their hand and briefly dip it into molten lead without injury, using the Leidenfrost effect as the scientific basis.

See also

References

  1. Bernardin, John D.; Mudawar, Issam (2002). "A Cavity Activation and Bubble Growth Model of the Leidenfrost Point". Journal of Heat Transfer. 124 (5): 864–74. doi:10.1115/1.1470487.
  2. William Fairbairn (1851). Two Lectures: The Construction of Boilers, and on Boiler Explosions, with the means of prevention. Archived from the original on 2017-11-23.
  3. ^ Incropera; DeWitt; Bergman; Lavine (2006). Fundamentals of Heat and Mass Transfer (6th ed.). pp. 325–330. ISBN 0-471-45728-0.
  4. Vakarelski, Ivan U.; Patankar, Neelesh A.; Marston, Jeremy O.; Chan, Derek Y. C.; Thoroddsen, Sigurdur T. (2012). "Stabilization of Leidenfrost vapour layer by textured superhydrophobic surfaces". Nature. 489 (7415): 274–7. Bibcode:2012Natur.489..274V. doi:10.1038/nature11418. PMID 22972299. S2CID 4411432.
  5. Pacheco-Vázquez, F.; Ledesma-Alonso, R.; Palacio-Rangel, J. L.; Moreau, F. (12 November 2021). "Triple Leidenfrost Effect: Preventing Coalescence of Drops on a Hot Plate". Physical Review Letters. 127 (20): 204501. arXiv:2107.00438. Bibcode:2021PhRvL.127t4501P. doi:10.1103/PhysRevLett.127.204501. PMID 34860033. S2CID 235694660.
  6. Subhrakanti Saha; Lee Chuin Chen; Mridul Kanti Mandal; Kenzo Hiraoka (March 2013). "Leidenfrost Phenomenon-assisted Thermal Desorption (LPTD) and Its Application to Open Ion Sources at Atmospheric Pressure Mass Spectrometry". Journal of the American Society for Mass Spectrometry. 24 (3): 341–7. Bibcode:2013JASMS..24..341S. doi:10.1007/s13361-012-0564-y. PMID 23423791. S2CID 39368022.
  7. Wells, Gary G.; Ledesma-Aguilar, Rodrigio; McHale, Glen; Sefiane, Khellil (3 March 2015). "A sublimation heat engine". Nature Communications. 6: 6390. Bibcode:2015NatCo...6.6390W. doi:10.1038/ncomms7390. PMC 4366496. PMID 25731669.
  8. "Who What Why: How dangerous is liquid nitrogen?". BBC News. 8 October 2012.
  9. Adda-Bedia, M.; Kumar, S.; Lechenault, F.; Moulinet, S.; Schillaci, M.; Vella, D. (2016). "Inverse Leidenfrost Effect: Levitating Drops on Liquid Nitrogen". Langmuir. 32 (17): 4179–4188. doi:10.1021/acs.langmuir.6b00574. PMID 27054550. S2CID 21732968.
  10. ^ Welty, James R.; Wicks, Charles E.; Wilson, Robert E.; Rorrer, Gregory L. (2008). Fundamentals of Momentum, Heat and Mass transfer (5th ed.). John Wiley and Sons. p. 327. ISBN 978-0-470-12868-8.
  11. Carey, Van P. (2020). Liquid-Vapor Phase-Change Phenomena: An Introduction to the Thermophysics of Vaporization and Condensation Processes in Heat Transfer Equipment, Third Edition. CRC Press. doi:10.1201/9780429082221. ISBN 978-1-4987-1663-5. S2CID 243345698.
  12. Berenson, P. J. (1 August 1961). "Film-Boiling Heat Transfer From a Horizontal Surface". Journal of Heat Transfer. 83 (3): 351–356. doi:10.1115/1.3682280.
  13. Henry, R.E. (1972). "Correlation for the minimum wall superheat in film boiling". Transactions of the American Nuclear Society. 15 (1): 420–421. OCLC 4434452303. OSTI 4694181.
  14. ^ Teixeira, Andrew R.; Krumm, Christoph; Vinter, Katherine P.; Paulsen, Alex D.; Zhu, Cheng; Maduskar, Saurabh; Joseph, Kristeen E.; Greco, Katharine; Stelatto, Michael; Davis, Eric; Vincent, Brendon; Hermann, Richard; Suszynski, Wieslaw; Schmidt, Lanny D.; Fan, Wei; Rothstein, Jonathan P.; Dauenhauer, Paul J. (September 2015). "Reactive Liftoff of Crystalline Cellulose Particles". Scientific Reports. 5 (1): 11238. Bibcode:2015NatSR...511238T. doi:10.1038/srep11238. PMC 4460903. PMID 26057818.
  15. Avedisian, C. Thomas; Kuo, Wei-Chih; Tsang, Wing; Lowery, Adam (20 June 2018). "A Film Boiling Study of Ethanol Pyrolysis". Industrial & Engineering Chemistry Research. 57 (24): 8334–8340. doi:10.1021/acs.iecr.8b00770.
  16. Thomas Avedisian, C.; Kuo, Wei-Chih; Tsang, Wing; Lowery, Adam (1 June 2018). "High Temperature Thermal Decomposition of Diethyl Carbonate by Pool Film Boiling". Journal of Heat Transfer. 140 (6): 061501. doi:10.1115/1.4038572.
  17. Sharma, Pushan; Avedisian, C. Thomas; Brunson, Jordan D.; Tsang, Wing (1 August 2019). "Decomposition by film boiling heat transfer of glycerol". International Journal of Heat and Mass Transfer. 139: 873–880. Bibcode:2019IJHMT.139..873S. doi:10.1016/j.ijheatmasstransfer.2019.05.005. S2CID 191155524.
  18. Quéré, David (3 January 2013). "Leidenfrost Dynamics". Annual Review of Fluid Mechanics. 45 (1): 197–215. Bibcode:2013AnRFM..45..197Q. doi:10.1146/annurev-fluid-011212-140709.
  19. "Mini-Myth Mayhem". MythBusters. Season 7. Episode 136. December 28, 2009. Discovery Channel.

External links

States of matter (list)
State
Low energy
High energy
Other states
Phase transitions
Quantities
Concepts
Categories: