In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
Definition
Let △ABC be a plane triangle and let x : y : z be the trilinear coordinates of an arbitrary point in the plane of triangle △ABC.
A straight line in the plane of △ABC whose equation in trilinear coordinates has the form where the point with trilinear coordinates is a triangle center, is a central line in the plane of △ABC relative to △ABC.
Central lines as trilinear polars
The geometric relation between a central line and its associated triangle center can be expressed using the concepts of trilinear polars and isogonal conjugates.
Let be a triangle center. The line whose equation is is the trilinear polar of the triangle center X. Also the point is the isogonal conjugate of the triangle center X.
Thus the central line given by the equation is the trilinear polar of the isogonal conjugate of the triangle center
Construction of central lines

Let X be any triangle center of △ABC.
- Draw the lines AX, BX, CX and their reflections in the internal bisectors of the angles at the vertices A, B, C respectively.
- The reflected lines are concurrent and the point of concurrence is the isogonal conjugate Y of X.
- Let the cevians AY, BY, CY meet the opposite sidelines of △ABC at A', B', C' respectively. The triangle △A'B'C' is the cevian triangle of Y.
- The △ABC and the cevian triangle △A'B'C' are in perspective and let DEF be the axis of perspectivity of the two triangles. The line DEF is the trilinear polar of the point Y. DEF is the central line associated with the triangle center X.
Some named central lines
Let Xn be the nth triangle center in Clark Kimberling's Encyclopedia of Triangle Centers. The central line associated with Xn is denoted by Ln. Some of the named central lines are given below.

Central line associated with X1, the incenter: Antiorthic axis
The central line associated with the incenter X1 = 1 : 1 : 1 (also denoted by I) is This line is the antiorthic axis of △ABC.
- The isogonal conjugate of the incenter of △ABC is the incenter itself. So the antiorthic axis, which is the central line associated with the incenter, is the axis of perspectivity of △ABC and its incentral triangle (the cevian triangle of the incenter of △ABC).
- The antiorthic axis of △ABC is the axis of perspectivity of △ABC and the excentral triangle △I1I2I3 of △ABC.
- The triangle whose sidelines are externally tangent to the excircles of △ABC is the extangents triangle of △ABC. △ABC and its extangents triangle are in perspective and the axis of perspectivity is the antiorthic axis of △ABC.

Central line associated with X2, the centroid: Lemoine axis
The trilinear coordinates of the centroid X2 (also denoted by G) of △ABC are: So the central line associated with the centroid is the line whose trilinear equation is This line is the Lemoine axis, also called the Lemoine line, of △ABC.
- The isogonal conjugate of the centroid X2 is the symmedian point X6 (also denoted by K) having trilinear coordinates a : b : c. So the Lemoine axis of △ABC is the trilinear polar of the symmedian point of △ABC.
- The tangential triangle of △ABC is the triangle △TATBTC formed by the tangents to the circumcircle of △ABC at its vertices. △ABC and its tangential triangle are in perspective and the axis of perspectivity is the Lemoine axis of △ABC.
Central line associated with X3, the circumcenter: Orthic axis

The trilinear coordinates of the circumcenter X3 (also denoted by O) of △ABC are: So the central line associated with the circumcenter is the line whose trilinear equation is This line is the orthic axis of △ABC.
- The isogonal conjugate of the circumcenter X3 is the orthocenter X4 (also denoted by H) having trilinear coordinates sec A : sec B : sec C. So the orthic axis of △ABC is the trilinear polar of the orthocenter of △ABC. The orthic axis of △ABC is the axis of perspectivity of △ABC and its orthic triangle △HAHBHC. It is also the radical axis of the triangle's circumcircle and nine-point-circle.
Central line associated with X4, the orthocenter

The trilinear coordinates of the orthocenter X4 (also denoted by H) of △ABC are: So the central line associated with the circumcenter is the line whose trilinear equation is
- The isogonal conjugate of the orthocenter of a triangle is the circumcenter of the triangle. So the central line associated with the orthocenter is the trilinear polar of the circumcenter.
Central line associated with X5, the nine-point center

The trilinear coordinates of the nine-point center X5 (also denoted by N) of △ABC are: So the central line associated with the nine-point center is the line whose trilinear equation is
- The isogonal conjugate of the nine-point center of △ABC is the Kosnita point X54 of △ABC. So the central line associated with the nine-point center is the trilinear polar of the Kosnita point.
- The Kosnita point is constructed as follows. Let O be the circumcenter of △ABC. Let OA, OB, OC be the circumcenters of the triangles △BOC, △COA, △AOB respectively. The lines AOA, BOB, COC are concurrent and the point of concurrence is the Kosnita point of △ABC. The name is due to J Rigby.
Central line associated with X6, the symmedian point : Line at infinity
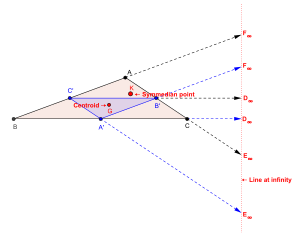
The trilinear coordinates of the symmedian point X6 (also denoted by K) of △ABC are: So the central line associated with the symmedian point is the line whose trilinear equation is
- This line is the line at infinity in the plane of △ABC.
- The isogonal conjugate of the symmedian point of △ABC is the centroid of △ABC. Hence the central line associated with the symmedian point is the trilinear polar of the centroid. This is the axis of perspectivity of the △ABC and its medial triangle.
Some more named central lines
Euler line
The Euler line of △ABC is the line passing through the centroid, the circumcenter, the orthocenter and the nine-point center of △ABC. The trilinear equation of the Euler line is This is the central line associated with the triangle center X647.
Nagel line
The Nagel line of △ABC is the line passing through the centroid, the incenter, the Spieker center and the Nagel point of △ABC. The trilinear equation of the Nagel line is This is the central line associated with the triangle center X649.
Brocard axis
The Brocard axis of △ABC is the line through the circumcenter and the symmedian point of △ABC. Its trilinear equation is This is the central line associated with the triangle center X523.
See also
References
- Kimberling, Clark (June 1994). "Central Points and Central Lines in the Plane of a Triangle". Mathematics Magazine. 67 (3): 163–187. doi:10.2307/2690608.
- ^ Kimberling, Clark (1998). Triangle Centers and Central Triangles. Winnipeg, Canada: Utilitas Mathematica Publishing, Inc. p. 285.
- Weisstein, Eric W. "Central Line". From MathWorld--A Wolfram Web Resource. Retrieved 24 June 2012.
- Kimberling, Clark. "Glossary : Encyclopedia of Triangle Centers". Archived from the original on 23 April 2012. Retrieved 24 June 2012.
- Weisstein, Eric W. "Trilinear Polar". From MathWorld--A Wolfram Web Resource. Retrieved 28 June 2012.
- Weisstein, Eric W. "Antiorthic Axis". From MathWorld--A Wolfram Web Resource. Retrieved 28 June 2012.
- Weisstein, Eric W. "Antiorthic Axis". From MathWorld--A Wolfram Web Resource. Retrieved 26 June 2012.
- Weisstein, Eric W. "Orthic Axis". From MathWorld--A Wolfram Web Resource.
- Weisstein, Eric W. "Nine-Point Center". From MathWorld--A Wolfram Web Resource. Retrieved 29 June 2012.
- Weisstein, Eric W. "Kosnita Point". From MathWorld--A Wolfram Web Resource. Retrieved 29 June 2012.
- Darij Grinberg (2003). "On the Kosnita Point and the Reflection Triangle" (PDF). Forum Geometricorum. 3: 105–111. Retrieved 29 June 2012.
- J. Rigby (1997). "Brief notes on some forgotten geometrical theorems". Mathematics & Informatics Quarterly. 7: 156–158.
 where the point with trilinear coordinates
where the point with trilinear coordinates
 is a triangle center, is a central line in the plane of △ABC relative to △ABC.
is a triangle center, is a central line in the plane of △ABC relative to △ABC.
 be a triangle center. The line whose equation is
be a triangle center. The line whose equation is
 is the
is the  is the
is the 
 This line is the antiorthic axis of △ABC.
This line is the antiorthic axis of △ABC.
 So the central line associated with the centroid is the line whose trilinear equation is
So the central line associated with the centroid is the line whose trilinear equation is
 This line is the Lemoine axis, also called the Lemoine line, of △ABC.
This line is the Lemoine axis, also called the Lemoine line, of △ABC.
 So the central line associated with the circumcenter is the line whose trilinear equation is
So the central line associated with the circumcenter is the line whose trilinear equation is
 This line is the orthic axis of △ABC.
This line is the orthic axis of △ABC.
 So the central line associated with the circumcenter is the line whose trilinear equation is
So the central line associated with the circumcenter is the line whose trilinear equation is

 So the central line associated with the nine-point center is the line whose trilinear equation is
So the central line associated with the nine-point center is the line whose trilinear equation is

 So the central line associated with the symmedian point is the line whose trilinear equation is
So the central line associated with the symmedian point is the line whose trilinear equation is

 This is the central line associated with the triangle center X647.
This is the central line associated with the triangle center X647.
 This is the central line associated with the triangle center X649.
This is the central line associated with the triangle center X649.
 This is the central line associated with the triangle center X523.
This is the central line associated with the triangle center X523.