In model checking, a branch of computer science, linear time properties are used to describe requirements of a model of a computer system. Example properties include "the vending machine does not dispense a drink until money has been entered" (a safety property) or "the computer program eventually terminates" (a liveness property). Fairness properties can be used to rule out unrealistic paths of a model. For instance, in a model of two traffic lights, the liveness property "both traffic lights are green infinitely often" may only be true under the unconditional fairness constraint "each traffic light changes colour infinitely often" (to exclude the case where one traffic light is "infinitely faster" than the other).
Formally, a linear time property is an ω-language over the power set of "atomic propositions". That is, the property contains sequences of sets of propositions, each sequence known as a "word". Every property can be rewritten as "P and Q both occur" for some safety property P and liveness property Q. An invariant for a system is something that is true or false for a particular state. Invariant properties describe an invariant that every reachable state of a model must satisfy, while persistence properties are of the form "eventually forever some invariant holds".
Temporal logics such as linear temporal logic describe types of linear time properties using formulae.
This article is about propositional linear-time properties and cannot handle predicates about program states, so it cannot define a property like: the current value of y determines the number of times that x toggles between 0 and 1 before termination. The more general formalism used in Safety and liveness properties can handle this.
Definition
Let AP be a set of atomic propositions. A word over (the power set of AP) is an infinite sequence of sets of propositions, such as (for the atomic propositions ). A linear time (LT) property over AP is a subset of i.e. a set of words. An example of an LT property over the set is "the set of words that contain a infinitely often". The word w is in this set, because a is contained in , which occurs infinitely often. A word not in this set is , as a only occurs once (in the first set).
An LT property is an ω-language over the alphabet (and vice versa).
We denote by pref(w) the finite prefixes of w (i.e. in the above case). The closure of an LT property P is:
Applications
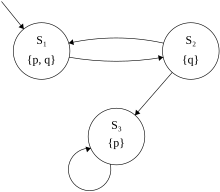
Using the theory of finite-state machines, a program or computer system can be modelled by a Kripke structure. LT properties then describe restrictions on the traces (outputs) of a Kripke structure. For instance, if two traffic lights at an intersection are represented by a Kripke structure then the atomic propositions may be the possible colours of each light and it may be desirable that the traces satisfy the LT property "the traffic lights cannot both be green at the same time" (to avoid car collisions).
If every trace of the Kripke structure TS is a trace of TS' then every LT property that TS' satisfies is satisfied by TS. This is useful in model checking to allow abstraction: if a simplified model of the system satisfies an LT property then the actual model of the system will satisfy it as well.
Classification of linear time properties
Safety properties
A safety property is informally of the form "a bad thing does not happen". For instance, if a system models an automated teller machine (ATM) then such a property is "money should not be dispensed unless a PIN has been entered". Formally, a safety property is an LT property such that any word that violates the property has a "bad prefix", for which no word with that prefix satisfies the property. That is,
In the ATM example, a minimal bad prefix is a finite set of steps carried out in which money is dispensed in the last step and a PIN is not entered at any step. To verify a safety property, it is sufficient to consider only the finite traces of a Kripke structure and check whether any such trace is a bad prefix.
An LT property P is a safety property if and only if .
Invariant properties
An invariant property is a type of safety property in which the condition only refers to the current state. For instance, the ATM example is not an invariant because we cannot tell whether the property is violated by seeing that the current state is "dispense money", only by seeing that the current state is "dispense money" and no previous state was "read PIN". An example of an invariant is the traffic light condition "the traffic lights cannot both be green at the same time" above. Another is "the variable x is never negative", in a model of a computer program.
Formally, an invariant is of the form:
for some propositional logic formula .
A Kripke structure satisfies an invariant if and only if every reachable state satisfies the invariant, which can be checked by a breadth-first search or depth-first search. Safety properties can be verified inductively using invariants.
Liveness properties
A liveness property is informally of the form "something good eventually happens". Formally, P is a liveness property if i.e. any finite string can be continued to a valid trace. An example of a liveness property is the previous LT property "the set of words that contain a infinitely often". No finite prefix of a word can prove that the word does not satisfy this property, as the word could continue on to have infinitely many as.
In terms of computer programs, useful liveness properties include "the program eventually terminates" and, in concurrent computing, "every process must eventually be served".
Persistence properties
A persistence property is a liveness property of the form "eventually forever ". That is, a property of the form:
Relation between safety and liveness properties
No LT property other than (the set of all words over ) is both a safety and a liveness property. Though not every property is a safety property or a liveness property (consider "a occurs exactly once"), every property is the intersection of a safety and a liveness property.
In topology, the set of all words can be equipped with the metric:
Then a safety property is a closed set and a liveness property is a dense set.
Fairness properties
Fairness properties are preconditions imposed on a system to rule out unrealistic traces. Unconditional fairness is of the form "every process gets its turn infinitely often". Strong fairness is of the form "every process gets its turn infinitely often if it is enabled infinitely often". Weak fairness is of the form "every process gets its turn infinitely often if it is continuously enabled from a particular point".
In some systems, a fairness constraint is defined by a set of states, and a "fair path" is one that passes through some state in the fairness constraint infinitely often. If there are multiple fairness constraints, then a fair path must pass infinitely often through one state per constraint. A program "fairly satisfies" an LT property P with respect to a set of fairness conditions if for every path, either the path fails a fairness condition or it satisfies P. That is, the property P is satisfied for all fair paths.
A fairness property is realizable for a Kripke structure if every reachable state has a fair path starting from that state. So long as a set of fairness conditions are realizable, they are irrelevant to safety properties.
Temporal logic
Temporal logics such as computation tree logic (CTL) can be used to specify some LT properties. All linear temporal logic (LTL) formulae are LT properties. By a counting argument, we see that any logic in which each formula is a finite string cannot represent all LT properties, as there must be countably many formulae but there are uncountably many LT properties.
Notes
- Baier & Katoen (2008), p. 126.
- Baier & Katoen (2008), pp. 97–98.
- Baier & Katoen (2008), pp. 97–99.
- Baier & Katoen (2008), p. 102.
- ^ Alpern & Schneider (1987).
- Baier & Katoen (2008), p. 109.
- ^ Finkbeiner & Torfah (2017), p. 4.
- Baier & Katoen (2008), p. 112.
- Baier & Katoen (2008), p. 113.
- ^ Baier & Katoen (2008), p. 105.
- Baier & Katoen (2008), pp. 105–106.
- Kern & Greenstreet (1999), p. 135.
- Baier & Katoen (2008), p. 119.
- D'Silva, Kroening & Weissenbacher (2008), p. 5.
- Baier & Katoen (2008), p. 197.
- Baier & Katoen (2008), p. 121.
- Baier & Katoen (2008), pp. 123–124.
- Baier & Katoen (2008), p. 124.
- Kern & Greenstreet (1999), pp. 131–132.
- Baier & Katoen (2008), pp. 126–127.
- Clarke, Grumberg & Kroening (2018), pp. 32–33.
- Baier & Katoen (2008), p. 132.
- Baier & Katoen (2008), pp. 137–139.
- Kern & Greenstreet (1999), p. 127.
References
- Alpern, B.; Schneider, F. B. (1987). "Recognizing safety and liveness". Distributed Computing. 2 (3): 117. CiteSeerX 10.1.1.20.5470. doi:10.1007/BF01782772. S2CID 9717112.
- Baier, Christel; Katoen, Joost-Pieter (2008). Principles of Model Checking. MIT Press. ISBN 9780262026499.
- Clarke, Edmund M.; Grumberg, Orna; Kroening, Daniel (2018). Model Checking. MIT Press. ISBN 9780262038836.
- D'Silva, Vijay; Kroening, Daniel; Weissenbacher, Georg (2008). "A Survey of Automated Techniques for Formal Software Verification". IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems. 27 (7): 1165–1178. doi:10.1109/TCAD.2008.923410. S2CID 8921624.
- Finkbeiner, Bernd; Torfah, Hazem (2017). "The Density of Linear-Time Properties". Lecture Notes in Computer Science. Automated Technology for Verification and Analysis. Vol. 10482. Springer.
- Kern, Christoph; Greenstreet, Mark R. (1999). "Formal Verification in Hardware Design: A Survey". ACM Transactions on Design Automation of Electronic Systems. 4 (2). Association for Computing Machinery. doi:10.1145/307988.307989. ISSN 1084-4309. S2CID 13994730.
Further reading
- Emerson, E. Allen (1990). "Temporal and modal logic". Handbook of Theoretical Computer Science. B.
- Pnueli, Amir (1986). "Applications of temporal logic to the specification and verification of reactive systems: A survey of current trends". In J. W. Bakker; W.-P. Roever; G. Rozenberg (eds.). Current Trends in Concurrency. Lecture Notes in Computer Science. Vol. 224. Springer. pp. 510–584. doi:10.1007/BFb0027047. ISBN 978-3-540-16488-3.
 (the
(the  (for the atomic propositions
(for the atomic propositions  ). A linear time (LT) property over AP is a subset of
). A linear time (LT) property over AP is a subset of  i.e. a set of words. An example of an LT property over the set
i.e. a set of words. An example of an LT property over the set  is "the set of words that contain a infinitely often". The word w is in this set, because a is contained in
is "the set of words that contain a infinitely often". The word w is in this set, because a is contained in  , as a only occurs once (in the first set).
, as a only occurs once (in the first set).
 (and vice versa).
(and vice versa).
 in the above case). The closure of an LT property P is:
in the above case). The closure of an LT property P is:

 . It does not satisfy the LT property "infinitely often q", because of the path
. It does not satisfy the LT property "infinitely often q", because of the path  . It does satisfy the property "infinitely often p", because all possible paths enter
. It does satisfy the property "infinitely often p", because all possible paths enter  or
or  infinitely often.
infinitely often.
 .
.

 .
.
 i.e. any finite string can be continued to a valid trace. An example of a liveness property is the previous LT property "the set of words that contain a infinitely often". No finite prefix of a word can prove that the word does not satisfy this property, as the word could continue on to have infinitely many as.
i.e. any finite string can be continued to a valid trace. An example of a liveness property is the previous LT property "the set of words that contain a infinitely often". No finite prefix of a word can prove that the word does not satisfy this property, as the word could continue on to have infinitely many as.

