Misplaced Pages

Linear polarization

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Linearly polarized light) Electromagnetic radiation special case

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (May 2020) (Learn how and when to remove this message)
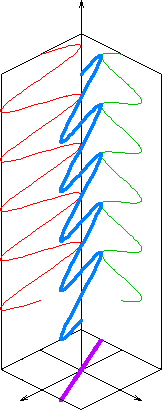
Diagram of the electric field of a light wave (blue), linear-polarized along a plane (purple line), and consisting of two orthogonal, in-phase components (red and green waves)

In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation. The term linear polarization (French: polarisation rectiligne) was coined by Augustin-Jean Fresnel in 1822. See polarization and plane of polarization for more information.

The orientation of a linearly polarized electromagnetic wave is defined by the direction of the electric field vector. For example, if the electric field vector is vertical (alternately up and down as the wave travels) the radiation is said to be vertically polarized.

Mathematical description

The classical sinusoidal plane wave solution of the electromagnetic wave equation for the electric and magnetic fields is (cgs units)

E ( r , t ) = | E | R e { | ψ ⟩ exp ⁡ [ i ( k z − ω t ) ] } {\displaystyle \mathbf {E} (\mathbf {r} ,t)=|\mathbf {E} |\mathrm {Re} \left\{|\psi \rangle \exp \left\right\}}
B ( r , t ) = z ^ × E ( r , t ) / c {\displaystyle \mathbf {B} (\mathbf {r} ,t)={\hat {\mathbf {z} }}\times \mathbf {E} (\mathbf {r} ,t)/c}

for the magnetic field, where k is the wavenumber,

ω = c k {\displaystyle \omega _{}^{}=ck}

is the angular frequency of the wave, and c {\displaystyle c} is the speed of light.

Here ∣ E ∣ {\displaystyle \mid \mathbf {E} \mid } is the amplitude of the field and

| ψ ⟩   = d e f   ( ψ x ψ y ) = ( cos ⁡ θ exp ⁡ ( i α x ) sin ⁡ θ exp ⁡ ( i α y ) ) {\displaystyle |\psi \rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}\psi _{x}\\\psi _{y}\end{pmatrix}}={\begin{pmatrix}\cos \theta \exp \left(i\alpha _{x}\right)\\\sin \theta \exp \left(i\alpha _{y}\right)\end{pmatrix}}}

is the Jones vector in the x-y plane.

The wave is linearly polarized when the phase angles α x , α y {\displaystyle \alpha _{x}^{},\alpha _{y}} are equal,

α x = α y   = d e f   α {\displaystyle \alpha _{x}=\alpha _{y}\ {\stackrel {\mathrm {def} }{=}}\ \alpha } .

This represents a wave polarized at an angle θ {\displaystyle \theta } with respect to the x axis. In that case, the Jones vector can be written

| ψ ⟩ = ( cos ⁡ θ sin ⁡ θ ) exp ⁡ ( i α ) {\displaystyle |\psi \rangle ={\begin{pmatrix}\cos \theta \\\sin \theta \end{pmatrix}}\exp \left(i\alpha \right)} .

The state vectors for linear polarization in x or y are special cases of this state vector.

If unit vectors are defined such that

| x ⟩   = d e f   ( 1 0 ) {\displaystyle |x\rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}1\\0\end{pmatrix}}}

and

| y ⟩   = d e f   ( 0 1 ) {\displaystyle |y\rangle \ {\stackrel {\mathrm {def} }{=}}\ {\begin{pmatrix}0\\1\end{pmatrix}}}

then the polarization state can be written in the "x-y basis" as

| ψ ⟩ = cos ⁡ θ exp ⁡ ( i α ) | x ⟩ + sin ⁡ θ exp ⁡ ( i α ) | y ⟩ = ψ x | x ⟩ + ψ y | y ⟩ {\displaystyle |\psi \rangle =\cos \theta \exp \left(i\alpha \right)|x\rangle +\sin \theta \exp \left(i\alpha \right)|y\rangle =\psi _{x}|x\rangle +\psi _{y}|y\rangle } .

See also

References

  • Jackson, John D. (1998). Classical Electrodynamics (3rd ed.). Wiley. ISBN 0-471-30932-X.
  1. A. Fresnel, "Mémoire sur la double réfraction que les rayons lumineux éprouvent en traversant les aiguilles de cristal de roche suivant les directions parallèles à l'axe", read 9 December 1822; printed in H. de Senarmont, E. Verdet, and L. Fresnel (eds.), Oeuvres complètes d'Augustin Fresnel, vol. 1 (1866), pp. 731–51; translated as "Memoir on the double refraction that light rays undergo in traversing the needles of quartz in the directions parallel to the axis", Zenodo: 4745976, 2021 (open access); §9.
  2. Shapira, Joseph; Shmuel Y. Miller (2007). CDMA radio with repeaters. Springer. p. 73. ISBN 978-0-387-26329-8.

External links

Public Domain This article incorporates public domain material from Federal Standard 1037C. General Services Administration. Archived from the original on January 22, 2022.

Category: