Misplaced Pages

List of shapes with known packing constant

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.

The packing constant of a geometric body is the largest average density achieved by packing arrangements of congruent copies of the body. For most bodies the value of the packing constant is unknown. The following is a list of bodies in Euclidean spaces whose packing constant is known. Fejes Tóth proved that in the plane, a point symmetric body has a packing constant that is equal to its translative packing constant and its lattice packing constant. Therefore, any such body for which the lattice packing constant was previously known, such as any ellipse, consequently has a known packing constant. In addition to these bodies, the packing constants of hyperspheres in 8 and 24 dimensions are almost exactly known.

Image Description Dimension Packing constant Comments
Monohedral prototiles all 1 Shapes such that congruent copies can form a tiling of space
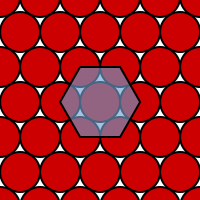Circle, Ellipse 2 π/√12 ≈ 0.906900 Proof attributed to Thue
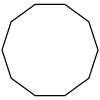
Regular pentagon 2 5 − 5 3 ≈ 0.92131 {\displaystyle {\frac {5-{\sqrt {5}}}{3}}\approx 0.92131} Thomas Hales and Wöden Kusner
Smoothed octagon 2 η s o = 8 − 4 2 − ln ⁡ 2 2 2 − 1 ≈ 0.902414 {\displaystyle \eta _{so}={\frac {8-4{\sqrt {2}}-\ln {2}}{2{\sqrt {2}}-1}}\approx 0.902414} Reinhardt
All 2-fold symmetric convex polygons 2 Linear-time (in number of vertices) algorithm given by Mount and Ruth Silverman
Sphere 3 π/√18 ≈ 0.7404805 See Kepler conjecture
Bi-infinite cylinder 3 π/√12 ≈ 0.906900 Bezdek and Kuperberg
Half-infinite cylinder 3 π/√12 ≈ 0.906900 Wöden Kusner
All shapes contained in a rhombic dodecahedron whose inscribed sphere is contained in the shape 3 Fraction of the volume of the rhombic dodecahedron filled by the shape Corollary of Kepler conjecture. Examples pictured: rhombicuboctahedron and rhombic enneacontahedron.
Hypersphere 8 ( π 2 ) 4 4 ! ≈ 0.2536695 {\displaystyle {\frac {({\frac {\pi }{2}})^{4}}{4!}}\approx 0.2536695} See Hypersphere packing
Hypersphere 24 ( π 2 ) 12 12 ! ≈ 0.000000471087 {\displaystyle {\frac {({\frac {\pi }{2}})^{12}}{12!}}\approx 0.000000471087} See Hypersphere packing

References

  1. ^ Bezdek, András; Kuperberg, Włodzimierz (2010). "Dense packing of space with various convex solids". arXiv:1008.2398v1 .
  2. Fejes Tóth, László (1950). "Some packing and covering theorems". Acta Sci. Math. Szeged. 12.
  3. Cohn, Henry; Kumar, Abhinav (2009). "Optimality and uniqueness of the Leech lattice among lattices". Annals of Mathematics. 170 (3): 1003–1050. arXiv:math/0403263. doi:10.4007/annals.2009.170.1003. S2CID 10696627.
  4. Chang, Hai-Chau; Wang, Lih-Chung (2010). "A Simple Proof of Thue's Theorem on Circle Packing". arXiv:1009.4322v1 .
  5. Hales, Thomas; Kusner, Wöden (2016). "Packings of regular pentagons in the plane". arXiv:1602.07220 .
  6. Reinhardt, Karl (1934). "Über die dichteste gitterförmige Lagerung kongruente Bereiche in der Ebene und eine besondere Art konvexer Kurven". Abh. Math. Sem. Univ. Hamburg. 10: 216–230. doi:10.1007/bf02940676. S2CID 120336230.
  7. Mount, David M.; Silverman, Ruth (1990). "Packing and covering the plane with translates of a convex polygon". Journal of Algorithms. 11 (4): 564–580. doi:10.1016/0196-6774(90)90010-C.
  8. Bezdek, András; Kuperberg, Włodzimierz (1990). "Maximum density space packing with congruent circular cylinders of infinite length". Mathematika. 37: 74–80. doi:10.1112/s0025579300012808.
  9. Kusner, Wöden (2014). "Upper bounds on packing density for circular cylinders with high aspect ratio". Discrete & Computational Geometry. 51 (4): 964–978. arXiv:1309.6996. doi:10.1007/s00454-014-9593-6. S2CID 38234737.
  10. Klarreich, Erica (March 30, 2016), "Sphere Packing Solved in Higher Dimensions", Quanta Magazine
  11. Viazovska, Maryna (2016). "The sphere packing problem in dimension 8". Annals of Mathematics. 185 (3): 991–1015. arXiv:1603.04246. doi:10.4007/annals.2017.185.3.7. S2CID 119286185.
Categories: