Misplaced Pages

Lode coordinates

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Lode angle)

Surfaces on which the invariants ξ {\displaystyle \xi } , ρ {\displaystyle \rho } , θ {\displaystyle \theta } are constant. Plotted in principal stress space. The red plane represents a meridional plane and the yellow plane an octahedral plane.

Lode coordinates ( z , r , θ ) {\displaystyle (z,r,\theta )} or Haigh–Westergaard coordinates ( ξ , ρ , θ ) {\displaystyle (\xi ,\rho ,\theta )} . are a set of tensor invariants that span the space of real, symmetric, second-order, 3-dimensional tensors and are isomorphic with respect to principal stress space. This right-handed orthogonal coordinate system is named in honor of the German scientist Dr. Walter Lode because of his seminal paper written in 1926 describing the effect of the middle principal stress on metal plasticity. Other examples of sets of tensor invariants are the set of principal stresses ( σ 1 , σ 2 , σ 3 ) {\displaystyle (\sigma _{1},\sigma _{2},\sigma _{3})} or the set of kinematic invariants ( I 1 , J 2 , J 3 ) {\displaystyle (I_{1},J_{2},J_{3})} . The Lode coordinate system can be described as a cylindrical coordinate system within principal stress space with a coincident origin and the z-axis parallel to the vector ( σ 1 , σ 2 , σ 3 ) = ( 1 , 1 , 1 ) {\displaystyle (\sigma _{1},\sigma _{2},\sigma _{3})=(1,1,1)} .

Mechanics invariants

The Lode coordinates are most easily computed using the mechanics invariants. These invariants are a mixture of the invariants of the Cauchy stress tensor, σ {\displaystyle {\boldsymbol {\sigma }}} , and the stress deviator, s {\displaystyle {\boldsymbol {s}}} , and are given by

I 1 = t r ( σ ) {\displaystyle I_{1}=\mathrm {tr} ({\boldsymbol {\sigma }})}
J 2 = 1 2 [ tr ( σ 2 ) − 1 3 tr ( σ ) 2 ] = 1 2 t r ( s ⋅ s ) = 1 2 ‖ s ‖ 2 {\displaystyle J_{2}={\frac {1}{2}}\left={\frac {1}{2}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)={\frac {1}{2}}\lVert {\boldsymbol {s}}\rVert ^{2}}
J 3 = d e t ( s ) = 1 3 t r ( s ⋅ s ⋅ s ) {\displaystyle J_{3}=\mathrm {det} ({\boldsymbol {s}})={\frac {1}{3}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)}

which can be written equivalently in Einstein notation

I 1 = σ k k {\displaystyle I_{1}=\sigma _{kk}}
J 2 = 1 2 [ tr ( σ 2 ) − 1 3 tr ( σ ) 2 ] = 1 2 s i j s j i = 1 2 s i j s i j {\displaystyle J_{2}={\frac {1}{2}}\left={\frac {1}{2}}s_{ij}s_{ji}={\frac {1}{2}}s_{ij}s_{ij}}
J 3 = 1 6 ϵ i j k ϵ p q r σ i p σ j q σ k r = 1 3 s i j s j k s k i {\displaystyle J_{3}={\frac {1}{6}}\epsilon _{ijk}\epsilon _{pqr}\sigma _{ip}\sigma _{jq}\sigma _{kr}={\frac {1}{3}}s_{ij}s_{jk}s_{ki}}

where ϵ {\displaystyle \epsilon } is the Levi-Civita symbol (or permutation symbol) and the last two forms for J 2 {\displaystyle J_{2}} are equivalent because s {\displaystyle {\boldsymbol {s}}} is symmetric ( s i j = s j i {\displaystyle s_{ij}=s_{ji}} ).

The gradients of these invariants can be calculated by

∂ I 1 ∂ σ = I {\displaystyle {\frac {\partial I_{1}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {I}}}
∂ J 2 ∂ σ = s = σ − t r ( σ ) 3 I {\displaystyle {\frac {\partial J_{2}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {s}}={\boldsymbol {\sigma }}-{\frac {\mathrm {tr} \left({\boldsymbol {\sigma }}\right)}{3}}{\boldsymbol {I}}}
∂ J 3 ∂ σ = T = s ⋅ s − 2 J 2 3 I {\displaystyle {\frac {\partial J_{3}}{\partial {\boldsymbol {\sigma }}}}={\boldsymbol {T}}={\boldsymbol {s}}\cdot {\boldsymbol {s}}-{\frac {2J_{2}}{3}}{\boldsymbol {I}}}

where I {\displaystyle {\boldsymbol {I}}} is the second-order identity tensor and T {\displaystyle {\boldsymbol {T}}} is called the Hill tensor.

Axial coordinate ( z ) {\displaystyle (z)}

The z {\displaystyle z} -coordinate is found by calculating the magnitude of the orthogonal projection of the stress state onto the hydrostatic axis.

z = E z : σ = t r ( σ ) 3 = I 1 3 {\displaystyle z={\boldsymbol {E_{z}}}\colon {\boldsymbol {\sigma }}={\frac {\mathrm {tr} ({\boldsymbol {\sigma }})}{\sqrt {3}}}={\frac {I_{1}}{\sqrt {3}}}}

where

E z = I ‖ I ‖ = I 3 {\displaystyle {\boldsymbol {E_{z}}}={\frac {\boldsymbol {I}}{\lVert {\boldsymbol {I}}\rVert }}={\frac {\boldsymbol {I}}{\sqrt {3}}}}

is the unit normal in the direction of the hydrostatic axis.

Radial coordinate ( r ) {\displaystyle (r)}

The r {\displaystyle r} -coordinate is found by calculating the magnitude of the stress deviator (the orthogonal projection of the stress state into the deviatoric plane).

r = E r : σ = ‖ s ‖ = 2 J 2 {\displaystyle r={\boldsymbol {E_{r}}}\colon {\boldsymbol {\sigma }}=\lVert {\boldsymbol {s}}\rVert ={\sqrt {2J_{2}}}}

where

E r = s ‖ s ‖ {\displaystyle {\boldsymbol {E_{r}}}={\frac {\boldsymbol {s}}{\lVert {\boldsymbol {s}}\rVert }}}
Derivation
The relation that r = 2 J 2 {\displaystyle r={\sqrt {2J_{2}}}} can be found by expanding the relation
r = s ‖ s ‖ : σ {\displaystyle r={\frac {\boldsymbol {s}}{\lVert {\boldsymbol {s}}\rVert }}\colon {\boldsymbol {\sigma }}}

and writing σ {\displaystyle \sigma } in terms of the isotropic and deviatoric parts while expanding the magnitude of s {\displaystyle {\boldsymbol {s}}}

r = s s : s : ( s + z E z ) = 1 s : s ( s : s + z s : E z ) {\displaystyle r={\frac {\boldsymbol {s}}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}\colon \left({\boldsymbol {s}}+z{\boldsymbol {E_{z}}}\right)={\frac {1}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}\left({\boldsymbol {s}}\colon {\boldsymbol {s}}+z{\boldsymbol {s}}\colon {\boldsymbol {E_{z}}}\right)} .

Because E z {\displaystyle {\boldsymbol {E_{z}}}} is isotropic and s {\displaystyle {\boldsymbol {s}}} is deviatoric, their product is zero. Which leaves us with

r = s : s s : s = s : s {\displaystyle r={\frac {{\boldsymbol {s}}\colon {\boldsymbol {s}}}{\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}={\sqrt {{\boldsymbol {s}}\colon {\boldsymbol {s}}}}}

Applying the identity A : B = t r ( A T ⋅ B ) {\displaystyle {\boldsymbol {A}}\colon {\boldsymbol {B}}=\mathrm {tr} \left({\boldsymbol {A}}^{T}\cdot {\boldsymbol {B}}\right)} and using the definition of J 2 = 1 2 t r ( s ⋅ s ) {\displaystyle J_{2}={\frac {1}{2}}\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)}

r = t r ( s ⋅ s ) = 2 J 2 {\displaystyle r={\sqrt {\mathrm {tr} \left({\boldsymbol {s}}\cdot {\boldsymbol {s}}\right)}}={\sqrt {2J_{2}}}}

is a unit tensor in the direction of the radial component.

Lode angle – angular coordinate ( θ ) {\displaystyle (\theta )}

This plot demonstrates that an intuitive approximation for the Lode angle is the relative position of the middle principal stress λ m {\displaystyle \lambda _{m}} with respect to the low and high principal stresses.

The Lode angle can be considered, rather loosely, a measure of loading type. The Lode angle varies with respect to the middle eigenvalue of the stress. There are many definitions of Lode angle that each utilize different trigonometric functions: the positive sine, negative sine, and positive cosine (here denoted θ s {\displaystyle \theta _{s}} , θ ¯ s {\displaystyle {\bar {\theta }}_{s}} , and θ c {\displaystyle \theta _{c}} , respectively)

sin ⁡ ( 3 θ s ) = − sin ⁡ ( 3 θ ¯ s ) = cos ⁡ ( 3 θ c ) = J 3 2 ( 3 J 2 ) 3 / 2 {\displaystyle \sin(3\theta _{s})=-\sin(3{\bar {\theta }}_{s})=\cos(3\theta _{c})={\frac {J_{3}}{2}}\left({\frac {3}{J_{2}}}\right)^{3/2}}

and are related by

θ s = π 6 − θ c θ s = − θ ¯ s {\displaystyle \theta _{s}={\frac {\pi }{6}}-\theta _{c}\qquad \qquad \theta _{s}=-{\bar {\theta }}_{s}}
Derivation
The relation between θ c {\displaystyle \theta _{c}} and θ s {\displaystyle \theta _{s}} can be shown by applying a trigonometric identity relating sine and cosine by a shift
cos ⁡ ( 3 θ c ) = sin ⁡ ( 3 θ s ) {\displaystyle \cos(3\theta _{c})=\sin(3\theta _{s})}
cos ⁡ ( 3 θ c ) = sin ⁡ ( ( 3 θ s − π 2 ) + π 2 ) {\displaystyle \cos(3\theta _{c})=\sin \left(\left(3\theta _{s}-{\frac {\pi }{2}}\right)+{\frac {\pi }{2}}\right)}
cos ⁡ ( 3 θ c ) = cos ⁡ ( 3 θ s − π 2 ) {\displaystyle \cos(3\theta _{c})=\cos \left(3\theta _{s}-{\frac {\pi }{2}}\right)} .

Because cosine is an even function and the range of the inverse cosine is usually 0 ≤ cos − 1 ⁡ ( θ ) ≤ 1 {\displaystyle 0\leq \cos ^{-1}(\theta )\leq 1} we take the negative possible value for the θ s {\displaystyle \theta _{s}} term, thus ensuring that θ c {\displaystyle \theta _{c}} is positive.

3 θ c = ± ( 3 θ s − π 2 ) {\displaystyle 3\theta _{c}=\pm \left(3\theta _{s}-{\frac {\pi }{2}}\right)}
θ c = π 6 − θ s {\displaystyle \theta _{c}={\frac {\pi }{6}}-\theta _{s}}

These definitions are all defined for a range of π / 3 {\displaystyle \pi /3} .

Stress State σ 1 ≥ σ 2 ≥ σ 3 {\displaystyle \sigma _{1}\geq \sigma _{2}\geq \sigma _{3}} θ s {\displaystyle \theta _{s}} θ ¯ s {\displaystyle {\bar {\theta }}_{s}} θ c {\displaystyle \theta _{c}}
range − π 6 ≤ θ s ≤ π 6 {\displaystyle -{\frac {\pi }{6}}\leq \theta _{s}\leq {\frac {\pi }{6}}} − π 6 ≤ θ s ≤ π 6 {\displaystyle -{\frac {\pi }{6}}\leq \theta _{s}\leq {\frac {\pi }{6}}} 0 ≤ θ c ≤ π 3 {\displaystyle 0\leq \theta _{c}\leq {\frac {\pi }{3}}}
Triaxial Compression (TXC) σ 1 ≥ σ 2 = σ 3 {\displaystyle \sigma _{1}\geq \sigma _{2}=\sigma _{3}} − π 6 {\displaystyle -{\frac {\pi }{6}}} π 6 {\displaystyle {\frac {\pi }{6}}} π 3 {\displaystyle {\frac {\pi }{3}}}
Shear (SHR) σ 2 = ( σ 1 + σ 3 ) / 2 {\displaystyle \sigma _{2}=(\sigma _{1}+\sigma _{3})/2} 0 {\displaystyle 0} 0 {\displaystyle 0} π 6 {\displaystyle {\frac {\pi }{6}}}
Triaxial Extension (TXE) σ 1 = σ 2 ≥ σ 3 {\displaystyle \sigma _{1}=\sigma _{2}\geq \sigma _{3}} π 6 {\displaystyle {\frac {\pi }{6}}} − π 6 {\displaystyle -{\frac {\pi }{6}}} 0 {\displaystyle 0}

The unit normal in the angular direction which completes the orthonormal basis can be calculated for θ s {\displaystyle \theta _{s}} and θ c {\displaystyle \theta _{c}} using

E θ s = T / ‖ T ‖ − sin ⁡ ( 3 θ s ) E r cos ⁡ ( 3 θ s ) E θ c = T / ‖ T ‖ − cos ⁡ ( 3 θ c ) E r sin ⁡ ( 3 θ c ) {\displaystyle {\boldsymbol {E_{\theta s}}}={\frac {{\boldsymbol {T}}/\lVert {\boldsymbol {T}}\rVert -\sin(3\theta _{s}){\boldsymbol {E_{r}}}}{\cos(3\theta _{s})}}\qquad {\boldsymbol {E_{\theta c}}}={\frac {{\boldsymbol {T}}/\lVert {\boldsymbol {T}}\rVert -\cos(3\theta _{c}){\boldsymbol {E_{r}}}}{\sin(3\theta _{c})}}} .

Meridional profile

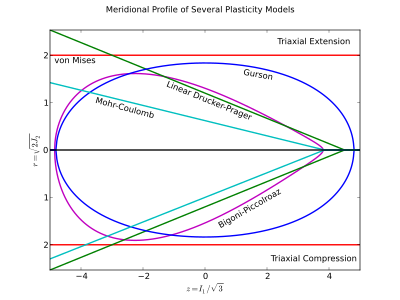
This plot shows a typical meridional profile of several plasticity models: von Mises, linear Drucker–Prager, Mohr–Coulomb, Gurson, and Bigoni–Piccolroaz. The upper portion of the plot depicts yield surface behavior in triaxial extension and the lower portion depicts yield surface behavior in triaxial compression.

The meridional profile is a 2D plot of ( z , r ) {\displaystyle (z,r)} holding θ {\displaystyle \theta } constant and is sometimes plotted using scalar multiples of ( z , r ) {\displaystyle (z,r)} . It is commonly used to demonstrate the pressure dependence of a yield surface or the pressure-shear trajectory of a stress path. Because r {\displaystyle r} is non-negative the plot usually omits the negative portion of the r {\displaystyle r} -axis, but can be included to illustrate effects at opposing Lode angles (usually triaxial extension and triaxial compression).

One of the benefits of plotting the meridional profile with ( z , r ) {\displaystyle (z,r)} is that it is a geometrically accurate depiction of the yield surface. If a non-isomorphic pair is used for the meridional profile then the normal to the yield surface will not appear normal in the meridional profile. Any pair of coordinates that differ from ( z , r ) {\displaystyle (z,r)} by constant multiples of equal absolute value are also isomorphic with respect to principal stress space. As an example, pressure p = − I 1 / 3 {\displaystyle p=-I1/3} and the Von Mises stress σ v = 3 J 2 {\displaystyle \sigma _{v}={\sqrt {3J_{2}}}} are not an isomorphic coordinate pair and, therefore, distort the yield surface because

p = − 1 3 z {\displaystyle p=-{\frac {1}{\sqrt {3}}}z}
σ v = 3 2 r {\displaystyle \sigma _{v}={\sqrt {\frac {3}{2}}}r}

and, finally, | − 1 / 3 | ≠ | 3 / 2 | {\displaystyle |-1/{\sqrt {3}}|\neq |{\sqrt {3/2}}|} .

Octahedral profile

This plot shows a typical octahedral profile of several plasticity models: von Mises, linear Drucker–Prager, Mohr–Coulomb, Gurson, and Bigoni–Piccolroaz. This plot has omitted Lode angle values in favor of loading descriptions because of the preponderance of definitions of the Lode angle. The radial coordinate is r = 2 J 2 {\displaystyle r={\sqrt {2J_{2}}}} .

The octahedral profile is a 2D plot of ( r , θ ) {\displaystyle (r,\theta )} holding z {\displaystyle z} constant. Plotting the yield surface in the octahedral plane demonstrates the level of Lode angle dependence. The octahedral plane is sometimes referred to as the 'pi plane' or 'deviatoric plane'.

The octahedral profile is not necessarily constant for different values of pressure with the notable exceptions of the von Mises yield criterion and the Tresca yield criterion which are constant for all values of pressure.

A note on terminology

The term Haigh-Westergaard space is ambiguously used in the literature to mean both the Cartesian principal stress space and the cylindrical Lode coordinate space

See also

References

  1. Menetrey, Philippe; Willam, K. J.; 1995, "Triaxial Failure Criterion for Concrete and its Generalization", Structural Journal, American Concrete Institute, Volume 92, Issue 3, pages 311-318, DOI: 10.14359/1132
  2. Lode, Walter (1926), „Versuche über den Einfluß der mittleren Hauptspannung auf das Fließen der Metalle Eisen, Kupfer und Nickel“ , Zeitschrift für Physik, vol. 36 (November), pp. 913–939, DOI: 10.1007/BF01400222
  3. Asaro, Robert J.; Lubarda, Vlado A.; 2006, Mechanics of Solids and Materials, Cambridge University Press
  4. Brannon, Rebecca M.; 2009, KAYENTA: Theory and User's Guide, Sandia National Laboratories, Albuquerque, New Mexico.
  5. Chakrabarty, Jagabanduhu; 2006, Theory of Plasticity: Third edition, Elsevier, Amsterdam.
  6. de Souza Neto, Eduardo A.; Peric, Djordje; Owen, David R. J.; 2008, Computational Methods for Plasticity: Theory and Applications, Wiley
  7. Han, D. J.; Chen, Wai-Fah; 1985, "A Nonuniform Hardening Plasticity Model for Concrete Materials", Mechanics of Materials, Volume 4, Issues 3–4, December 1985, Pages 283-302, doi: 10.1016/0167-6636(85)90025-0
  8. ^ Brannon, Rebecca M.; 2007, Elements of Phenomenological Plasticity: Geometrical Insight, Computational Algorithms, and Topics in Shock Physics, Shock Wave Science and Technology Reference Library: Solids I, Springer-New York
  9. Bigoni, Davide; Piccolroaz, Andrea; 2004, "Yield criteria for quasibrittle and frictional materials", International Journal of Solids and Structures, Volume 41, Issues 11–12, June 2004, Pages 2855-2878, doi: 10.1016/j.ijsolstr.2003.12.024
  10. Lubliner, Jacob; 1990, Plasticity Theory, Pearson Education
  11. Chaboche, J.-L.; 2008, "A review of some plasticity and viscoplasticity theories", International Journal of Plasticity, 24(10):1642-1693, DOI:10.1016/j.ijplas.2008.03.009
  12. Mouazen, Abdul Mounem; Neményi, Miklós; 1998, "A review of the finite element modelling techniques of soil tillage", Mathematics and Computers in Simulation, Volume 48, Issue 1, 1 November 1998, Pages 23-32, doi: 10.1016/S0378-4754(98)00152-9
  13. Keryvin, Vincent; 2008, "Indentation as a probe for pressure sensitivity of metallic glasses", Journal of Physics: Condensed Matter, Volume 20, Number 11, DOI: 10.1088/0953-8984/20/11/114119
  14. Červenka, Jan; Papanikolaou, Vassilis K.; 2008, "Three dimensional combined fracture–plastic material model for concrete", International Journal of Plasticity, Volume 24, Issue 12, December 2008, Pages 2192-2220, doi: 10.1016/j.ijplas.2008.01.004
  15. Piccolroaz, Andrea; Bigoni, Davide; 2009, "Yield criteria for quasibrittle and frictional materials: A generalization to surfaces with corners", International Journal of Solids and Structures, Volume 46, Issue 20, 1 October 2009, Pages 3587-3596, doi: 10.1016/j.ijsolstr.2009.06.006
Categories: