Misplaced Pages

MacMahon Squares

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Puzzle published in 1921 by Percy MacMahon
This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.
Find sources: "MacMahon Squares" – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this message)
MacMahon Squares
A particular solution; this illustrates the B20,0,0 constraint which forces a single color along the perimeter, while also maximizing the largest contiguous single-color area within the perimeter

MacMahon Squares are an edge-matching puzzle first published by Percy MacMahon in 1921, using 24 unique squares with 3-color patterns; each of the four edges is assigned a single color. The complete set of 24 squares are organized next to each other by matching edge colors to create a 4 by 6 grid. Such tessellation puzzles have multiple variants, which are determined by restrictions on how to arrange the 24 squares. This game has also been commercialized in numerous physical forms, by various companies.

The game

MacMahon Squares
All 24 MacMahon Squares, redrawn from Fig. 26 of New Mathematical Pastimes (MacMahon, 1921)

MacMahon squares was first published in Percy Alexander MacMahon's 1921 treatise New Mathematical Pastimes. The original version consisted of one copy of each of the 24 different squares that can be made by coloring the edges of a square with one of three colors. (Here "different" means up to rotations.) The goal is to arrange the squares into a 4 by 6 grid so that when two squares share an edge, the common edge is the same color in both squares.

In 1964, a supercomputer was used to produce 12,261 solutions to the basic version of the MacMahon Squares puzzle, with a runtime of about 40 hours.

MacMahon squares (3 colors)
Single color Two colors Three colors
Quads Triples Doubles Doubles
   
1111 1112 1113 1122 1133 1123 1132 1213
   
2222 1222 2223 1212 2233 1223 1322 1232
   
3333 1333 2333 1313 2323 1233 1332 1323

Theory

The MacMahon Squares game is an example of an edge-matching puzzle. The family of such problems is NP-complete. The first part of New Mathematical Diversions describes these games in general, starting with linear forms (dominoes), then progressing in detail with similar games using tiles shaped as equilateral triangles, squares, right isoceles triangles, cubes, and hexagons.

There are a total of 24 distinct squares for 3 colors. For an arbitrary number of colors n {\displaystyle n} , the number of unique squares can be found by the expression n 4 ⋅ ( n + 1 ) ⋅ ( n 2 − n + 2 ) {\displaystyle {\frac {n}{4}}\cdot (n+1)\cdot (n^{2}-n+2)} .

For other shapes with n {\displaystyle n} colors, MacMahon determined the number of unique patterns are:

  • Triangle: n 3 ⋅ ( n 2 + 2 ) {\displaystyle {\frac {n}{3}}\cdot (n^{2}+2)}
  • Pentagon: n 5 ⋅ ( n 4 + 4 ) {\displaystyle {\frac {n}{5}}\cdot (n^{4}+4)}
  • Hexagon: n 6 ⋅ ( n + 1 ) ⋅ ( n 4 − n 3 + n 2 + 2 ) {\displaystyle {\frac {n}{6}}\cdot (n+1)\cdot (n^{4}-n^{3}+n^{2}+2)}
  • Heptagon: n 7 ⋅ ( n 6 + 6 ) {\displaystyle {\frac {n}{7}}\cdot (n^{6}+6)}

For example, given a triangle with three sides, each of which is assigned one of four possible colors, there are 56 unique patterns.

Variants

  • MacMahon Squares sample solutions
  • C1,1,1 B10,10,0 (Fig. 27) C1,1,1 B10,10,0 (Fig. 27)
  • C1,2 B20,0,0 (Fig. 28) C1,2 B20,0,0 (Fig. 28)
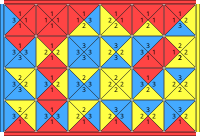  • C1,2 B12,4,4 (Fig. 28) C1,2 B12,4,4 (Fig. 28)

Contact system

In his book, MacMahon suggested the ability to define which borders can contact one another, based on their colors. This is by some permutation of the 3 colors, described by Ca,b,c. Here, a, b, and c represent the shift in colors to which the first, second, and third colors can be matched to. A '1' it is matched to itself, and a '2' signifies that it must be matched with a different color.

For example, C1,1,1 represents 1 to 1, 2 to 2, and 3 to 3, as each of these matchings are represented by the number 1. Alternatively, C1,2 represents 1 to 1 and 2 to 3 as the 1 to 1 matching is represented by the number 1, and the matching between 2 and 3 is represented by 2. More colors can be described in a similar way. For example, a coloring of C1,2,2,2 represents 1 to 1, 2 to 3, 4 to 5, and 6 to 7.

From here we can see that the only possible numbers to describe the pairings by are 1 and 2, since a 3 or above merely skips over a color that would be used the same otherwise because colorings are relative.

Boundaries

Another way to change the puzzle is to restrict which colors squared make up the border colors. In the classic MacMahon squares puzzle, there are a total of 20 places on the border. The number of each color that can be present on these 20 places can be described by Ba,b,c where a, b, and c are the number of each color of the border pieces.

For example, B20,0,0 represents 20 of the first color and none of the rest since the first color already constitutes all available border spaces. Alternatively, B10,10,0 represents 10 of the first color and 10 of the next. More colors can be described in a similar way. For example, a boundary of B22,16,8,2 represents 22 of the first, 16 of the second, 8 of the next, and 2 of the last colors to populate the border colors.

From here we can see that the only possible numbers to describe the number of each color composing the boundary are even numbers, since this would imply an odd number of another color, which would violate the parity of the total number of triangles.

Analogous puzzles

MacMahon Squares, along with variations on the idea, was commercialized as Multimatch.

Another puzzle with similar properties is MacMahon's Cubes, which are a set of 30 cubes, with sides colored one of 6 different colors. Unlike the MacMahon Squares puzzle, we do not include all 2,226 possible cubes, but only the cubes containing exactly 6 distinct colors and 1 of each of the 6 colors.

MacMahon Squares have served as a baseline for numerous other puzzles. Some of these include the Nelson Puzzle, the Wang Tile, and TetraVex.

The commercial board game Trioker, patented in 1969 by Marc Odier, uses triangular tiles first proposed by MacMahon in 1921.

Notes

  1. The nomenclature in this table is intended to be orientation-agnostic, starting from the edge(s) with the lowest value and proceeding anti-clockwise. For example, the tile 1232 has the lowest color value 1, followed sequentially by 2 (immediately anti-clockwise of color value 1), then 3, and finally 2 again.
  2. With three colors and four edges, one color will be repeated at least once.

References

  1. ^ MacMahon, P. A. (1921). New Mathematical Pastimes. Cambridge University Press. Retrieved 19 December 2023.
  2. "MacMahon 3-Color Squares". Retrieved 2021-04-06.
  3. ^ Gardner, Martin. "The 24 Color Squares and the 30 Color Cubes". New Mathematical Diversions (PDF). p. 184.
  4. "Age of Puzzles - Harry L. Nelson". www.ageofpuzzles.com. Retrieved 2021-04-06.

External links

  1. MacMahon Squares Online
Category: