Misplaced Pages

Mac Lane coherence theorem

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Mac Lane's coherence theorem)

In category theory, a branch of mathematics, Mac Lane's coherence theorem states, in the words of Saunders Mac Lane, “every diagram commutes”. But regarding a result about certain commutative diagrams, Kelly is states as follows: "no longer be seen as constituting the essence of a coherence theorem". More precisely (cf. #Counter-example), it states every formal diagram commutes, where "formal diagram" is an analog of well-formed formulae and terms in proof theory.

The theorem can be stated as a strictification result; namely, every monoidal category is monoidally equivalent to a strict monoidal category.

Counter-example

It is not reasonable to expect we can show literally every diagram commutes, due to the following example of Isbell.

Let S e t 0 ⊂ S e t {\displaystyle {\mathsf {Set}}_{0}\subset {\mathsf {Set}}} be a skeleton of the category of sets and D a unique countable set in it; note D × D = D {\displaystyle D\times D=D} by uniqueness. Let p : D = D × D → D {\displaystyle p:D=D\times D\to D} be the projection onto the first factor. For any functions f , g : D → D {\displaystyle f,g:D\to D} , we have f ∘ p = p ∘ ( f × g ) {\displaystyle f\circ p=p\circ (f\times g)} . Now, suppose the natural isomorphisms α : X × ( Y × Z ) ≃ ( X × Y ) × Z {\displaystyle \alpha :X\times (Y\times Z)\simeq (X\times Y)\times Z} are the identity; in particular, that is the case for X = Y = Z = D {\displaystyle X=Y=Z=D} . Then for any f , g , h : D → D {\displaystyle f,g,h:D\to D} , since α {\displaystyle \alpha } is the identity and is natural,

f ∘ p = p ∘ ( f × ( g × h ) ) = p ∘ α ∘ ( f × ( g × h ) ) = p ∘ ( ( f × g ) × h ) ∘ α = ( f × g ) ∘ p {\displaystyle f\circ p=p\circ (f\times (g\times h))=p\circ \alpha \circ (f\times (g\times h))=p\circ ((f\times g)\times h)\circ \alpha =(f\times g)\circ p} .

Since p {\displaystyle p} is an epimorphism, this implies f = f × g {\displaystyle f=f\times g} . Similarly, using the projection onto the second factor, we get g = f × g {\displaystyle g=f\times g} and so f = g {\displaystyle f=g} , which is absurd.

Proof

This section needs expansion. You can help by adding to it. (February 2022)

Coherence condition (Monoidal category)

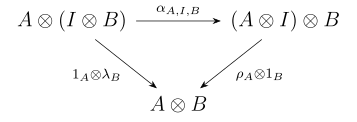
In monoidal category C {\displaystyle C} , the following two conditions are called coherence conditions:

  • Let a bifunctor ⊗ : C × C → C {\displaystyle \otimes \colon \mathbf {C} \times \mathbf {C} \to \mathbf {C} } called the tensor product, a natural isomorphism α A , B , C {\displaystyle \alpha _{A,B,C}} , called the associator:
α A , B , C : ( A ⊗ B ) ⊗ C → A ⊗ ( B ⊗ C ) {\displaystyle \alpha _{A,B,C}\colon (A\otimes B)\otimes C\rightarrow A\otimes (B\otimes C)}
  • Also, let I {\displaystyle I} an identity object and I {\displaystyle I} has a left identity, a natural isomorphism λ A {\displaystyle \lambda _{A}} called the left unitor:
λ A : I ⊗ A → A {\displaystyle \lambda _{A}:I\otimes A\rightarrow A}
as well as, let I {\displaystyle I} has a right identity, a natural isomorphism ρ A {\displaystyle \rho _{A}} called the right unitor:
ρ A : A ⊗ I → A {\displaystyle \rho _{A}:A\otimes I\rightarrow A} .

Pentagon and triangle identity

To satisfy the coherence condition, it is enough to prove just the pentagon and triangle identity, which is essentially the same as what is stated in Kelly's (1964) paper.

See also

Notes

  1. Mac Lane 1998, Ch VII, § 2.
  2. Kelly 1974, 1.2
  3. Schauenburg 2001
  4. Mac Lane 1998, Ch VII. the end of § 1.
  5. Kelly 1964

References

Further reading

External links

Stub icon

This category theory-related article is a stub. You can help Misplaced Pages by expanding it.

Categories: