Misplaced Pages

Part of a series on
Antennas
Common types Dipole Fractal Loop Monopole Satellite dish Television Whip
Components Balun Block upconverter Coaxial cable Counterpoise (ground system) Feed Feed line Low-noise block downconverter Passive radiator Receiver Rotator Stub Transmitter Tuner Twin-lead
Systems Antenna farm Amateur radio Cellular network Hotspot Municipal wireless network Radio Radio masts and towers Wi-Fi Wireless
Safety and regulation Wireless device radiation and health Wireless electronic devices and health International Telecommunication Union (Radio Regulations) World Radiocommunication Conference
Radiation sources / regions Boresight Focal cloud Ground plane Main lobe Near and far field Side lobe Vertical plane
Characteristics Array gain Directivity Efficiency Electrical length Equivalent radius Factor Friis transmission equation Gain Height Radiation pattern Radiation resistance Radio propagation Radio spectrum Signal-to-noise ratio Spurious emission
Techniques Beam steering Beam tilt Beamforming Small cell Bell Laboratories Layered Space-Time (BLAST) Massive Multiple-input multiple-output (MIMO) Reconfiguration Spread spectrum Wideband Space Division Multiple Access (WSDMA)
v t e

A loop antenna is a radio antenna consisting of a loop or coil of wire, tubing, or other electrical conductor, that for transmitting is usually fed by a balanced power source or for receiving feeds a balanced load. Within this physical description there are two (possibly three) distinct types:

Large loop antennas

Large loops are also called self-resonant loop antennas or full-wave loops; they have a perimeter close to one or more whole wavelengths at the operating frequency, which makes them self-resonant at that frequency. They are the most efficient of all antenna types for both transmission and reception. Large loop antennas have a two-lobe radiation pattern at their first, full-wave resonance, peaking in both directions perpendicular to the plane of the loop Large loops are the most efficient, by an order of magnitude, of all antenna designs of similar size.

Halo antennas

Halos are often explained as shortened dipoles that have been bent into a circular loop, with the ends not quite touching. Some writers prefer to exclude them from loop antennas, since they can be well-understood as bent dipoles, others make halos an intermediate category between large and small loops, or the extreme upper size limit for small transmitting loops: In shape and performance halo antennas are very similar to small loops, only distinguished by being self resonant and having much higher radiation resistance. (See discussion below)

Small loop antennas

Small loops are also called magnetic loops or tuned loops; they have a perimeter smaller than half the operating wavelength (typically no more than ⁠ 1 /3⁠~⁠ 1 /4⁠ wave). They are used mainly as receiving antennas, but are sometimes used for transmission despite their reduced efficiency; loops with a circumference smaller than about ⁠1/ 10 ⁠ wavelength become so inefficient they are rarely used for transmission. A common example of small loop is the ferrite (loopstick) antenna used in most AM broadcast radios. The radiation pattern of small loop antennas is maximum at directions within the plane of the loop, so perpendicular to the maxima of large loops.

Small loops divide into two sub-types, depending on the purpose they are optimized for:

Receiving

Small receiving loops are compact antennas optimized to capture radio waves much longer than their size, where full-sized antennas would be either infeasible or impossible. If their perimeters are kept shorter than ⁠1/ 10 ⁠ wave, they have exceptionally precise "null" directions (where the signal vanishes) which gives a tiny antenna for exceedingly accurate direction-finding, better than most moderately large antennas, and as good as many huge antennas.

Transmitting

Small transmitting loops are optimized for compact antennas that are the "least-worst" signal radiators. Small antennas of any kind are inefficient, but when a full-sized antenna is not practical, making a small loop with a perimeter as close to ⁠1/ 2 ⁠ wave as possible (although usually no more than 0.3 wave) makes the small loop better for transmitting, although it sacrifices or outright loses the precise "null" direction of smaller small loops.

Large, self-resonant loop antennas

For the description of large loops in this section, the radio's operating frequency is assumed to be tuned to the loop antenna's first resonance. At that frequency, one whole free-space wavelength is slightly smaller than the perimeter of the loop, which is the smallest that a "large" loop can be.

Self-resonant loop antennas for so-called “short” wave frequencies are relatively large, with a perimeter just greater than the intended wavelength of operation, hence for circular loops diameters between roughly 175 ft (53 m) at the largest, around 1.8 MHz. At higher frequencies their sizes become smaller, falling to a diameter of about 11 ft (3.4 m) at 30 MHz.

Large loop antennas can be thought of as a folded dipole whose parallel wires have been split apart and opened out into some oval or polygonal shape. The loop's shape can be a circle, triangle, square, rectangle, or in fact any closed polygon, but for resonance the loop perimeter must be slightly larger than a wavelength.

Shape

Loop antennas may be in the shape of a circle, a square or any other closed geometric shape that allows the total perimeter to be slightly more than one wavelength. The most popular shape in amateur radio is the quad antenna or "quad", a self-resonant loop in a square shape so that it can be constructed of wire strung across a supporting ‘×’ shaped frame. There may be one or more additional loops stacked parallel to the first as 'parasitic' director and / or reflector element(s), creating an antenna array which is unidirectional with gain that increases with each additional parasitic element. This design can also be turned 45 degrees to a diamond shape supported on a ‘+’ shaped frame. Triangular loops (‘△’) have also been used for vertical loops, since they can be supported from a single mast. A rectangle twice as high as its width obtains slightly increased gain and also matches 50 Ω directly if used as a single element.

Unlike a dipole antenna, the polarization of a resonant loop antenna is not obvious from the orientation of the loop itself, but depends on the placement of its feedpoint. If a vertically oriented loop is fed at the bottom, its radiation will be horizontally polarized; feeding it from the side will make it vertically polarized.

Radiation pattern

The radiation pattern of a first-resonance loop antenna peaks at right angles to the plane of the loop. As the frequency progresses to the second and third resonances the perpendicular radiation fades and strong lobes near the plane of the loop arise.

At the lower shortwave frequencies a full loop is physically quite large, and its only practical installation is "lying flat", with the plane of the loop horizontal to the ground and the antenna wire supported at the same relatively low height by masts along its perimeter. This results in horizontally-polarized radiation, which peaks toward the vertical near the lowest harmonic; that pattern is good for regional NVIS communication, but unfortunately is not generally useful for making continental-scale contacts.

Above about 10 MHz the loop is approximately 10 meters in diameter, and it becomes more practical for the loop to be mounted "standing up" – that is with the plane of the loop vertical, in order to direct its main beam towards the horizon. If the frequency is high enough, the loop might be small enough to attach to an antenna rotator, in order to rotate that direction as desired. Compared to a dipole or folded dipole, a vertical large loop wastes less power radiating toward the sky or ground, resulting in about 1.5 dB higher gain in the two favored horizontal directions.

Additional gain (and a uni-directional radiation pattern) is usually obtained with an array of such elements either as a driven endfire array or in a Yagi configuration – with only one of the loops being driven by the feedline and all the remaining loops being "parasitic" reflectors and directors. The latter is widely used in amateur radio in the "quad" configuration (see photo).

Low frequency one wavelength loops "lying down" are sometimes used for local NVIS communication. This is sometimes called a lazy quad. Its radiation pattern consists of a single lobe straight up (radiation toward the ground which isn't absorbed is reflected back upward). The radiation pattern and especially the input impedance is affected by its proximity to the ground.

If fed with higher frequencies the antenna input impedance will generally include a reactive part and a different resistive component, requiring use of an antenna tuner. As the frequency increases above the first harmonic, the radiation pattern breaks up into multiple lobes which peak at lower angles relative to the horizon, which is an improvement for long-distance communication for frequencies well-above the loop's second harmonic.

Halo antennas

A halo antenna is often described as a half-wave dipole antenna that has been bent into a circle. Although it could be categorized as a bent dipole, it has the omnidirectional radiation pattern very nearly the same as a small loop. The halo is more efficient than a small loop, since it is a larger antenna at ⁠1/ 2 ⁠ wave in circumference with its disproportionately larger radiation resistance. Because of its much greater radiation resistance, a halo presents a good impedance match to 50 Ohm coaxial cable, and its construction is less demanding than a small loop, since the maker is not compelled to take such extreme care to avoid losses from mediocre conductors and contact resistance.

At ⁠1/ 2 ⁠ wave, the halo antenna is near or on the extreme high limit of the size range for “small” loops, but unlike most oversized small loops, it can be analyzed with simple techniques by treating it as a bent dipole.

Practical use

On the VHF bands and above, the physical diameter of a halo is small enough to be effectively used as a mobile antenna.

The horizontal radiation pattern of a horizontal halo is nearly omnidirectional – to within 3 dB or less – and that can be evened out by making the loop slightly smaller and adding more capacitance between the element tips. Not only will that even out the gain, it will reduce upward radiation, which for VHF is typically wasted: Radiated into space.

Halos pick up less nearby electrical spark interference than monopoles and dipoles – ignition noise from vehicles for example.

Electrical analysis

Although it has a superficially different appearance, the halo antenna can conveniently be analyzed as a dipole (which also has a half-wave radiating part with a high voltage and zero current at its ends) that has been bent into a circle. Simply using dipole results greatly simplifies the calculations and for most properties are the same as a halo. Halo performance can also be modeled with techniques used for similar, moderate-sized "small" transmitting loops, but for brevity, that complicated analysis is often skipped in introductory articles on loop antennas (unfortunately, this typical omission leaves otherwise well-read persons unaware of the properties of "large" small loops).

The halo's gap

Some writers mistakenly consider the gap in the halo antenna's loop to distinguish it from a small loop antenna – since there is no DC connection between the two ends. But that distinction is lost at RF; the close-bent high-voltage ends are capacitively coupled, and the RF current crosses the gap as displacement current. The gap in the halo is electrically equivalent to the tuning capacitor on a small loop, although the incidental capacitance involved is not nearly as large.

Small loops

Small loops are "small" in comparison to their operating wavelength. Contrary to the pattern of large loop antennas, the reception and radiation strength of small loops peaks inside the plane of the loop, rather than broadside (perpendicular) to it.

As with all antennas that are physically much smaller than the operating wavelength, small loop antennas have small radiation resistance which is dwarfed by ohmic losses, resulting in a poor antenna efficiency. They are thus mainly used as receiving antennas at lower frequencies (wavelengths of tens to hundreds of meters). Like a short dipole antenna, the radiation resistance is small. The radiation resistance ${\displaystyle \ R_{\mathsf {rad}}\ }$ is proportional to the square of the area:

${\displaystyle R_{\mathsf {rad}}\approx 31.2{\mathsf {\ k\Omega \ }}\left({\frac {\ N\ A\ }{\lambda ^{2}}}\right)^{2}}$

where A is the area enclosed by the loop, λ is the wavelength, and N is the number of turns of the conductor around the loop.

Because of the higher exponent than linear antennas (loop area squared ≈ perimeter to the 4th power, vs. dipole & monopole length squared = 2nd power) the fall in R_rad with reduced size is more extreme. The ability to increase the radiation resistance R_rad by using multiple turns is analogous to making a dipole out of two or more parallel lines for each dipole arm ("folded dipole").

Small loops have advantages as receiving antennas at frequencies below 10 MHz. Although a small loop's losses can be high, the same loss applies to both the signal and the noise, so the receiving signal-to-noise ratio of a small loop may not suffer at these lower frequencies, where received noise is dominated by atmospheric noise and static rather than receiver-internal noise. The ability to more manageably rotate a smaller antenna may help to maximize the signal and reject interference. Several construction techniques are used to ensure that small receiving loops' null directions are "sharp", including adding broken shielding of the loop arms and keeping the perimeter around ⁠1/ 10 ⁠ wavelength (or ⁠ 1 /4⁠ wave at most). Small transmitting loops' perimeters are instead made as large as feasibly possible, up to ⁠ 1 /3⁠ wave (or even ⁠ 1 /2⁠ if possible), in order to make the best their generally poor efficiency, although doing so sacrifices sharp nulls.

The small loop antenna is also known as a magnetic loop since the response of an electrically small receiving loop is proportional to the rate of change of magnetic flux through the loop. At higher frequencies (or shorter wavelengths), when the antenna is no longer electrically small, the current distribution through the loop may no longer be uniform and the relationship between its response and the incident fields becomes more complicated. In the case of transmission, the fields produced by an electrically small loop are the same as an "infinitesimal magnetic dipole" whose axis is perpendicular to the plane of the loop.

Because of their meager radiation resistance, the properties of small loops tend to more often be intensively optimized than are full-size antennas, and the properties optimized for transmitting are not quite the same as for receiving. With full-size antennas, the reciprocity between transmitting and receiving usually makes the distinctions unimportant, but since a few RF properties important for receiving differ from those for transmitting – particularly below about 10~20 MHz – small loops intended for receiving have slight differences from small transmitting loops. They are discussed separately in following two subsections, although many of the comments apply to both.

Small receiving loops

If the perimeter of a loop antenna is much smaller than the intended operating wavelengths – say ⁠ 1 / 8 ⁠ to ⁠1/ 100 ⁠ of a wavelength – then the antenna is called a small receiving loop, since loop antennas that small are only practical for receiving. Several performance factors, including received power, scale in proportion to the loop's area. For a given loop area, the length of the conductor (and thus its net loss resistance) is minimized if the perimeter is circular, making a circle the optimal shape for small loops. Small receiving loops are typically used below 14 MHz where human-made and natural atmospheric noise dominate. Thus the signal-to-noise ratio of the received signal will not be adversely affected by low efficiency as long as the loop is not excessively small.

A typical diameter of receiving loops with "air centers" is between 30 and 100 cm (1 and 3.5 feet). To increase the magnetic field in the loop and thus its efficiency, while greatly reducing size, the coil of wire is often wound around a ferrite rod magnetic core; this is called a ferrite loop antenna. Such ferrite loop antennas are used in almost all AM broadcast receivers with the notable exception of car radios, since the antenna for the AM band needs to be outside the obstructing metal car chassis.

Small loop antennas are also popular for radio direction finding, in part due to their exceedingly sharp, clear "null" along the loop axis: When the loop axis is aimed directly at the transmitter, the target signal abruptly vanishes.

The radiation resistance R_rad of a small loop is generally much smaller than the loss resistance R_ℓoss due to the conductors composing the loop, leading to a poor antenna efficiency. Consequently, most of the power delivered to a small loop antenna will be converted to heat by the loss resistance, rather than doing useful work pushing out radio waves or gathering them in.

Wasted power is undesirable for a transmitting antenna, however for a receiving antenna, the inefficiency is not important at frequencies below about 15 MHz. At these lower frequencies, atmospheric noise (static) and man-made noise (interference) even a weak signal from an inefficient antenna is far stronger than the internal thermal or Johnson noise generated in the radio receiver's own circuitry, so the weak signal from a loop antenna can be amplified without degrading the signal-to-noise ratio, since both are magnified by the same amplification factor.

For example, at 1 MHz the man-made noise might be 55 dB above the thermal noise floor. If a small loop antenna's loss is 50 dB (as if the antenna included a 50 dB attenuator) the electrical inefficiency of that antenna will have little influence on the receiving system's signal-to-noise ratio.

In contrast, at quieter frequencies at about 20 MHz and above, an antenna with a 50 dB loss could degrade the received signal-to-noise ratio by up to 50 dB, resulting in terrible performance.

However, as frequency rises there is no need to suffer bad performance: At the higher, quieter frequencies, the wavelengths become short enough that a halo antenna is small enough to be feasible – at 20 MHz it's a little less than 8 feet (2.4 m) in diameter, and proportionally shrinks as the frequency increases. So the quieter the rising frequency gets, the more convenient it is to replace an small receiving loop with a larger, but still relatively compact halos. It's mostly a direct substitute for a small receiving loop, but with superior signal reception.

Radiation pattern and polarization

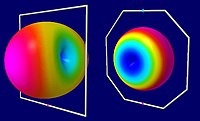
Surprisingly, the radiation and receiving pattern of a small loop is perpendicular to that of a large self resonant loop (whose perimeter is close to one wavelength). Since the loop is much smaller than a wavelength, the current at any one moment is nearly constant round the circumference. By symmetry it can be seen that the voltages induced in the loop windings on opposite sides of the loop, will cancel each other when a perpendicular signal arrives on the loop axis. Therefore, there is a null in that direction. Instead, the radiation pattern peaks in directions lying in the plane of the loop, because signals received from sources in that plane do not quite cancel owing to the phase difference between the arrival of the wave at the near side and far side of the loop. Increasing that phase difference by increasing the size of the loop causes a disproportionately large increase in the radiation resistance, and the resulting antenna efficiency.

Another way of looking at a small loop as an antenna is to consider it simply as an inductive coil coupling to the magnetic field in the direction perpendicular to plane of the coil, according to Ampère's law. Then consider a propagating radio wave also perpendicular to that plane. Since the magnetic (and electric) fields of an electromagnetic wave in free space are transverse (no component in the direction of propagation), it can be seen that this magnetic field and that of a small loop antenna will be at right angles, and thus not coupled. For the same reason, an electromagnetic wave propagating within the plane of the loop, with its magnetic field perpendicular to that plane, is coupled to the magnetic field of the coil. Since the transverse magnetic and electric fields of a propagating electromagnetic wave are at right angles, the electric field of such a wave is also in the plane of the loop, and thus the antenna's polarization (which is always specified as being the orientation of the electric, not the magnetic field) is said to be in that plane.

Thus mounting the loop in a horizontal plane will produce an omnidirectional antenna which is horizontally polarized; mounting the loop vertically yields a vertically polarizated, weakly directional antenna, but with an exceptionally sharp nulls along the axis of the loop. Size criteria that favor loops with a perimeter of ⁠ 1 / 4 ⁠ wave or smaller ensure the sharpness of the loop's receiving null. Small loops intended for transmitting (see below) are designed as large as feasible to improve the marginal radiation resistance, sacrificing the sharp null by using perimeters as large as ⁠ 1 / 3 ⁠~⁠ 1 / 2 ⁠ wave.

Receiver input tuning

Since a small loop antenna is essentially a coil, its electrical impedance is inductive, with an inductive reactance much greater than its radiation resistance. In order to couple to a transmitter or receiver, the inductive reactance is normally canceled with a parallel capacitance. Since a good loop antenna will have a high Q factor (narrow bandwidth), the capacitor must be variable and is adjusted to match the receiver's tuning.

Small loop receiving antennas are also almost always resonated using a parallel plate capacitor, which makes their reception narrow-band, sensitive only to a very specific frequency. This allows the antenna, in conjunction with a (variable) tuning capacitor, to act as a tuned input stage to the receiver's front-end, in lieu of a preselector.

Direction finding with small loops

As long as the loop perimeter is kept below about ⁠ 1 /4⁠ wave, the directional response of small loop antennas includes a sharp null in the direction normal to the plane of the loop, so small loops are favored as compact radio direction finding antennas for long wavelengths.

The procedure is to rotate the loop antenna to find the direction where the signal vanishes – the “null” direction. Since the null occurs at two opposite directions along the axis of the loop, other means must be employed to determine which side of the antenna the “nulled” signal is on. One method is to rely on a second loop antenna located at a second location, or to move the receiver to that other location, thus relying on triangulation.

Instead of triangulation, a second dipole or vertical antenna can be electrically combined with a loop or a loopstick antenna. Called a sense antenna, connecting and matching the second antenna changes the combined radiation pattern to a cardioid, with a null in only one (less precise) direction. The general direction of the transmitter can be determined using the sense antenna, and then disconnecting the sense antenna returns the sharp nulls in the loop antenna pattern, allowing a precise bearing to be determined.

AM broadcast receiving antennas

Small loop antennas are lossy and inefficient for transmitting, but they can be practical receiving antennas in the mediumwave (520–1710 kHz) broadcast band and below, where wavelength-sized antennas are infeasibly large, and the antenna inefficiency is irrelevant, due to large amounts of atmospheric noise.

AM broadcast receivers (and other low frequency radios for the consumer market) typically use small loop antennas, even when a telescoping antenna may be attached for FM reception. A variable capacitor connected across the loop forms a resonant circuit that also tunes the receiver's input stage as that capacitor tracks the main tuning. A multiband receiver may contain tap points along the loop winding in order to tune the loop antenna at widely different frequencies.

In AM radios built prior to the invention of ferrite in the mid-20th century, the antenna might consist of dozens of turns of wire mounted on the back wall of the radio – a planar helical antenna – or a separate, rotatable, furniture-sized rack looped with wire – a frame antenna.

Ferrite

Ferrite loop antennas are made by winding fine wire around a ferrite rod. They are almost universally used in AM broadcast receivers. Other names for this type of antenna are loopstick, ferrite rod antenna or aerial, ferroceptor, or ferrod antenna. Often, at mediumwave and lower shortwave frequencies, Litz wire is used for the winding to reduce skin effect losses. Elaborate “basket weave” patterns are used at all frequencies to reduce inter-winding capacitance in the coil insuring that the loop self-resonance is well above the operating frequency, so that it acts as an electrical inductor that can be resonated with a tuning capacitor, and with a consequent improvement of the loop Q factor.

Inclusion of a magnetically permeable core increases the radiation resistance of a small loop, mitigating the inefficiency due to ohmic losses. Like all small antennas, such antennas are tiny compared to their effective area. A typical AM broadcast radio loop antenna wound on ferrite may have a cross sectional area of only 1 cm (0.16 sq in) at a frequency at which an ideal (lossless) antenna would have an effective area some hundred million times larger. Even accounting for the resistive losses in a ferrite rod antenna, its effective receiving area may exceed the loop's physical area by a factor of 100.

Small transmitting loops

Small transmitting loops are “small” in comparison to a full wavelength, but considerably larger than a “small” receive-only loop. They are typically used on frequencies between 14–30 MHz. Unlike receiving loops, small transmitting loops’ sizes must be scaled-up for longer wavelengths, in order to keep radiation resistance from falling to unusably low levels; their larger sizes blur or erase the otherwise especially sharp nulls small receiving loops provide.

Size, shape, efficiency, and pattern

A transmitting loop usually consists of a single turn of large diameter conductor; they are typically round or octagonal to provide maximum enclosed area for a given perimeter, hence maximizing radiation resistance. The smaller of these loops are much less efficient than the extraordinary performance of full-sized, self-resonant loops, or the moderate efficiency of monopoles, dipoles, and halos, but where space for a full wave loop or a half-wave dipole is not available, small loops can provide adequate communications with low, but tolerable efficiency.

A small transmitting loop antenna with a perimeter of 10% or less of the wavelength will have a relatively constant current distribution along the conductor, and the main lobe will be in the plane of the loop, so they will show the strong null familiar in the radiation pattern of small receiving loops. Loops of any size between 10% and 30% of a wavelength in perimeter, up to almost exactly 50% in circumference, can be built and tuned with series capacitor to resonance but their non-uniform current will reduce or eliminate the small loops' pattern null. A capacitor is required for a circumference less than a half wave, an inductor for loops more than a half wave and less than a full wave.

Loops in the small transmitting loops' size range may have neither the uniform current of very small loops, nor the sinusoidal current of large loops, and thus cannot be analyzed using the assumptions useful for the small receiving loops nor full-wave loop antennas. Performance is most conveniently determined using NEC analysis. Antennas within this size range include the halo (see above) and the G0CWT (Edginton) loop. For brevity, introductory articles on small loop antennas sometimes confine discussion to loops smaller in circumference than ⁠1/ 10 ⁠ wavelength, since for loops with circumferences larger than ⁠1/ 10 ⁠ wave the simplifying assumption of uniform current around the entire loop becomes untenably inaccurate. Since the larger halo also has a simple analysis, moderate-sized small loop antennas and their complicated analysis are often omitted, leaving many otherwise well informed antenna builders in the dark regarding the performance obtainable with moderately small loops.

Use for land-mobile radio

Vertically aligned small loops are used in military land-mobile radio, at frequencies between 3~7 MHz, because of their ability to direct energy upwards, unlike a conventional whip antenna. This enables near vertical incidence skywave (NVIS) communication up to 300 km (190 miles) in mountainous regions. For NVIS a typical radiation efficiency of around 1% is acceptable, because signal paths can be established with 1 W of radiated power or less – feasible when a 100 W transmitter is used.

In military use, the antenna may be built using a one or two conductors 2.5–5 cm (1–2 inches) in diameter. The loop itself is typically 1.8 m (6 feet) in diameter.

Power limits and RF safety

One practical issue with small loops as transmitting antennas is that a small transmitting loop will not only have a very large current going through it, but also has a very high voltage across the capacitor – typically thousands of volts – even when fed with only a few watts of transmitter power. The smaller the loop (in wavelengths) the higher the voltage. This requires a rather expensive and physically large resonating capacitor with a large breakdown voltage, in addition to having minimal dielectric loss (normally requiring an air-gap capacitor or even a vacuum variable capacitor).

Making the loop larger in diameter will lower the gap voltage, as well as improving efficiency, however all other efficiency improvements will tend to increase the gap voltage: Efficiency may be increased by making the loop from a thicker conductor; other measures to lower the conductor's loss resistance include welding or brazing the connections, rather than soldering. But because reducing loss resistance increases the antenna's Q the consequence of better efficiency is even greater voltage across the capacitor at the loop's gap. For a given frequency, a smaller small loop is more dangerous than a larger small loop, and perversely, a comparatively efficient small transmitting loop is more dangerous than an inefficient one.

The RF burn and shock problems raised by capacitive loading of small loops is more serious than for inductive loading of short whips or dipole antennas. The high antenna voltage is generally troublesome only on the upper end of a whip's loading coil, since it is spread across the extended coil length, whereas high voltages on a loop's capacitor plates are (ideally) at maximum over all of the plate surfaces. Further, the high voltage tips of monopoles and dipoles typically are mounted high up and far out of reach, which limits opportunities for radio-frequency burns. In contrast, small loop / “magnetic” antennas better tolerate being mounted close to the ground so all parts of loop antennas, including the high voltage parts, are more often within easy reach.

In summary: The high voltages from high Q pose a greater threat in small loops than most other small antennas, and demand greater caution, even for very low transmit power.

Feeder loops

In addition to other common impedance matching techniques such as a gamma match, small receiving and transmitting loops are sometimes impedance matched by connecting the feedline to an even smaller feeder loop inside the area surrounded by the main loop. Although it may / should still be connected through the ground system, this leaves the main loop with no other DC connection to the transmitter. The feeder loop and the main loop are effectively the primary and secondary coils of a transformer, with power in the near-field inductively coupled from the feed loop into the main loop, which itself is connected to the resonating capacitor and radiates most of the signal power.

If both the main and the feeder loops are single-turn, the impedance transformation ratio of the nested loops is almost exactly the ratio of the areas of the two loops separately, or the square of the ratio of their diameters (assuming they have the same shape). Typical feeder loops are ⁠ 1 / 8 ⁠ to ⁠ 1 / 5 ⁠ the size of the antenna's main loop, which gives transform ratios of 64:1 to 25:1, respectively. Adjusting the proximity and angle of the feeder loop to the main loop, and distorting the feeder's shape, both make small to moderate changes the transform ratio, and allows for fine adjustment of the feedpoint impedance. For main loops with multiple turns, more often used for mediumwave frequencies, the feeder loop can be one or two turns on the same frame as the main loop's turns, in which case the impedance transform ratio is very nearly the square of the ratio of the number of turns on each loop.

Antenna-like non-antenna loops

Some so-called "antennas" look very much like genuine loop antennas, but are designed to couple with the inductive near-field, over distances of 1–2 meters (3–7 feet), rather than to transmit or receive long-distance electromagnetic waves in the radiative far-field. Because of this difference the near-field "antennas" are not radio antennas at all (when correctly functioning for the purpose they are designed for).

Likewise, coupling coils used for inductive charging systems, regardless of whether they are used at low or high radio frequencies, are excluded from this article, since they are not (or ideally, shouldn't be) radio antennas.

RFID coils and induction heating

Inductive heating systems, induction cooking stovetops, and RFID tags and readers all interact by near field magnetic induction rather than far field transmitted waves. So strictly speaking, they are not radio antennas.

Although they are not radio antennas, these systems do operate at radio frequencies, and they involve the use of small magnetic coils, which are called "antennas" in the trade. However, they are more usefully thought of as analogs to the windings in loosely coupled transformers. Although the magnetic coils in these inductive systems sometimes seem indistinguishable from the small loop antennas discussed above, such devices can only operate over short distances, and are specifically designed to avoid transmitting or receiving radio waves. Because inductive heating systems and RFID readers only use near field alternating magnetic fields, their performance criteria are dissimilar to far field radio antennas discussed in this article.

Footnotes

1. The antenna can be described as "self-resonant" in the sense that if you short the antenna terminals, then a current in the loop will be created in response to an electromagnetic wave, and the relative magnitude of that current will be greatly increased around the resonant frequency. The antenna being "resonant" also implies that the input impedance of the antenna, which is reactive at most frequencies, becomes purely resistive (resonant) at this frequency.
2. For loops larger than 1 wavelength perimeter, the directive gain increases slightly up to a perimeter of 1.4 wavelengths, but for larger circular loops the radiation pattern becomes multilobed and the perpendicular radiation vanishes or is greatly diminished.
3. Small loops with circumferences up to ⁠ 1 /3⁠~⁠ 1 /4⁠ wavelength are used for transmitting antennas, although their construction requires fastidious efforts to minimize loss resistance; the practical lower size-limit is somewhere around ⁠ 1 /7⁠~⁠1/ 10 ⁠ wave.
4. ^ An important exception is that radios built for installation inside metal car bodies cannot contain antennas, since their AM reception would be blocked by the metal of the chassis and the dashboard. Car radios must use external antennas, which are essentially never ferrite loops.
5. An antenna's feedpoint is the place where its feedline (RF transmission line) attaches to the radiating part of the antenna.
6. A halo antenna has very roughly 10×~500× greater radiation resistance than ⁠1/ 4 ⁠~⁠1/ 10 ⁠ wave loops, respectively.
7. A halo antenna does not need capacitive end-loading, since the nearly ⁠1/ 2 ⁠ wave circumference halo antenna is already self-resonant. However, since end-capacitance is present even if not needed, to restore resonance the dipole-sized arms must each be trimmed back from the conventional 97% of a quarter-wave.
   Often, the antenna maker cuts the halo ends even shorter than needed to restore resonance, and moves the ends even closer together to increase the end capacitance, to make the halo radiation pattern more like a small loop: Even more nearly omnidirectional, with further reduced vertical radiation (for a horizontal halo).
8. The loss resistance includes not only the DC resistance of the conductor but also its increase due to the skin effect and proximity effect. The loss resistance also includes losses in the ferrite rod, if one is used.
9. Since a halo antenna is a half-wave, it will deliver a strong signal to the receiver – essentially equally strong as a conventional dipole antenna's received signal power.
   A halo's reception pattern is close to that of the small loop it would replace, the major exception being that it will not reproduce small receiving loops' famously sharp nulls. Since halo can be either vertically or horizontally mounted, like the small receiving loop it replaces, it can provide a similar bidirectional or omnidirectional reception pattern, respectively.
   The main drawback of substitute a halo for a small receiving loop is that normal halos can only operate on the band surrounding the single frequency they are sized for: In that regard a halo is not a direct substitute for a small loop. Although a halo will have bandwidth comparable to a dipole near its design frequency, no current design can retune a halo to the wide a range of different frequencies that are obtained from a variably tuned small loop.
10. Since AM broadcast radio is conventionally vertically polarized, the internal antennas of AM radios are loops in the vertical plane (that is, with the loopstick core, around which the loop is wound, horizontally oriented). One can easily demonstrate the directivity of such an antenna by tuning to an AM station (preferably a weaker one) and rotating the radio in all horizontal directions. At a particular orientation (and at 180 degrees from it) the station will be in the direction of the ‘null’, that is, in the direction of the loopstick (normal to the loop). At that point reception of the station will fade out.
11. Although a series capacitor could also be used to cancel the reactive impedance, doing so results in the receiver (or transmitter) seeing a very small (resistive) impedance. On the other hand, a parallel capacitor creates a parallel-type resonance. At resonance, when the capacitor's susceptance cancels the antenna's susceptance, the loop + capacitor tank circuit produces a very large resistive impedance at the feedpoint, thus provides a much larger voltage to the receiver's input stage.
    Note however, that the increased resistance measured at the feedpoint is the result of an impedance transform: The resonant inductor (loop) + capacitor network magnifies all of the loop's different impedances, including its loss resistances, so the loop's feedpoint resistance is not the actual radiation resistance, which is far smaller. (There is no increase in antenna efficiency – no free lunch.)
12. For linear / straight-wire / “electric” antennas, matching using a loading coil also generates high voltages at the antenna end(s) and in the loading coil, however unlike capacitors, the high voltage difference is evenly spread along the length of the coil, and as a precaution it usually is intentionally made physically longer and more slender than the more efficient stubby shape.
13. Soil is closer to being transparent for the magnetic part of radio waves, and more prone to absorb or reflect the electric part of RF waves, which is what linear / “electric” antennas interact with.

References

1. ^ Balanis, Constantine (2005). Antenna Theory (third ed.). Wiley-Interscience. p. 246. ISBN 0-471-66782-X.
2. ^ Silver, H. Ward; et al., eds. (2015). "Chapter 5 – Loop antennas". The ARRL Antenna Book. Newington, CT: The American Radio Relay League. ISBN 978-1-62595-044-4.
3. ^ Balanis, Constantine A. (2016). Antenna Theory: Analysis and design (4th ed.). John Wiley & Sons. ISBN 978-1-118-64206-1.
4. Danzer, Paul (September 2004). "A 6 meter halo". QST Magazine. pp. 37–39.
5. Tildon, Edward P. (December 1956). "Polarization effects in VHF mobile". QST Magazine. pp. 11–13.
6. Straw, R. Dean; et al., eds. (2007). The ARRL Antenna Book. The American Radio Relay League. ISBN 978-0-87259-987-1.
7. Karlquist, Rick (17 Oct 2008). Low band receiving loops (PDF). PacifiCon 2008. Retrieved 2018-04-29 – via n6rk.com.
8. ^ Broyde, F.; Clavelier, E. (January 2023). "The Open-Circuit Voltage of a Planar Wire Loop Antenna Used for Reception". Excem Research Papers in Electronics and Electromagnetics (6). doi:10.5281/zenodo.7498910.
9. Poole, Ian (2003). Newnes guide to radio and communications technology. Elsevier. pp. 113–114. ISBN 0-7506-5612-3.
10. ^ CCIR 258; CCIR 322.
11. Rudge, A.W.; Milne, K.; Olver, A.D.; Knight, P. (1982). Handbook of Antenna Design. Vol. 2. p. 688. ISBN 0-86341-569-5.
12. ^ Dean, Charles E. (1959). Henney, Keith (ed.). Radio Engineering Handbook. New York: McGraw-Hill. ch. 19 p. 21.
13. Snelling, E.C. (1988). Soft Ferrites: Properties and applications (second ed.). Butterworths. p. 303. ISBN 0-408-02760-6.
14. Siwiak, Kai, KE4PT; Findling, Amir, K9CHP (Summer 2012). "How efficient is your loop antenna?" (PDF). The QRP Quarterly – via qsl.net/k4fk.{{cite magazine}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
15. Brogdon, A. (April 2007). Low Profile Amateur Radio: Operating a ham station from almost anywhere (2nd ed.). Newington, CT: American Radio Relay League. ISBN 978-0-87259-974-1.
16. ^ Austin, B.A.; Boswell, A.; Perks, M.A. (1 August 2014). Loss mechanisms in the electrically small loop antenna (PDF). mpoweruk.com (Report). Archived from the original (PDF) on 22 December 2016. Retrieved 4 August 2017.

External links

• Yates, Steve (AA5TB). "Small transmitting loop antennas". Magnetic loop antennas. AA5TB.com. Fort Worth, TX. Retrieved 2022-10-14.{{cite web}}: CS1 maint: numeric names: authors list (link)

• "Small transmitting loop". Antenna calculators. 66pacific.com. Retrieved 2022-10-14. — Online calculator that solves the "Basic equations for a small loop" using formulas from The ARRL Antenna Book, 15th ed.
• "An overview of the Underestimated Magnetic Loop HF Antenna" (PDF). Magnetic loop antennas. www.nonstopsystems.com. Retrieved 2024-01-01. — Extensive Paper by Leigh Turner VK5KLT (SK) on HF Magnetic Loop Antennas.
• "Interactive Magnetic Loop Calculator". Magnetic Loop Calculator. miguelvaca.github.io. Retrieved 2024-01-01. — Interactive Magnetic Loop Calculator by Jose Vaca VK3CPU.

• Radio frequency antenna types
• Wireless tuning and filtering