Misplaced Pages

Markov logic network

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.

A Markov logic network (MLN) is a probabilistic logic which applies the ideas of a Markov network to first-order logic, defining probability distributions on possible worlds on any given domain .

History

In 2002, Ben Taskar, Pieter Abbeel and Daphne Koller introduced relational Markov networks as templates to specify Markov networks abstractly and without reference to a specific domain. Work on Markov logic networks began in 2003 by Pedro Domingos and Matt Richardson. Markov logic networks a popular formalism for statistical relational learning.

Syntax

A Markov logic network consists of a collection of formulas from first-order logic, to each of which is assigned a real number, the weight. The underlying idea is that an interpretation is more likely if it satisfies formulas with positive weights and less likely if it satisfies formulas with negative weights.

For instance, the following Markov logic network codifies how smokers are more likely to be friends with other smokers, and how stress encourages smoking: 2.0 :: s m o k e s ( X ) ← s m o k e s ( Y ) ∧ i n f l u e n c e s ( X , Y ) 0.5 :: s m o k e s ( X ) ← s t r e s s ( X ) {\displaystyle {\begin{array}{lcl}2.0&::&\mathrm {smokes} (X)\leftarrow \mathrm {smokes} (Y)\land \mathrm {influences} (X,Y)\\0.5&::&\mathrm {smokes} (X)\leftarrow \mathrm {stress} (X)\end{array}}}

Semantics

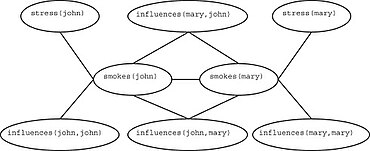
Markov network induced by the theory from Syntax to a two-element domain.

Together with a given domain, a Markov logic network defines a probability distribution on the set of all interpretations of its predicates on the given domain. The underlying idea is that an interpretation is more likely if it satisfies formulas with positive weights and less likely if it satisfies formulas with negative weights.

For any n {\displaystyle n} -ary predicate symbol R {\displaystyle R} that occurs in the Markov logic network and every n {\displaystyle n} -tuple a 1 , … , a n {\displaystyle a_{1},\dots ,a_{n}} of domain elements, R ( a 1 , … , a n ) {\displaystyle R(a_{1},\dots ,a_{n})} is a grounding of R {\displaystyle R} . An interpretation is given by allocating a Boolean truth value (true or false) to each grounding of an element. A true grounding of a formula φ {\displaystyle \varphi } in an interpretation with free variables x 1 , … , x n {\displaystyle x_{1},\dots ,x_{n}} is a variable assignment of x 1 , … , x n {\displaystyle x_{1},\dots ,x_{n}} that makes φ {\displaystyle \varphi } true in that interpretation.

Then the probability of any given interpretation is directly proportional to exp ⁡ ( ∑ j w j n j ) {\displaystyle \exp(\sum _{j}w_{j}n_{j})} , where w j {\displaystyle w_{j}} is the weight of the j {\displaystyle j} -th sentence of the Markov logic network and n j {\displaystyle n_{j}} is the number of its true groundings.

This can also be seen as inducing a Markov network whose nodes are the groundings of the predicates occurring in the Markov logic network. The feature functions of this network are the groundings of the sentences occurring in the Markov logic network, with value e w {\displaystyle e^{w}} if the grounding is true and 1 otherwise (where again w {\displaystyle w} is the weight of the formula).

Inference

The probability distributions induced by Markov logic networks can be queried for the probability of a particular event, given by an atomic formula (marginal inference), possibly conditioned by another atomic formula.

Marginal inference can be performed using standard Markov network inference techniques over the minimal subset of the relevant Markov network required for answering the query. Exact inference is known to be #P-complete in the size of the domain.

In practice, the exact probability is often approximated. Techniques for approximate inference include Gibbs sampling, belief propagation, or approximation via pseudolikelihood.

The class of Markov logic networks which use only two variables in any formula allows for polynomial time exact inference by reduction to weighted model counting.

See also

Resources

  1. ^ Cozman, Fabio Gagliardi (2020), "Languages for Probabilistic Modeling Over Structured and Relational Domains", A Guided Tour of Artificial Intelligence Research, Cham: Springer International Publishing, pp. 247–283, doi:10.1007/978-3-030-06167-8_9, ISBN 978-3-030-06166-1
  2. Taskar, Ben; Abbeel, Pieter; Koller, Daphne (2002-08-01). "Discriminative probabilistic models for relational data". Proceedings of the Eighteenth conference on Uncertainty in artificial intelligence. UAI'02. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.: 485–492. ISBN 978-1-55860-897-9.
  3. Domingos, Pedro (2015). The Master Algorithm: How machine learning is reshaping how we live. p. 246-7.
  4. ^ Richardson, Matthew; Domingos, Pedro (2006). "Markov Logic Networks" (PDF). Machine Learning. 62 (1–2): 107–136. doi:10.1007/s10994-006-5833-1.
  5. Augustine, Eriq (2023). Building Practical Statistical Relational Learning Systems (Thesis). UC Santa Cruz.
  6. ^ Sun, Zhengya; Zhao, Yangyang; Wei, Zhuoyu; Zhang, Wensheng; Wang, Jue (2017). "Scalable learning and inference in Markov logic networks". International Journal of Approximate Reasoning. 82: 39–55. doi:10.1016/j.ijar.2016.12.003. ISSN 0888-613X.
  7. Marra, Giuseppe; Dumančić, Sebastijan; Manhaeve, Robin; De Raedt, Luc (2024-03-01). "From statistical relational to neurosymbolic artificial intelligence: A survey". Artificial Intelligence. 328: 104062. arXiv:2108.11451. doi:10.1016/j.artint.2023.104062. ISSN 0004-3702. This article incorporates text by Giuseppe Marra, Sebastijan Dumančić, Robin Manhaeve and Luc De Raedt available under the CC BY 4.0 license.
  8. Venugopal, Deepak (2017). "Advances in Inference Methods for Markov Logic Networks" (PDF). IEEE Intelligent Informatics Bulletin. 18 (2): 13–19.
  9. Kuzelka, Ondrej (2021-03-29). "Weighted First-Order Model Counting in the Two-Variable Fragment With Counting Quantifiers". Journal of Artificial Intelligence Research. 70: 1281–1307. arXiv:2007.05619. doi:10.1613/jair.1.12320. ISSN 1076-9757.

External links

Categories: