 Diatonic major scale (Ionian mode, I) on C, a "white note" scale
Diatonic major scale (Ionian mode, I) on C, a "white note" scale





 The modern (diatonic) modes on C
The modern (diatonic) modes on C
In music theory, the term mode or modus is used in a number of distinct senses, depending on context.
Its most common use may be described as a type of musical scale coupled with a set of characteristic melodic and harmonic behaviors. It is applied to major and minor keys as well as the seven diatonic modes (including the former as Ionian and Aeolian) which are defined by their starting note or tonic. (Olivier Messiaen's modes of limited transposition are strictly a scale type.) Related to the diatonic modes are the eight church modes or Gregorian modes, in which authentic and plagal forms of scales are distinguished by ambitus and tenor or reciting tone. Although both diatonic and Gregorian modes borrow terminology from ancient Greece, the Greek tonoi do not otherwise resemble their medieval/modern counterparts.
In the Middle Ages the term modus was used to describe both intervals and rhythm. Modal rhythm was an essential feature of the modal notation system of the Notre-Dame school at the turn of the 12th century. In the mensural notation that emerged later, modus specifies the subdivision of the longa.
Outside of Western classical music, "mode" is sometimes used to embrace similar concepts such as Octoechos, maqam, pathet etc. (see § Analogues in different musical traditions below).
Mode as a general concept
Regarding the concept of mode as applied to pitch relationships generally, in 2001 Harold S. Powers proposed that "mode" has "a twofold sense", denoting either a "particularized scale" or a "generalized tune", or both:
"If one thinks of scale and tune as representing the poles of a continuum of melodic predetermination, then most of the area between can be designated one way or the other as being in the domain of mode."
In 1792, Sir Willam Jones applied the term "mode" to the music of "the Persians and the Hindoos". As early as 1271, Amerus applied the concept to cantilenis organicis (lit. "organic songs", most probably meaning "polyphony"). It is still heavily used with regard to Western polyphony before the onset of the common practice period, as for example "modale Mehrstimmigkeit" by Carl Dahlhaus or "Alte Tonarten" of the 16th and 17th centuries found by Bernhard Meier.
The word encompasses several additional meanings. Authors from the 9th century until the early 18th century (e.g., Guido of Arezzo) sometimes employed the Latin modus for interval, or for qualities of individual notes. In the theory of late-medieval mensural polyphony (e.g., Franco of Cologne), modus is a rhythmic relationship between long and short values or a pattern made from them; in mensural music most often theorists applied it to division of longa into 3 or 2 breves.
Modes and scales
A musical scale is a series of pitches in a distinct order.
The concept of "mode" in Western music theory has three successive stages: in Gregorian chant theory, in Renaissance polyphonic theory, and in tonal harmonic music of the common practice period. In all three contexts, "mode" incorporates the idea of the diatonic scale, but differs from it by also involving an element of melody type. This concerns particular repertories of short musical figures or groups of tones within a certain scale so that, depending on the point of view, mode takes on the meaning of either a "particularized scale" or a "generalized tune". Modern musicological practice has extended the concept of mode to earlier musical systems, such as those of Ancient Greek music, Jewish cantillation, and the Byzantine system of octoechoi, as well as to other non-Western types of music.
By the early 19th century, the word "mode" had taken on an additional meaning, in reference to the difference between major and minor keys, specified as "major mode" and "minor mode". At the same time, composers were beginning to conceive "modality" as something outside of the major/minor system that could be used to evoke religious feelings or to suggest folk-music idioms.
Greek modes
Main article: Musical system of ancient GreeceEarly Greek treatises describe three interrelated concepts that are related to the later, medieval idea of "mode": (1) scales (or "systems"), (2) tonos – pl. tonoi – (the more usual term used in medieval theory for what later came to be called "mode"), and (3) harmonia (harmony) – pl. harmoniai – this third term subsuming the corresponding tonoi but not necessarily the converse.
Greek scales


 The three genera of the Dorian octave species on E
The three genera of the Dorian octave species on E
The Greek scales in the Aristoxenian tradition were:
Aristoxenian
scalerough
modern
pitchAristoxenus' description Mixolydian b–b′ hypate hypaton–paramese Lydian c′–c″ parhypate hypaton–trite diezeugmenon Phrygian d′–d″ lichanos hypaton–paranete diezeugmenon Dorian e′–e″ hypate meson–nete diezeugmenon Hypolydian f′–f″ parhypate meson–trite hyperbolaion Hypophrygian g′–g″ lichanos meson–paranete hyperbolaion Common,
Locrian, or
Hypodoriana′–a″ or
a–a′mese–nete hyperbolaion or
proslambnomenos–mese
These names are derived from ancient Greeks' cultural subgroups (Dorians), small regions in central Greece (Locris), and certain Anatolian peoples (Lydia, Phrygia) (not ethnically Greek, but in close contact with them). The association of these ethnic names with the octave species appears to precede Aristoxenus, who criticized their application to the tonoi by the earlier theorists whom he called the "Harmonicists". According to Bélis (2001), he felt that their diagrams, which exhibit 28 consecutive dieses, were
- "... devoid of any musical reality since more than two quarter-tones are never heard in succession."
Depending on the positioning (spacing) of the interposed tones in the tetrachords, three genera of the seven octave species can be recognized. The diatonic genus (composed of tones and semitones), the chromatic genus (semitones and a minor third), and the enharmonic genus (with a major third and two quarter tones or dieses). The framing interval of the perfect fourth is fixed, while the two internal pitches are movable. Within the basic forms, the intervals of the chromatic and diatonic genera were varied further by three and two "shades" (chroai), respectively.
In contrast to the medieval modal system, these scales and their related tonoi and harmoniai appear to have had no hierarchical relationships amongst the notes that could establish contrasting points of tension and rest, although the mese ("middle note") might have functioned as some sort of central, returning tone for the melody.
Tonoi
The term tonos (pl. tonoi) was used in four senses:
- "as note, interval, region of the voice, and pitch. We use it of the region of the voice whenever we speak of Dorian, or Phrygian, or Lydian, or any of the other tones".
Cleonides attributes thirteen tonoi to Aristoxenus, which represent a progressive transposition of the entire system (or scale) by semitone over the range of an octave between the Hypodorian and the Hypermixolydian. According to Cleonides, Aristoxenus's transpositional tonoi were named analogously to the octave species, supplemented with new terms to raise the number of degrees from seven to thirteen. However, according to the interpretation of at least three modern authorities, in these transpositional tonoi the Hypodorian is the lowest, and the Mixolydian next-to-highest – the reverse of the case of the octave species, with nominal base pitches as follows (descending order):
nominal
modern
baseAristoxenian school name F Hypermixolydian (or Hyperphrygian) E High Mixolydian or Hyperiastian E Low Mixolydian or Hyperdorian D Lydian C Low Lydian or Aeolian C Phrygian B Low Phrygian or Iastian B Dorian A Hypolydian G Low Hypolydian or Hypoaeolian G Hypophrygian F Low Hypophrygian or Hypoiastian F Hypodorian
Ptolemy, in his Harmonics, ii.3–11, construed the tonoi differently, presenting all seven octave species within a fixed octave, through chromatic inflection of the scale degrees (comparable to the modern conception of building all seven modal scales on a single tonic). In Ptolemy's system, therefore there are only seven tonoi. Pythagoras also construed the intervals arithmetically (if somewhat more rigorously, initially allowing for 1:1 = Unison, 2:1 = Octave, 3:2 = Fifth, 4:3 = Fourth and 5:4 = Major Third within the octave). In their diatonic genus, these tonoi and corresponding harmoniai correspond with the intervals of the familiar modern major and minor scales. See Pythagorean tuning and Pythagorean interval.
Harmoniai
| Mixolydian | 1⁄4 | 1⁄4 | 2 | 1⁄4 | 1⁄4 | 2 | 1 |
|---|---|---|---|---|---|---|---|
| Lydian | 1⁄4 | 2 | 1⁄4 | 1⁄4 | 2 | 1 | 1⁄4 |
| Phrygian | 2 | 1⁄4 | 1⁄4 | 2 | 1 | 1⁄4 | 1⁄4 |
| Dorian | 1⁄4 | 1⁄4 | 2 | 1 | 1⁄4 | 1⁄4 | 2 |
| Hypolydian | 1⁄4 | 2 | 1 | 1⁄4 | 1⁄4 | 2 | 1⁄4 |
| Hypophrygian | 2 | 1 | 1⁄4 | 1⁄4 | 2 | 1⁄4 | 1⁄4 |
| Hypodorian | 1 | 1⁄4 | 1⁄4 | 2 | 1⁄4 | 1⁄4 | 2 |
In music theory the Greek word harmonia can signify the enharmonic genus of tetrachord, the seven octave species, or a style of music associated with one of the ethnic types or the tonoi named by them.
Particularly in the earliest surviving writings, harmonia is regarded not as a scale, but as the epitome of the stylised singing of a particular district or people or occupation. When the late-6th-century poet Lasus of Hermione referred to the Aeolian harmonia, for example, he was more likely thinking of a melodic style characteristic of Greeks speaking the Aeolic dialect than of a scale pattern. By the late 5th century BC, these regional types are being described in terms of differences in what is called harmonia – a word with several senses, but here referring to the pattern of intervals between the notes sounded by the strings of a lyra or a kithara.
However, there is no reason to suppose that, at this time, these tuning patterns stood in any straightforward and organised relations to one another. It was only around the year 400 that attempts were made by a group of theorists known as the harmonicists to bring these harmoniai into a single system and to express them as orderly transformations of a single structure. Eratocles was the most prominent of the harmonicists, though his ideas are known only at second hand, through Aristoxenus, from whom we learn they represented the harmoniai as cyclic reorderings of a given series of intervals within the octave, producing seven octave species. We also learn that Eratocles confined his descriptions to the enharmonic genus.
Philosophical harmoniai in Plato and Aristotle
In the Republic, Plato uses the term inclusively to encompass a particular type of scale, range and register, characteristic rhythmic pattern, textual subject, etc. Plato held that playing music in a particular harmonia would incline one towards specific behaviors associated with it, and suggested that soldiers should listen to music in Dorian or Phrygian harmoniai to help harden them but avoid music in Lydian, Mixolydian, or Ionian harmoniai, for fear of being softened. Plato believed that a change in the musical modes of the state would cause a wide-scale social revolution.
The philosophical writings of Plato and Aristotle (c. 350 BC) include sections that describe the effect of different harmoniai on mood and character formation. For example, Aristotle stated in his Politics:
But melodies themselves do contain imitations of character. This is perfectly clear, for the harmoniai have quite distinct natures from one another, so that those who hear them are differently affected and do not respond in the same way to each. To some, such as the one called Mixolydian, they respond with more grief and anxiety, to others, such as the relaxed harmoniai, with more mellowness of mind, and to one another with a special degree of moderation and firmness, Dorian being apparently the only one of the harmoniai to have this effect, while Phrygian creates ecstatic excitement. These points have been well expressed by those who have thought deeply about this kind of education; for they cull the evidence for what they say from the facts themselves.
Aristotle continues by describing the effects of rhythm, and concludes about the combined effect of rhythm and harmonia (viii:1340b:10–13):
From all this it is clear that music is capable of creating a particular quality of character in the soul, and if it can do that, it is plain that it should be made use of, and that the young should be educated in it.
The word ethos (ἦθος) in this context means "moral character", and Greek ethos theory concerns the ways that music can convey, foster, and even generate ethical states.
Melos
Some treatises also describe "melic" composition (μελοποιΐα), "the employment of the materials subject to harmonic practice with due regard to the requirements of each of the subjects under consideration" – which, together with the scales, tonoi, and harmoniai resemble elements found in medieval modal theory. According to Aristides Quintilianus, melic composition is subdivided into three classes: dithyrambic, nomic, and tragic. These parallel his three classes of rhythmic composition: systaltic, diastaltic and hesychastic. Each of these broad classes of melic composition may contain various subclasses, such as erotic, comic and panegyric, and any composition might be elevating (diastaltic), depressing (systaltic), or soothing (hesychastic).
According to Thomas J. Mathiesen, music as a performing art was called melos, which in its perfect form (μέλος τέλειον) comprised not only the melody and the text (including its elements of rhythm and diction) but also stylized dance movement. Melic and rhythmic composition (respectively, μελοποιΐα and ῥυθμοποιΐα) were the processes of selecting and applying the various components of melos and rhythm to create a complete work. According to Aristides Quintilianus:
And we might fairly speak of perfect melos, for it is necessary that melody, rhythm and diction be considered so that the perfection of the song may be produced: in the case of melody, simply a certain sound; in the case of rhythm, a motion of sound; and in the case of diction, the meter. The things contingent to perfect melos are motion-both of sound and body-and also chronoi and the rhythms based on these.
Western Church

Tonaries, lists of chant titles grouped by mode, appear in western sources around the turn of the 9th century. The influence of developments in Byzantium, from Jerusalem and Damascus, for instance the works of Saints John of Damascus (d. 749) and Cosmas of Maiouma, are still not fully understood. The eight-fold division of the Latin modal system, in a four-by-two matrix, was certainly of Eastern provenance, originating probably in Syria or even in Jerusalem, and was transmitted from Byzantine sources to Carolingian practice and theory during the 8th century. However, the earlier Greek model for the Carolingian system was probably ordered like the later Byzantine oktōēchos, that is, with the four principal (authentic) modes first, then the four plagals, whereas the Latin modes were always grouped the other way, with the authentics and plagals paired.
The 6th-century scholar Boethius had translated Greek music theory treatises by Nicomachus and Ptolemy into Latin. Later authors created confusion by applying mode as described by Boethius to explain plainchant modes, which were a wholly different system. In his De institutione musica, book 4 chapter 15, Boethius, like his Hellenistic sources, twice used the term harmonia to describe what would likely correspond to the later notion of "mode", but also used the word "modus" – probably translating the Greek word τρόπος (tropos), which he also rendered as Latin tropus – in connection with the system of transpositions required to produce seven diatonic octave species, so the term was simply a means of describing transposition and had nothing to do with the church modes.
Later, 9th-century theorists applied Boethius's terms tropus and modus (along with "tonus") to the system of church modes. The treatise De Musica (or De harmonica institutione) of Hucbald synthesized the three previously disparate strands of modal theory: chant theory, the Byzantine oktōēchos and Boethius's account of Hellenistic theory. The late-9th- and early 10th-century compilation known as the Alia musica imposed the seven octave transpositions, known as tropus and described by Boethius, onto the eight church modes, but its compilator also mentions the Greek (Byzantine) echoi translated by the Latin term sonus. Thus, the names of the modes became associated with the eight church tones and their modal formulas – but this medieval interpretation does not fit the concept of the ancient Greek harmonics treatises. The modern understanding of mode does not reflect that it is made of different concepts that do not all fit.

According to Carolingian theorists the eight church modes, or Gregorian modes, can be divided into four pairs, where each pair shares the "final" note and the four notes above the final, but they have different intervals concerning the species of the fifth. If the octave is completed by adding three notes above the fifth, the mode is termed authentic, but if the octave is completed by adding three notes below, it is called plagal (from Greek πλάγιος, "oblique, sideways"). Otherwise explained: if the melody moves mostly above the final, with an occasional cadence to the sub-final, the mode is authentic. Plagal modes shift range and also explore the fourth below the final as well as the fifth above. In both cases, the strict ambitus of the mode is one octave. A melody that remains confined to the mode's ambitus is called "perfect"; if it falls short of it, "imperfect"; if it exceeds it, "superfluous"; and a melody that combines the ambituses of both the plagal and authentic is said to be in a "mixed mode".
Although the earlier (Greek) model for the Carolingian system was probably ordered like the Byzantine oktōēchos, with the four authentic modes first, followed by the four plagals, the earliest extant sources for the Latin system are organized in four pairs of authentic and plagal modes sharing the same final: protus authentic/plagal, deuterus authentic/plagal, tritus authentic/plagal, and tetrardus authentic/plagal.
Each mode has, in addition to its final, a "reciting tone", sometimes called the "dominant". It is also sometimes called the "tenor", from Latin tenere "to hold", meaning the tone around which the melody principally centres. The reciting tones of all authentic modes began a fifth above the final, with those of the plagal modes a third above. However, the reciting tones of modes 3, 4, and 8 rose one step during the 10th and 11th centuries with 3 and 8 moving from B to C (half step) and that of 4 moving from G to A (whole step).

After the reciting tone, every mode is distinguished by scale degrees called "mediant" and "participant". The mediant is named from its position between the final and reciting tone. In the authentic modes it is the third of the scale, unless that note should happen to be B, in which case C substitutes for it. In the plagal modes, its position is somewhat irregular. The participant is an auxiliary note, generally adjacent to the mediant in authentic modes and, in the plagal forms, coincident with the reciting tone of the corresponding authentic mode (some modes have a second participant).
Only one accidental is used commonly in Gregorian chant – B may be lowered by a half-step to B♭. This usually (but not always) occurs in modes V and VI, as well as in the upper tetrachord of IV, and is optional in other modes except III, VII and VIII.
| Mode | I (Dorian) | II (Hypodorian) | III (Phrygian) | IV (Hypophrygian) | V (Lydian) | VI (Hypolydian) | VII (Mixolydian) | VIII (Hypomixolydian) |
|---|---|---|---|---|---|---|---|---|
| in Italian music until 17th century |
primi toni | secundi toni | terzi toni | quarti toni | quinti toni | sexti toni | septimi toni | octavi toni |
| Final | D (=re) | D | E (=mi) | E | F (=fa) | F | G (=sol) | G |
| Dominant | A (=la) | F | B (=si) or C (=do) | G or A | C | A | D | B or C |
In 1547, the Swiss theorist Henricus Glareanus published the Dodecachordon, in which he solidified the concept of the church modes, and added four additional modes: the Aeolian (mode 9), Hypoaeolian (mode 10), Ionian (mode 11), and Hypoionian (mode 12). A little later in the century, the Italian Gioseffo Zarlino at first adopted Glarean's system in 1558, but later (1571 and 1573) revised the numbering and naming conventions in a manner he deemed more logical, resulting in the widespread promulgation of two conflicting systems.
Zarlino's system reassigned the six pairs of authentic–plagal mode numbers to finals in the order of the natural hexachord, C–D–E–F–G–A, and transferred the Greek names as well, so that modes 1 through 8 now became C-authentic to F-plagal, and were now called by the names Dorian to Hypomixolydian. The pair of G modes were numbered 9 and 10 and were named Ionian and Hypoionian, while the pair of A modes retained both the numbers and names (11, Aeolian, and 12 Hypoaeolian) of Glarean's system. While Zarlino's system became popular in France, Italian composers preferred Glarean's scheme because it retained the traditional eight modes, while expanding them. Luzzasco Luzzaschi was an exception in Italy, in that he used Zarlino's new system.
In the late-18th and 19th centuries, some chant reformers (notably the editors of the Mechlin, Pustet-Ratisbon (Regensburg), and Rheims-Cambrai Office-Books, collectively referred to as the Cecilian Movement) renumbered the modes once again, this time retaining the original eight mode numbers and Glareanus's modes 9 and 10, but assigning numbers 11 and 12 to the modes on the final B, which they named Locrian and Hypolocrian (even while rejecting their use in chant). The Ionian and Hypoionian modes (on C) become in this system modes 13 and 14.
Given the confusion between ancient, medieval, and modern terminology, "today it is more consistent and practical to use the traditional designation of the modes with numbers one to eight", using Roman numeral (I–VIII), rather than using the pseudo-Greek naming system. Medieval terms, first used in Carolingian treatises, later in Aquitanian tonaries, are still used by scholars today: the Greek ordinals ("first", "second", etc.) transliterated into the Latin alphabet protus (πρῶτος), deuterus (δεύτερος), tritus (τρίτος), and tetrardus (τέταρτος). In practice they can be specified as authentic or as plagal like "protus authentus / plagalis".

Use
A mode indicated a primary pitch (a final), the organization of pitches in relation to the final, the suggested range, the melodic formulas associated with different modes, the location and importance of cadences, and the affect (i.e., emotional effect/character). Liane Curtis writes that "Modes should not be equated with scales: principles of melodic organization, placement of cadences, and emotional affect are essential parts of modal content" in Medieval and Renaissance music.
Dahlhaus lists "three factors that form the respective starting points for the modal theories of Aurelian of Réôme, Hermannus Contractus, and Guido of Arezzo":
- the relation of modal formulas to the comprehensive system of tonal relationships embodied in the diatonic scale
- the partitioning of the octave into a modal framework
- the function of the modal final as a relational center.
The oldest medieval treatise regarding modes is Musica disciplina by Aurelian of Réôme (dating from around 850) while Hermannus Contractus was the first to define modes as partitionings of the octave. However, the earliest Western source using the system of eight modes is the Tonary of St Riquier, dated between about 795 and 800.
Various interpretations of the "character" imparted by the different modes have been suggested. Three such interpretations, from Guido of Arezzo (995–1050), Adam of Fulda (1445–1505), and Juan de Espinosa Medrano (1632–1688), follow:
| Name | Mode | D'Arezzo | Fulda | Espinosa | Example chant |
|---|---|---|---|---|---|
| Dorian | I | serious | any feeling | happy, taming the passions | Veni sancte spiritus |
| Hypodorian | II | sad | sad | serious and tearful | Iesu dulcis amor meus |
| Phrygian | III | mystic | vehement | inciting anger | Kyrie, fons bonitatis |
| Hypophrygian | IV | harmonious | tender | inciting delights, tempering fierceness | Conditor alme siderum |
| Lydian | V | happy | happy | happy | Salve Regina |
| Hypolydian | VI | devout | pious | tearful and pious | Ubi caritas |
| Mixolydian | VII | angelical | of youth | uniting pleasure and sadness | Introibo |
| Hypomixolydian | VIII | perfect | of knowledge | very happy | Ad cenam agni providi |
Modern modes
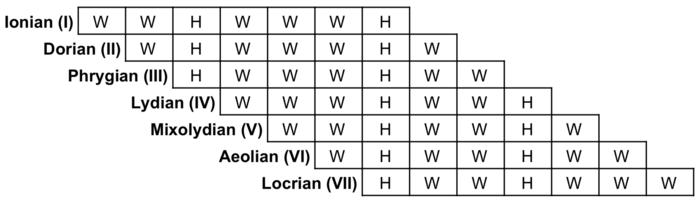
Modern Western modes use the same set of notes as the major scale, in the same order, but starting from one of its seven degrees in turn as a tonic, and so present a different sequence of whole and half steps. With the interval sequence of the major scale being W–W–H–W–W–W–H, where "W" means a whole tone (whole step) and "H" means a semitone (half step), it is thus possible to generate the following modes:
| Mode | Tonic relative to major scale |
Interval sequence | Example |
|---|---|---|---|
| Ionian | I | W–W–H–W–W–W–H | C–D–E–F–G–A–B–C |
| Dorian | ii | W–H–W–W–W–H–W | D–E–F–G–A–B–C–D |
| Phrygian | iii | H–W–W–W–H–W–W | E–F–G–A–B–C–D–E |
| Lydian | IV | W–W–W–H–W–W–H | F–G–A–B–C–D–E–F |
| Mixolydian | V | W–W–H–W–W–H–W | G–A–B–C–D–E–F–G |
| Aeolian | vi | W–H–W–W–H–W–W | A–B–C–D–E–F–G–A |
| Locrian | vii | H–W–W–H–W–W–W | B–C–D–E–F–G–A–B |
For the sake of simplicity, the examples shown above are formed by natural notes (also called "white notes", as they can be played using the white keys of a piano keyboard). However, any transposition of each of these scales is a valid example of the corresponding mode. In other words, transposition preserves mode.
Although the names of the modern modes are Greek and some have names used in ancient Greek theory for some of the harmoniai, the names of the modern modes are conventional and do not refer to the sequences of intervals found even in the diatonic genus of the Greek octave species sharing the same name.
Analysis
| This section does not cite any sources. Please help improve this section by adding citations to reliable sources. Unsourced material may be challenged and removed. (January 2020) (Learn how and when to remove this message) |
Each mode has characteristic intervals and chords that give it its distinctive sound. The following is an analysis of each of the seven modern modes. The examples are provided in a key signature with no sharps or flats (scales composed of natural notes).
Ionian (I)
The Ionian mode is the modern major scale. The example composed of natural notes begins on C, and is also known as the C-major scale:
 The modern Ionian mode on C
The modern Ionian mode on C
| Natural notes | C | D | E | F | G | A | B | C |
|---|---|---|---|---|---|---|---|---|
| Interval from C | P1 | M2 | M3 | P4 | P5 | M6 | M7 | P8 |
- Tonic triad: C major
- Tonic seventh chord: C
- Dominant triad: G (in modern tonal thinking, the fifth or dominant scale degree, which in this case is G, is the next-most important chord root after the tonic)
- Seventh chord on the dominant: G (a dominant seventh chord, so-called because of its position in this – and only this – modal scale)
Dorian (II)
The Dorian mode is the second mode. The example composed of natural notes begins on D:
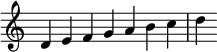 The modern Dorian mode on D
The modern Dorian mode on D
| Natural notes | D | E | F | G | A | B | C | D |
|---|---|---|---|---|---|---|---|---|
| Interval from D | P1 | M2 | m3 | P4 | P5 | M6 | m7 | P8 |
The Dorian mode is very similar to the modern natural minor scale (see Aeolian mode below). The only difference with respect to the natural minor scale is in the sixth scale degree, which is a major sixth (M6) above the tonic, rather than a minor sixth (m6).
- Tonic triad: Dm
- Tonic seventh chord: Dm
- Dominant triad: Am
- Seventh chord on the dominant: Am (a minor seventh chord)
Phrygian (III)
The Phrygian mode is the third mode. The example composed of natural notes starts on E:
 The modern Phrygian mode on E
The modern Phrygian mode on E
| Natural notes | E | F | G | A | B | C | D | E |
|---|---|---|---|---|---|---|---|---|
| Interval from E | P1 | m2 | m3 | P4 | P5 | m6 | m7 | P8 |
The Phrygian mode is very similar to the modern natural minor scale (see Aeolian mode below). The only difference with respect to the natural minor scale is in the second scale degree, which is a minor second (m2) above the tonic, rather than a major second (M2).
- Tonic triad: Em
- Tonic seventh chord: Em
- Dominant triad: Bdim
- Seventh chord on the dominant: B (a half-diminished seventh chord)
Lydian (IV)
The Lydian mode is the fourth mode. The example composed of natural notes starts on F:
 The modern Lydian mode on F
The modern Lydian mode on F
| Natural notes | F | G | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|
| Interval from F | P1 | M2 | M3 | A4 | P5 | M6 | M7 | P8 |
The single tone that differentiates this scale from the major scale (Ionian mode) is its fourth degree, which is an augmented fourth (A4) above the tonic (F), rather than a perfect fourth (P4).
- Tonic triad: F
- Tonic seventh chord: F
- Dominant triad: C
- Seventh chord on the dominant: C (a major seventh chord)
Mixolydian (V)
The Mixolydian mode is the fifth mode. The example composed of natural notes begins on G:
 The modern Mixolydian mode on G
The modern Mixolydian mode on G
| Natural notes | G | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|---|
| Interval from G | P1 | M2 | M3 | P4 | P5 | M6 | m7 | P8 |
The single tone that differentiates this scale from the major scale (Ionian mode) is its seventh degree, which is a minor seventh (m7) above the tonic (G), rather than a major seventh (M7). Therefore, the seventh scale degree becomes a subtonic to the tonic because it is now a whole tone lower than the tonic, in contrast to the seventh degree in the major scale, which is a semitone tone lower than the tonic (leading-tone).
- Tonic triad: G
- Tonic seventh chord: G (the dominant seventh chord in this mode is the seventh chord built on the tonic degree)
- Dominant triad: Dm
- Seventh chord on the dominant: Dm (a minor seventh chord)
Aeolian (VI)
The Aeolian mode is the sixth mode. It is also called the natural minor scale. The example composed of natural notes begins on A, and is also known as the A natural-minor scale:
 The modern Aeolian mode on A
The modern Aeolian mode on A
| Natural notes | A | B | C | D | E | F | G | A |
|---|---|---|---|---|---|---|---|---|
| Interval from A | P1 | M2 | m3 | P4 | P5 | m6 | m7 | P8 |
- Tonic triad: Am
- Tonic seventh chord: Am
- Dominant triad: Em
- Seventh chord on the dominant: Em (a minor seventh chord)
Locrian (VII)
The Locrian mode is the seventh mode. The example composed of natural notes begins on B:
 The modern Locrian mode on B
The modern Locrian mode on B
| Natural notes | B | C | D | E | F | G | A | B |
|---|---|---|---|---|---|---|---|---|
| Interval from B | P1 | m2 | m3 | P4 | d5 | m6 | m7 | P8 |
The distinctive scale degree here is the diminished fifth (d5). This makes the tonic triad diminished, so this mode is the only one in which the chords built on the tonic and dominant scale degrees have their roots separated by a diminished, rather than perfect, fifth. Similarly the tonic seventh chord is half-diminished.
- Tonic triad: Bdim or B°
- Tonic seventh chord: Bm or B
- Dominant triad: F
- Seventh chord on the dominant: FM (a major seventh chord)
Summary
The modes can be arranged in the following sequence, which follows the circle of fifths. In this sequence, each mode has one more lowered interval relative to the tonic than the mode preceding it. Thus, taking Lydian as reference, Ionian (major) has a lowered fourth; Mixolydian, a lowered fourth and seventh; Dorian, a lowered fourth, seventh, and third; Aeolian (natural minor), a lowered fourth, seventh, third, and sixth; Phrygian, a lowered fourth, seventh, third, sixth, and second; and Locrian, a lowered fourth, seventh, third, sixth, second, and fifth. Put another way, the augmented fourth of the Lydian mode has been reduced to a perfect fourth in Ionian, the major seventh in Ionian to a minor seventh in Mixolydian, etc.
| Mode | White note |
Intervals with respect to the tonic | |||||||
|---|---|---|---|---|---|---|---|---|---|
| unison | second | third | fourth | fifth | sixth | seventh | octave | ||
| Lydian | F | perfect | major | major | augmented | perfect | major | major | perfect |
| Ionian | C | perfect | |||||||
| Mixolydian | G | minor | |||||||
| Dorian | D | minor | |||||||
| Aeolian | A | minor | |||||||
| Phrygian | E | minor | |||||||
| Locrian | B | diminished | |||||||
The first three modes are sometimes called major, the next three minor, and the last one diminished (Locrian), according to the quality of their tonic triads. The Locrian mode is traditionally considered theoretical rather than practical because the triad built on the first scale degree is diminished. Because diminished triads are not consonant they do not lend themselves to cadential endings and cannot be tonicized according to traditional practice.
- The Ionian mode corresponds to the major scale. Scales in the Lydian mode are major scales with an augmented fourth. The Mixolydian mode corresponds to the major scale with a minor seventh.
- The Aeolian mode is identical to the natural minor scale. The Dorian mode corresponds to the natural minor scale with a major sixth. The Phrygian mode corresponds to the natural minor scale with a minor second.
- The Locrian is neither a major nor a minor mode because, although its third scale degree is minor, the fifth degree is diminished instead of perfect. For this reason it is sometimes called a "diminished" scale, though in jazz theory this term is also applied to the octatonic scale. This interval is enharmonically equivalent to the augmented fourth found between scale degrees 1 and 4 in the Lydian mode and is also referred to as the tritone.
Use
Use and conception of modes or modality today is different from that in early music. As Jim Samson explains, "Clearly any comparison of medieval and modern modality would recognize that the latter takes place against a background of some three centuries of harmonic tonality, permitting, and in the 19th century requiring, a dialogue between modal and diatonic procedure". Indeed, when 19th-century composers revived the modes, they rendered them more strictly than Renaissance composers had, to make their qualities distinct from the prevailing major-minor system. Renaissance composers routinely sharped leading tones at cadences and lowered the fourth in the Lydian mode.
The Ionian, or Iastian, mode is another name for the major scale used in much Western music. The Aeolian forms the base of the most common Western minor scale; in modern practice the Aeolian mode is differentiated from the minor by using only the seven notes of the Aeolian mode. By contrast, minor mode compositions of the common practice period frequently raise the seventh scale degree by a semitone to strengthen the cadences, and in conjunction also raise the sixth scale degree by a semitone to avoid the awkward interval of an augmented second. This is particularly true of vocal music.
Traditional folk music provides countless examples of modal melodies. For example, Irish traditional music makes extensive usage not only of the major and minor (Aeolian) modes, but also the Mixolydian and Dorian modes. Within the context of Irish traditional music, the tunes are most commonly played in the keys of G-Major/A-Dorian/D-Mixolydian/E-Aeolian (minor) and D-Major/E-Dorian/A-Mixolydian/B-Aeolian (minor). Some Irish music is written in A-Major/F#-Aeolian (minor), with B-Dorian and E-Mixolydian tunes not being completely unheard of. Rarer still are Irish tunes in E-Major/F#-Dorian/B-Mixolydian.
In some regions of Ireland, such as the west-central coast area of counties Galway and Clare, “flat” keys are far more prevalent than in other areas. Instruments will be constructed or pitched accordingly to allow for modal playing in C-Major/D-Dorian/G-Mixolydian or F-Major/G-Dorian/C-Mixolydian/D-Aeolian (minor), with some rare exceptions in Eb-Major/C-minor being played regionally. Some tunes are even composed in Bb-Major, with modulating sections in F-Mixolydian. A-minor is less popularly played in the region, despite the localised prevalence of tunes in C-Major and related modes. Much Flamenco music is in the Phrygian mode, though frequently with the third and seventh degrees raised by a semitone.
Zoltán Kodály, Gustav Holst, and Manuel de Falla use modal elements as modifications of a diatonic background, while modality replaces diatonic tonality in the music of Claude Debussy and Béla Bartók.
Other types
While the term "mode" is still most commonly understood to refer to Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, or Locrian modes in the diatonic scale; in modern music theory the word "mode" is also often used differently, to mean scales other than the diatonic. This is seen, for example, in melodic minor scale harmony, which is based on the seven rotations of the ascending melodic minor scale, yielding some interesting scales as shown below. The "chord" row lists tetrads that can be built from the pitches in the given mode (in jazz notation, the symbol Δ is for a major seventh).
Since Dorian mode is the “middle” mode, we compare it with other modes:
(♯ and ♭ are dual, 2 and 7 are dual, 3 and 6 are dual, 4 and 5 are dual)
Dorian is self-dual, Mixolydian mode and Aeolian mode are dual, Ionian mode and Phrygian mode are dual, etc.
characteristic
scale notesdual scale
characteristicsimplied mode ♯3 ··· ··· ··· Mixolydian mode ♯3 ♭6 Aeolian mode (natural minor and descending melodic minor) ♯3 ♯7 ··· ··· ··· Ionian mode (natural major and ascending melodic major) ♯3 ♯7 ♭2 ♭6 Phrygian mode ♯3 ♯4 ♯7 ··· ··· ··· Lydian mode ♯3 ♯4 ♯7 ♭2 ♭5 ♭6 Locrian mode ♯3 ♯4 ♯5 ♯7 ··· ··· ··· Lydian augmented scale ♯3 ♯4 ♯5 ♯7 ♭2 ♭4 ♭5 ♭6 Altered scale ♯7 ··· ··· ··· Jazz minor scale (ascending melodic minor) ♯7 ♭2 Dorian ♭2 scale ♯3 ♯4 ··· ··· ··· Acoustic scale ♯3 ♯4 ♭5 ♭6 Half diminished scale ♯3 ♯4 ♭6 ··· ··· ··· Lydian dominant ♭6 scale ♯3 ♯4 ♭6 ♯3 ♭5 ♭6 Major Locrian scale ♯3 ♯7 ♭2 ··· ··· ··· ? (Ionian ♭2 scale?) ♯3 ♯7 ♭2 ♯7 ♭2 ♭6 Neapolitan minor scale ♯3 ♯4 ♭2 ··· ··· ··· Romanian major scale ♯3 ♯4 ♭2 ♯7 ♭5 ♭6 ? ♯3 ♯4 ♯7 ♭2 ♭6 ··· ··· ··· ? ♯3 ♯4 ♯7 ♭2 ♭6 ♯3 ♯7 ♭2 ♭5 ♭6 Persian scale ♯4 ··· ··· ··· Ukrainian Dorian scale (Dorian harmonic scale?) ♯4 ♭5 ? (Dorian harmonic scale?) ♯3 ♭2 ··· ··· ··· ? (Mixolydian harmonic scale?) ♯3 ♭2 ♯7 ♭6 ? (Aeolian harmonic scale?) (harmonic minor) ♯3 ♯7 ♭6 ··· ··· ··· ? (Ionian harmonic scale?) (harmonic major) ♯3 ♯7 ♭6 ♯3 ♭2 ♭6 Phrygian dominant scale (Phrygian harmonic scale?) ♯4 ♯7 ··· ··· ··· ? (Lydian harmonic scale?) ♯4 ♯7 ♭2 ♭5 ? (Locrian harmonic scale?) ♯4 ♯7 ♭6 ··· ··· ··· Hungarian minor scale ♯4 ♯7 ♭6 ♯3 ♭2 ♭5 Oriental mode ♯3 ♭6 Aeolian dominant scale (descending melodic major) (self-dual) ♯7 ♭2 Neapolitan major scale (self-dual) ♯3 ♯7 ♭2 ♭6 Double harmonic scale (self-dual)
Or remove two diatonic notes to get pentatonic scale:
removed
scale notesaltered
scale notesimplied pentatonic scale implied classical Chinese scale 3 6 ··· suspended pentatonic scale 商 (shāng) mode (self-dual) 3 7 ··· blues major pentatonic scale 徵 (zhǐ) mode 2 6 ··· minor pentatonic scale 羽 (yǔ) mode 4 7 ♯3 major pentatonic scale 宮 (gōng) mode 2 5 ♭6 blues minor pentatonic scale 角 (jué) mode
Scales that are called “harmonic” contain all seven types of seventh chords (like the harmonic major scale and the harmonic minor scale).
e.g. for Dorian ♯4:
- 1st: Minor seventh chord
- 2nd: Dominant seventh chord
- 3rd: Major seventh chord
- 4th (start with the ♯4): Diminished seventh chord
- 5th: Minor major seventh chord
- 6th: Half-diminished seventh chord
- 7th: Augmented major seventh chord
and for Dorian ♭5:
- 1st: Half-diminished seventh chord
- 2nd: Minor seventh chord
- 3rd: Minor major seventh chord
- 4th: Dominant seventh chord
- 5th (start with the ♭5): Augmented major seventh chord
- 6th: Diminished seventh chord
- 7th: Major seventh chord
In contrast, the original Dorian mode (also the natural major scale and the natural minor scale) does not contain minor major seventh chord and augmented major seventh chord and diminished seventh chord.
| type | in a major key | in a minor key |
|---|---|---|
| natural | Ionian (start with C, use all white keys) | Aeolian (start with A, use all white keys) |
| harmonic | ♭6 | ♯7 |
| melodic | ascending: same as natural / descending: ♭6, ♭7 | ascending: ♯6, ♯7 / descending: same as natural |
The Dorian mode, and Aeolian dominant scale (Dorian ♯3 ♭6 scale), and Neapolitan major scale (Dorian ♭2 ♯7 scale), and double harmonic scale (Dorian ♭2 ♯3 ♭6 ♯7 scale), are all self-dual. However, there are no harmonic scales that are self-dual. From that, we can list the scales and the triad qualities and the seventh chord qualities in each scale as degrees of Dorian mode and Aeolian dominant scale (Dorian ♯3 ♭6 scale) and Neapolitan major scale (Dorian ♭2 ♯7 scale) and double harmonic scale (Dorian ♭2 ♯3 ♭6 ♯7 scale) and the two types of Dorian harmonic scale:
(for Dorian mode and Aeolian dominant scale and Neapolitan major scale and double harmonic scale, the 2nd / 7th scales, the 3rd / 6th scales, the 4th / 5th scales, are dual scales, and for the scale of a type of Dorian harmonic scale, its dual is the 2nd / 7th scale, the 3rd / 6th scale, the 4th / 5th scale, of another Dorian harmonic scale).
| scale | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th |
|---|---|---|---|---|---|---|---|
| Dorian mode | Dorian mode | Phrygian mode | Lydian mode | Mixolydian mode | Aeolian mode, natural minor, descending melodic minor |
Locrian mode | Ionian mode, natural major, ascending melodic major |
| Aeolian dominant scale, Dorian ♯3 ♭6 scale |
Aeolian dominant scale, descending melodic major, Aeolian ♯3 scale, Mixolydian ♭6 scale, Hindu scale, (Dorian ♯3 ♭6 scale) |
half diminished scale, Locrian ♮2 scale, Aeolian ♭5 scale |
altered scale, altered dominant scale, super Locrian scale, Locrian ♭4 scale |
jazz minor scale, ascending melodic minor |
Dorian ♭2 scale, Phrygian ♮6 scale |
Lydian augmented scale, Lydian ♯5 scale |
acoustic scale, overtone scale, Lydian dominant scale, Lydian ♭7 scale, Mixolydian ♯4 scale |
| Neapolitan major scale, Dorian ♭2 ♯7 scale |
Neapolitan major scale, (Dorian ♭2 ♯7 scale) |
leading whole tone scale, Lydian augmented ♯6 scale |
Lydian augmented dominant scale | Lydian dominant ♭6 | major Locrian scale | half-diminished ♭4 scale, altered dominant ♯2 scale |
altered dominant |
| double harmonic scale, Dorian ♭2 ♯3 ♭6 ♯7 scale |
double harmonic scale, double harmonic major scale, (Dorian ♭2 ♯3 ♭6 ♯7 scale) |
Lydian ♯2 ♯6 scale | Ultraphrygian scale | Hungarian minor scale, double harmonic minor scale, Gypsy minor scale |
Oriental mode | Ionian ♯2 ♯5 scale | Locrian |
| Dorian harmonic (♯4) scale | Ukrainian Dorian scale, Romanian minor scale, altered Dorian scale, Dorian harmonic (♯4) scale |
Phrygian dominant scale, altered Phrygian scale, dominant ♭2 ♭6 scale (in jazz), Freygish scale, Phrygian harmonic (♮3) scale |
Lydian harmonic (♯2) scale | super Locrian altered diminished scale |
harmonic minor, Aeolian harmonic (♮7) scale |
Locrian harmonic (♮6) scale | Ionian harmonic (♯5) scale, augmented major scale |
| Dorian harmonic (♭5) scale | Dorian harmonic (♭5) scale, Locrian ♮2 ♮6 scale |
altered dominant ♮5 scale, Phrygian harmonic (♭4) scale |
melodic minor ♯4 scale, Lydian harmonic (♭3) scale |
Mixolydian harmonic (♭2) scale | Lydian augmented ♯2 scale | Locrian harmonic ( |
harmonic major, Ionian harmonic (♭6) scale |
Aeolian dominant scale (Dorian ♯3 ♭6 scale) can be called “anti-Dorian scale”, since it and Dorian scale are the only two scales which are self-dual.
- Dual triads
- major triad ~ minor triad
- diminished triad (self-dual)
- augmented triad (self-dual)
- Dual seventh chords
major seventh chord (self-dual) dominant seventh chord ~ half-diminished seventh chord minor seventh chord (self-dual) augmented major seventh chord ~ minor major seventh chord diminished seventh chord (self-dual)
- Dual keys
- D (self-dual)
- A ~ G
- E ~ C
- B ~ F
- F♯ ~ B♭
- C♯ ~ E♭
- G♯ ~ A♭ (self-dual)
- D♯ ~ D♭
- A♯ ~ G♭
- E♯ ~ C♭
- B♯ ~ F♭
Analogues in different musical traditions
- Maqam (Arabic music); Makam (Arabic, Persian and Turkish classical music); Mugham (Azerbaijani music)
- Cantillation (Jewish music)
- Echos (Byzantine music)
- Dastgah (Persian traditional music)
- Raga (Indian classical music)
- Thaat (North Indian or Hindustani music)
- Pann (Ancient Tamil music) > Melakarta (South Indian or Carnatic music)
- Pathet (Javanese music for gamelan)
- Pentatonic scale
See also
References
Footnotes
- ^ Powers (2001), §I,3
- Powers (2001), §V,1
- Powers (2001), §III,1
- Dahlhaus (1968), pp. 174 et passim
- Meier (1974)
- Meier (1992)
- Powers (2001), §1,2
- N. Meeùs, "Modi vocum. Réflections sur la théorie modale médiévale." Con-Scientia Musica. Contrapunti per Rossana Dalmonte e Mario Baroni, A. R. Addessi e. a. ed., Lucca, Libreria Musicale Italiana, 2010, pp. 21-33
- Powers (2001), Introduction
- A. M. Busse Berger, "The Evolution of Rhythmic Notation", The Cambridge History of Western Music Theory, Th. Christensen ed., Cambridge University Press 2002, pp. 628-656, particularly pp. 629-635
- ^ Winnington-Ingram (1936), pp. 2–3
- Porter (2001)
- ^ Mathiesen (2001a), 6(iii)(e)
- Barbera (1984), p. 240
- Mathiesen (2001a), 6(iii)(d)
- Bélis (2001)
- Cleonides (1965), pp. 35–36
- Cleonides (1965), pp. 39–40
- Mathiesen (2001a), 6(iii)(c)
- Palisca (2006), p. 77
- ^ Cleonides (1965), p. 44
- Solomon (1984), pp. 244–245
- West (1992),
- Mathiesen (2001c)
- Mathiesen (2001b)
- ^ Anderson and Mathiesen (2001)
- Barker (1984–89), 2:14–15
- Plato (1902), III.10–III.12 = 398C–403C
- Aristotle (1895), viii:1340a:40–1340b:5
- ^ Barker (1984–89), 1:175–176
- Cleonides (1965), p. 35
- Mathiesen (2001a), 6(iii)
- Mathiesen (1983), i.12
- Mathiesen (2001a), p. 4
- Mathiesen (1983), p. 75
- Nikodēmos ’Agioreitēs (1836), 1:32–33
- Barton (2009)
- ^ Powers (2001), §II.1(ii)
- Powers (2001)
- Palisca (1984), p. 222
- Bower (1984), pp. 253, 260–261
- Powers (2001), §II.1(i)
- Powers (2001), §II.2
- Powers (2001), §II.2(ii)
- Rockstro (1880), p. 343
- Apel (1969), p. 166
- Smith (1989), p. 14
- Fallows (2001)
- Hoppin (1978), p. 67
- ^ Rockstro (1880), p. 342
- Powers (2001), §II.3.i(b), Ex. 5
- ^ Powers (2001), §III.4(ii)(a)
- Powers (2001), §III.4(iii)
- Powers (2001), §III.5(i & ii)
- Curtis (1997), p. 256
- ^ Curtis (1997), p. 255
- ^ Dahlhaus (1990), pp. 191–192
- Levine (1995), Figure 2-4
- Boyden (1994), p. 8
- Kolinski, Mieczyslaw (September 9, 2010). "Mode". Encyclopædia Britannica. Retrieved November 13, 2020.
- Carroll (2002), p. 134
- ^ Marx (1852), p. 336
- Marx (1852), pp. 338, 342, 346
- ^ Serna (2013), p. 35
- Carroll (2002), p. 153
- Voitinskaia, Anastasia (9 December 2018). "The Aural Illusions of the Locrian Mode". Musical U. Retrieved 2022-09-04.
- Samson (1977), p. 148
- Carver (2005), 74n4
- Anon. (1896)
- Chafe (1992), pp. 23, 41, 43, 48
- Glareanus (1965), p. 153
- Hiley (2002), §2(b)
- Pratt (1907), p. 67
- Taylor (1876), p. 419
- Wiering (1995), p. 25
- Jones (1974), p. 33
- Cooper (1995), pp. 9–20
- Gómez, Díaz-Báñez, Gómez, and Mora (2014), pp. 121, 123
- Samson (1977),
- Levine (1995), pp. 55–77
Bibliography
- Anderson, Warren, and Thomas J. Mathiesen (2001). "Ethos". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Anon. (1896). "Plain-song". Chambers's Encyclopaedia: A Dictionary of Universal Knowledge, new edition. Volume 8: Peasant to Roumelia. London and Edinburgh: William & Robert Chambers, Ltd.; Philadelphia: J. B. Lippincott Co.
- Apel, Willi (1969). Harvard Dictionary of Music. Harvard University Press. ISBN 978-0-674-37501-7.
- Aristotle (1895). Aristotle's Politics: A Treatise on Government. translated from the Greek of Aristotle by William Ellis, MA, with an Introduction by Henry Morley. London: George Routledge and Sons, Ltd.
- Barbera, André (1984). "Octave Species". The Journal of Musicology 3, no. 3 (July): 229–241. doi:10.1525/jm.1984.3.3.03a00020 JSTOR 763813 (Subscription access)
- Barker, Andrew (ed.) (1984–89). Greek Musical Writings. 2 vols. Cambridge & New York: Cambridge University Press. ISBN 0-521-23593-6 (v. 1) ISBN 0-521-30220-X (v. 2).
- Barton, Louis W. G. (2009). "§ Influence of Byzantium on Western Chant". The Neume Notation Project: Research in Computer Applications to Medieval Chant.
- Bélis, Annie (2001). "Aristoxenus". Grove Music Online. doi:10.1093/gmo/9781561592630.article.01248 (subscription required).
- Bower, Calvin M. (1984). "The Modes of Boethius". The Journal of Musicology 3, no. 3 (July): 252–263. doi:10.1525/jm.1984.3.3.03a00040 JSTOR 763815 (subscription required).
- Boyden, David D. (1994). "Manual of Counterpoint". Carl Fischer. ISBN 9780825827648.
- Carroll, Nansi (2002). The Walden School Musicianship Course: A Manual for Teachers. Dublin, New Hampshire, and San Francisco: The Walden School.
- Carver, Anthony F. (2005). "Bruckner and the Phrygian Mode". Music & Letters 86, no. 1:74–99. doi:10.1093/ml/gci004
- Chafe, Eric Thomas (1992). Monteverdi’s Tonal Language. New York: Schirmer Books. ISBN 9780028704951.
- Cleonides (1965). "Harmonic Introduction," translated by Oliver Strunk. In Source Readings in Music History, vol. 1 (Antiquity and the Middle Ages), edited by Oliver Strunk, 34–46. New York: W. W. Norton & Co.
- Cooper, Peter (1995). Mel Bay's Complete Irish Fiddle Player. Pacific, Missouri: Mel Bay Publications. ISBN 0-7866-6557-2.
- Cott, Jonathan (1973). Stockhausen: Conversations with the Composer. New York: Simon and Schuster. ISBN 0-671-21495-0.
- Curtis, Liane (1997). "Mode". In Companion to Medieval and Renaissance Music, edited by Tess Knighton and David Fallows, pp. 255-264. Berkeley: University of California Press. ISBN 0-520-21081-6.
- Dahlhaus, Carl (1968). Untersuchungen über die Entstehung der harmonischen Tonalität. Kassel.
- Dahlhaus, Carl (1990). Studies on the Origin of Harmonic Tonality. Princeton, New Jersey: Princeton University Press. ISBN 0-691-09135-8.
- Fallows, David (2001). "Tenor §1". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Glareanus, Henricus (1965). Dodecachordon, Volume 1, translated by Clement Albin Miller. Musicological Studies and Documents 6. : American Institute of Musicology.
- Gómez, Francisco, José Miguel Díaz-Báñez, Emilia Gómez, and Joaquin Mora (2014). "Flamenco Music and Its Computational Study". In Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture, edited by Gary Greenfield, George Hart, and Reza Sarhangi, 119–126. Phoenix, Arizona: Tessellations Publishing. ISBN 978-1-938664-11-3.
- Hiley, David (2002). "Mode". The Oxford Companion to Music, edited by Alison Latham. Oxford and New York: Oxford University Press. ISBN 978-0-19-866212-9.
- Hoppin, Richard (1978). Medieval Music. The Norton Introduction to Music History. New York: Norton. ISBN 0-393-09090-6.
- Jones, George Thaddeus (1974). Music Theory. Barnes & Noble College Outline Series 137. New York: Barnes & Noble Books. ISBN 0-06-467168-2.
- Levine, Mark (1995). The Jazz Theory Book. Petaluma, California: Sher Music Co. ISBN 1-883217-04-0.
- Marx, Adolf Bernhard (1852). The School of Musical Composition, translated from the fourth edition of the original German by August Heinrich Wehrhan. London: Robert Cocks and Co.; Leipzig: Breitkopf and Härtel.
- Mathiesen, Thomas J. (1983). Aristides Quintilianus. On Music. Translated by Thomas J. Mathiesen. New Haven and London: Yale University Press.
- Mathiesen, Thomas J. (2001a). "Greece, §I: Ancient". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Mathiesen, Thomas J. (2001b). "Harmonia (i)". The New Grove Dictionary of Music and Musicians, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Mathiesen, Thomas J. (2001c). "Tonos". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Meier, Bernhard (1974). Die Tonarten der klassischen Vokalpolyphonie: nach den Quellen dargestellt. Utrecht.
- Meier, Bernhard (1992). Alte Tonarten: dargestellt an der Instrumentalmusik des 16. und 17. Jahrhunderts. Kassel:
- Nikodēmos ’Agioreitēs (1836). ’Eortodromion: ētoi ’ermēneia eis tous admatikous kanonas tōn despotikōn kai theomētorikōn ’eortōn, edited by Benediktos Kralidēs. Venice: N. Gluku. Reprinted, Athens: H.I. Spanos, 1961.
- Palisca, Claude V. (1984). "Introductory Notes on the Historiography of the Greek Modes". The Journal of Musicology 3, no. 3 (Summer): 221–228. doi:10.1525/jm.1984.3.3.03a00010 JSTOR 763812 (subscription required).
- Palisca, Claude V. (2006). Music and Ideas in the Sixteenth and Seventeenth Centuries. Studies in the History of Music Theory and Literature 1. Urbana and Chicago: University of Illinois Press. ISBN 9780252031564.
- Plato (1902). The Republic of Plato, 2 vols., edited with critical notes, commentary, and appendices by James Adam. Cambridge: University Press.
- Porter, James (2001). "Mode §IV: Modal Scales and Traditional Music". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Powers, Harold S. (2001). "Mode". The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell. London: Macmillan Publishers.
- Pratt, Waldo Selden (1907). The History of Music: A Handbook and Guide for Students. New York: G. Schirmer.
- Rockstro, W S (1880). "Modes, the Ecclesiastical". A Dictionary of Music and Musicians (A.D. 1450–1880), by Eminent Writers, English and Foreign, vol. 2, edited by George Grove, D. C. L., 340–343. London: Macmillan.
- Samson, Jim (1977). Music in Transition: A Study of Tonal Expansion and Atonality, 1900–1920. Oxford & New York: Oxford University Press. ISBN 0-460-86150-6.
- Serna, Desi (2013). Guitar Theory for Dummies. Hoboken, New Jersey: John Wiley & Sons. ISBN 9781118646939.
- Smith, Charlotte (1989). A Manual of Sixteenth-Century Contrapuntal Style. Newark: University of Delaware Press; London: Associated University Presses. ISBN 978-0-87413-327-1.
- Solomon, Jon (1984). "Towards a History of Tonoi". The Journal of Musicology 3, no. 3 (July): 242–251. doi:10.1525/jm.1984.3.3.03a00030 JSTOR 763814 (subscription required).
- Taylor, John (1876). The Student's Text-book of the Science of Music. London and Liverpool: George Philip and Son.
- Vieru, Anatol (1985). "Modalism – A 'Third World'". Perspectives of New Music 24, no. 1 (Fall–Winter): 62–71.
- West, Martin L. (1992). Ancient Greek Music. Oxford and New York: Oxford University Press ISBN 0-19-814975-1.
- Wiering, Frans (1995). The Language of the Modes: Studies in the History of Polyphonic Modality. Breukelen: Frans Wiering.
- Winnington-Ingram, Reginald Pepys (1936). Mode in Ancient Greek Music. Cambridge Classical Studies. Cambridge: Cambridge University Press. Reprinted, Amsterdam: Hakkert, 1968.
Further reading
- Brent, Jeff, with Schell Barkley (2011). Modalogy: Scales, Modes & Chords: The Primordial Building Blocks of Music. Milwaukee: Hal Leonard Corporation. ISBN 978-1-4584-1397-0
- Chalmers, John H. (1993). Divisions of the Tetrachord / Peri ton tou tetrakhordou katatomon / Sectiones tetrachordi: A Prolegomenon to the Construction of Musical Scales, edited by Larry Polansky and Carter Scholz, foreword by Lou Harrison. Hanover, New Hampshire: Frog Peak Music. ISBN 0-945996-04-7.
- Fellerer, Karl Gustav (1982). "Kirchenmusikalische Reformbestrebungen um 1800". Analecta Musicologica: Veröffentlichungen der Musikgeschichtlichen Abteilung des Deutschen Historischen Instituts in Rom 21:393–408.
- Grout, Donald, Claude V. Palisca, and J. Peter Burkholder (2006). A History of Western Music. New York: W. W. Norton. 7th edition. ISBN 0-393-97991-1.
- Jowett, Benjamin (1937). The Dialogues of Plato, translated by Benjamin Jowett, third edition, 2 vols. New York: Random House. OCLC 2582139
- Jowett, Benjamin (1943). Aristotle's Politics, translated by Benjamin Jowett. New York: Modern Library.
- Judd, Cristle (ed) (1998). Tonal Structures in Early Music: Criticism and Analysis of Early Music, 1st ed. New York: Garland. ISBN 0-8153-2388-3.
- Levine, Mark (1989). The Jazz Piano Book. Petaluma, California: Sher Music Co. ISBN 0-9614701-5-1.
- Lonnendonker, Hans. 1980. "Deutsch-französische Beziehungen in Choralfragen. Ein Beitrag zur Geschichte des gregorianischen Chorals in der zweiten Hälfte des 19. Jahrhunderts". In Ut mens concordet voci: Festschrift Eugène Cardine zum 75. Geburtstag, edited by Johannes Berchmans Göschl, 280–295. St. Ottilien: EOS-Verlag. ISBN 3-88096-100-X
- Mathiesen, Thomas J. (1999). Apollo's Lyre: Greek Music and Music Theory in Antiquity and the Middle Ages. Publications of the Center for the History of Music Theory and Literature 2. Lincoln: University of Nebraska Press. ISBN 0-8032-3079-6.
- McAlpine, Fiona (2004). "Beginnings and Endings: Defining the Mode in a Medieval Chant". Studia Musicologica Academiae Scientiarum Hungaricae 45, nos. 1 & 2 (17th International Congress of the International Musicological Society IMS Study Group Cantus Planus): 165–177.
- Meeùs, Nicolas [fr] (1997). "Mode et système. Conceptions ancienne et moderne de la modalité". Musurgia 4, no. 3:67–80.
- Meeùs, Nicolas (2000). "Fonctions modales et qualités systémiques". Musicae Scientiae, Forum de discussion 1:55–63.
- Meier, Bernhard (1974). Die Tonarten der klassischen Vokalpolyphonie: nach den Quellen dargestellt. Utrecht.
- Meier, Bernhard (1988). The Modes of Classical Vocal Polyphony: Described According to the Sources, translated from the German by Ellen S. Beebe, with revisions by the author. New York: Broude Brothers. ISBN 978-0-8450-7025-3
- Meier, Bernhard (1992). Alte Tonarten: dargestellt an der Instrumentalmusik des 16. und 17. Jahrhunderts. Kassel
- Miller, Ron (1996). Modal Jazz Composition and Harmony, Vol. 1. Rottenburg, Germany: Advance Music. OCLC 43460635
- Ordoulidis, Nikos. (2011). "The Greek Popular Modes". British Postgraduate Musicology 11 (December). (Online journal, accessed 24 December 2011)
- Pfaff, Maurus (1974). "Die Regensburger Kirchenmusikschule und der cantus gregorianus im 19. und 20. Jahrhundert". Gloria Deo-pax hominibus. Festschrift zum hundertjährigen Bestehen der Kirchenmusikschule Regensburg, Schriftenreihe des Allgemeinen Cäcilien-Verbandes für die Länder der Deutschen Sprache 9, edited by Franz Fleckenstein, 221–252. Bonn: Allgemeiner Cäcilien-Verband, 1974.
- Powers, Harold (1998). "From Psalmody to Tonality". In Tonal Structures in Early Music, edited by Cristle Collins Judd, 275–340. Garland Reference Library of the Humanities 1998; Criticism and Analysis of Early Music 1. New York: Garland Publishing. ISBN 0-8153-2388-3.
- Ruff, Anthony, and Raphael Molitor (2008). "Beyond Medici: The Struggle for Progress in Chant". Sacred Music 135, no. 2 (Summer): 26–44.
- Scharnagl, August (1994). "Carl Proske (1794–1861)". In Musica divina: Ausstellung zum 400. Todesjahr von Giovanni Pierluigi Palestrina und Orlando di Lasso und zum 200. Geburtsjahr von Carl Proske. Ausstellung in der Bischöflichen Zentralbibliothek Regensburg, 4. November 1994 bis 3. Februar 1995, Bischöfliches Zentralarchiv und Bischöfliche Zentralbibliothek Regensburg: Kataloge und Schriften, no. 11, edited by Paul Mai, 12–52. Regensburg: Schnell und Steiner, 1994.
- Schnorr, Klemens (2004). "El cambio de la edición oficial del canto gregoriano de la editorial Pustet/Ratisbona a la de Solesmes en la época del Motu proprio". In El Motu proprio de San Pío X y la Música (1903–2003). Barcelona, 2003, edited by Mariano Lambea, introduction by María Rosario Álvarez Martínez and José Sierra Pérez. Revista de musicología 27, no. 1 (June) 197–209.
- Street, Donald (1976). "The Modes of Limited Transposition". The Musical Times 117, no. 1604 (October): 819–823.
- Vieru, Anatol (1980). Cartea modurilor. Bucharest: Editura Muzicală. English edition, as The Book of Modes, translated by Yvonne Petrescu and Magda Morait. Bucharest: Editura Muzicală, 1993.
- Vieru, Anatol (1992). "Generating Modal Sequences (A Remote Approach to Minimal Music)". Perspectives of New Music 30, no. 2 (Summer): 178–200. JSTOR 3090632
- Vincent, John (1974). The Diatonic Modes in Modern Music, revised edition. Hollywood: Curlew Music. OCLC 249898056
- Wellesz, Egon (1954). "Music of the Eastern Churches". The New Oxford History of Music, vol. 2:14–57. Oxford University Press.
- Wiering, Frans (1998). "Internal and External Views of the Modes". In Tonal Structures in Early Music, edited by Cristle Collins Judd, 87–107. Garland Reference Library of the Humanities 1998; Criticism and Analysis of Early Music 1. New York: Garland Publishing. ISBN 0-8153-2388-3.
External links
- All modes mapped out in all positions for 6, 7 and 8 string guitar
- The use of guitar modes in jazz music
- Neume Notation Project Archived 2011-07-16 at the Wayback Machine
- Division of the Tetrachord, John Chalmers
- Greek and Liturgical Modes
- The Ancient Musical Modes: What Were They?, Eric Friedlander MD
- An interactive demonstration of many scales and modes
- The Music of Ancient Greeks, an approach to the original singing of the Homeric epics and early Greek epic and lyrical poetry by Ioannidis Nikolaos
- Ἀριστοξενου ἁρμονικα στοιχεια: The Harmonics of Aristoxenus, edited with translation notes introduction and index of words by Henry S. Macran. Oxford: Clarendon Press, 1902.
- Monzo, Joe. 2004. "The Measurement of Aristoxenus's Divisions of the Tetrachord"
| Modes in Western music | |||||
|---|---|---|---|---|---|
| Gregorian |
| ||||
| Other | |||||
| Diatonic | |||||
| Jazz minor | |||||
| Harmonic minor | |||||
| Harmonic major | |||||
| Double harmonic scale | |||||