Misplaced Pages

Several techniques can be used to move signals in the time-frequency distribution. Similar to computer graphic techniques, signals can be subjected to horizontal shifting, vertical shifting, dilation (scaling), shearing, rotation, and twisting. These techniques can help to save the bandwidth with proper motions apply on the signals. Moreover, filters with proper motion transformation can save the hardware cost without additional filters.

The following examples assume time in the horizontal axis versus frequency in the vertical axis. As a coincident, the following transformations happen to have the motion properties in the time-frequency distribution.

Shifting

Shifting on time axis is like horizontal shifting in time-frequency distribution. On another hand, shifting on the frequency axis would be vertical shifting in time-frequency distribution.

Horizontal shifting

If t₀ is greater than 0, we would be shifting the signal to the right on time axis. (negative would be left)

STFT, Gabor:

${\displaystyle x(t-t_{0})\rightarrow S_{x}(t-t_{0},f)e^{-j2\pi ft_{0}}}$

WDF:

${\displaystyle x(t-t_{0})\rightarrow W_{x}(t-t_{0},f)\,}$

Vertical shifting

If f₀ is greater than 0, we would be shifting the signal to the upward on frequency axis. (negative would be downward)

STFT, Gabor:

${\displaystyle e^{j2\pi f_{0}t}x(t)\rightarrow S_{x}(t,f-f_{0})}$

WDF:

${\displaystyle e^{j2\pi f_{0}t}x(t)\rightarrow W_{x}(t,f-f_{0})}$

This results in an amplitude modulation signal. This sort of shift is also used in a frequency extender. This sort of shift is also used in most bat detectors.

Such an effect is typically implemented using heterodyning

Dilation

Dilation is like doing scaling on one of the axis and area is the same after the process. When a > 1, it's expanding on time axis, and narrowing on frequency axis ;vice versa when a < 1.

STFT, Gabor:

${\displaystyle {\frac {1}{\sqrt {|a|}}}x({\frac {t}{a}})\rightarrow \approx S_{x}({\frac {t}{a}},af)}$

WDF:

${\displaystyle {\frac {1}{\sqrt {|a|}}}x({\frac {t}{a}})\rightarrow W_{x}({\frac {t}{a}},af)}$

When this kind of dilation is applied to audio, it causes a chipmunk effect.

Time stretching

Time stretching is doing scaling only on the time axis, leaving frequencies the same. When ${\displaystyle a<1}$ (the most common case), it's narrowing on the time axis, reducing the area.

STFT, Gabor:

${\displaystyle \approx S_{x}(at,f)}$

WDF:

${\displaystyle \approx W_{x}(at,f)}$

Shearing

Shearing by definition is moving the side of the signal on one direction. Vertical and Horizontal shearing is introduced here.

On Vertical axis only (frequency)

It's shearing on frequency axis, since this only changes the phase.

${\displaystyle x(t)=e^{j\pi at^{2}}y(t)\,}$

STFT, Gabor:

${\displaystyle S_{x}(t,f)\approx S_{y}(t,f-at)\,}$

WDF:

${\displaystyle W_{x}(t,f)=W_{y}(t,f-at)\,}$

On Horizontal axis only (time)

It's shearing on time axis, since this only changes the time.

${\displaystyle x(t)=e^{j\pi {\frac {t^{2}}{a}}}y(t)\,}$

STFT, Gabor:

${\displaystyle S_{x}(t,f)\approx S_{y}(t-af,f)\,}$

WDF:

${\displaystyle W_{x}(t,f)=W_{y}(t-af,f)\,}$

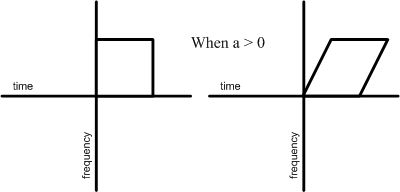
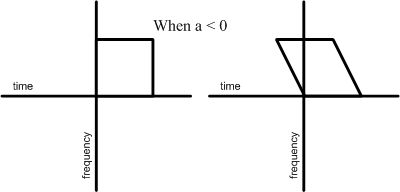
Generalized Shearing

Transforming the time-frequency distribution from a band-like pattern to a curved shape requires the use of polynomials of order three or higher with respect to ${\displaystyle \phi (t)}$. It is beneficial for implementing higher-order modulation, and furthermore, it reduces bandwidth, allowing for lower sampling rates and decreased white noise through filtering.

On Vertical axis only (frequency)

It's shearing on frequency axis, since this only changes the phase.

${\displaystyle x(t)=e^{j\phi (t)}y(t)\,}$

${\displaystyle \phi (t)=\sum \limits _{k=0}^{n}a_{k}t^{k}\,}$

STFT, Gabor:

${\displaystyle S_{x}(t,f)\approx S_{y}(t,f-\sum \limits _{k=1}^{n}{\frac {ka_{k}}{2\pi }}t^{k-1})\,}$

WDF:

${\displaystyle W_{x}(t,f)\approx W_{y}(t,f-\sum \limits _{k=1}^{n}{\frac {ka_{k}}{2\pi }}t^{k-1})\,}$

On Horizontal axis only (time)

It's shearing on time axis, since this only changes the time.

${\displaystyle x(t)=h(t)*y(t)\,}$

${\displaystyle h(t)=IFT(exp(j\sum \limits _{k=0}^{n}a_{k}f^{k}))\,}$

STFT, Gabor:

${\displaystyle S_{x}(t,f)\approx S_{y}(t+\sum \limits _{k=1}^{n}{\frac {ka_{k}}{2\pi }}f^{k-1},f)\,}$

WDF:

${\displaystyle W_{x}(t,f)\approx W_{y}(t+\sum \limits _{k=1}^{n}{\frac {ka_{k}}{2\pi }}f^{k-1},f)\,}$

Rotation

Many transforms has the property of rotations, like Gabor-Wigner, Ambiguity function (counterclockwise), modified Wigner, Cohen's class distribution.

STFT, Gabor, and WDF is introduced in here.

Clockwise rotation by 90 degrees

By switching the time and negative frequency to frequency and time would act like rotating 90 degrees clockwise.

${\displaystyle X(f)=FT(x(t))\,}$

STFT:

${\displaystyle |S_{X}(t,f)|\approx |S_{x}(-f,t)|\,}$

Gabor:

${\displaystyle G_{X}(t,f)=G_{x}(-f,t)e^{-j2\pi ft}\,}$

WDF:

${\displaystyle W_{X}(t,f)=W_{x}(-f,t)\,}$

Counterclockwise rotation by 90 degrees

By switching the negative time and frequency to frequency and time would act like rotating 90 degrees counterclockwise.

If ${\displaystyle X(f)=IFT=\int _{-\infty }^{\infty }x(t)e^{j2\pi ft}\,dt}$, then

${\displaystyle W_{X}(t,f)=W_{x}(f,-t)\,}$

${\displaystyle G_{X}(t,f)=G_{x}(f,-t)e^{j2\pi tf}\,}$

Rotation by 180 degrees

Changing the sign of both time and frequency would be like flipping twice on both axis, and it ends up like doing 180 degrees rotation.

If ${\displaystyle X(f)=x(-t)\,}$, then

${\displaystyle W_{X}(t,f)=W_{x}(-t,-f)\,}$

${\displaystyle G_{X}(t,f)=G_{x}(-t,-f)\,}$

Rotation: Fractional Fourier Transform (FRFTs)

Rotating the time-frequency distribution by the angle other than ${\displaystyle \pi /2,\pi ,3\pi /2}$ and ${\displaystyle 2\pi }$. Compared to Fourier Transform, it transform signal from time domain to fractional domain, domain between time and frequency.

${\displaystyle X_{\phi }(u)={\sqrt {1-jcot\phi }}e^{j\pi cot\phi u^{2}}\int _{-\infty }^{\infty }e^{-j2\pi csc\phi ut}e^{j\pi cot\phi \ t^{2}}x(t)dt,\quad \phi =0.5a\pi }$

For Fourier Transform, ${\displaystyle a=1,\,\phi =0.5\pi }$ and ${\displaystyle csc\phi =1,\,cot\phi =0}$

It is equivalent to the clockwise rotation operation with angle ${\displaystyle \phi }$. for Wigner distribution function and Gabor transform.

Gabor:

${\displaystyle |G_{X_{\phi }}(u,v)|=|G_{x}(ucos\phi -vsin\phi ,usin\phi +vcos\phi )|\,}$

WDF:

${\displaystyle W_{X_{\phi }}(u,v)=W_{x}(ucos\phi -vsin\phi ,usin\phi +vcos\phi )\,}$

Twisting: Linear Canonical Transform (LCT)

The Linear Canonical Transform makes arbitrary linear and integral transformation of a time-frequency distribution.

${\displaystyle F_{(a,b,c,d)}(u)={\sqrt {\frac {1}{jb}}}e^{j\pi {\frac {d}{b}}u^{2}}\int _{-\infty }^{\infty }e^{-j2\pi {\frac {1}{b}}ut}e^{-j\pi {\frac {a}{b}}t^{2}}x(t)dt,\quad b\neq 0}$

${\displaystyle F_{(a,0,c,d)}(u)={\sqrt {d}}e^{j\pi cdu^{2}}x(du),\quad b=0}$

Constraint:

${\displaystyle ab-bc=1}$

Transformation Type

a. fractional Fourier transform

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}={\begin{bmatrix}cos\phi &sin\phi \\-sin\phi &cos\phi \end{bmatrix}}}$

• Fourier transform: ${\displaystyle \phi =\pi /2}$
• identity operation: ${\displaystyle \phi =0}$
• inverse Fourier transform: ${\displaystyle \phi =-\pi /2}$

b. Fresnel transform (convolution with a chirp)

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}={\begin{bmatrix}1&\lambda z\\0&1\end{bmatrix}}}$

c. chirp multiplication

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}={\begin{bmatrix}1&0\\\tau &1\end{bmatrix}}}$

d. scaling

${\displaystyle {\begin{bmatrix}a&b\\c&d\end{bmatrix}}={\begin{bmatrix}{\frac {1}{\sigma }}&0\\0&\sigma \end{bmatrix}}}$

Example

If we want the left image to become the right image, we can use the techniques from above to achieve the requirement.

There are several ways to solve this problem, this is one of the possible solutions.

First, we apply clockwise rotation of 90 degree by using one of the transform.

STFT:

${\displaystyle |S_{X}(t,f)|\approx |S_{x}(-f,t)|\,}$

Gabor:

${\displaystyle G_{X}(t,f)=G_{x}(-f,t)e^{-j2\pi ft}\,}$

WDF:

${\displaystyle W_{X}(t,f)=W_{x}(-f,t)\,}$

Second, we set a = 1/3, and perform a horizontal shearing on t-axis.

STFT, Gabor:

${\displaystyle S_{x}(t,f)\approx S_{y}(t-{\frac {1}{3}}f,f)\,}$

WDF:

${\displaystyle W_{x}(t,f)=W_{y}(t-{\frac {1}{3}}f,f)\,}$

Third, we shift the signal 2 to the right on t-axis by setting t₀ = 2

STFT, Gabor:

${\displaystyle x(t-t_{0})\rightarrow S_{x}(t-2,f)e^{-j2\pi ft_{0}}}$

WDF:

${\displaystyle x(t-t_{0})\rightarrow W_{x}(t-2,f)\,}$

Finally, we shift the signal 1 to the left on f-axis by setting f₀ = -1

STFT, Gabor:

${\displaystyle e^{j2\pi f_{0}t}x(t)\rightarrow S_{x}(t,f+1)}$

WDF:

${\displaystyle e^{j2\pi f_{0}t}x(t)\rightarrow W_{x}(t,f+1)}$

Applications

Efficient Sampling

As mentioned in the introduction, the above techniques can be used to save the bandwidth or the filter cost.

Assume the signal look like this.

.

The dashed box is the filter, and the area of the dashed box would be the bandwidth required.

After some operations like the above example, the signal turn into the position like this.

As a result, the bandwidth was saved, since the area became smaller. Moreover, only a lowpass filter is required to recover the signal, instead of a bandpass filter.

Signal Decomposition and Filter Design

Signal is decomposed into several components and filter removes the undesired component of a signal. The Fourier transform is suitable to filter out the noise that is a combination of sinusoid functions. If signal are not separable in both time and frequency domains, using the fractional Fourier transform (FRFTs) is suitable to filter out the noise that is a combination of higher order exponential functions.

Fiter designed by the fractional Fourier transform:

${\displaystyle x_{o}(t)=O_{F}^{-\phi }{O_{F}^{\phi }H(u)}}$

${\displaystyle O_{F}^{\phi }(x(t))={\sqrt {1-jcot\phi }}e^{j\pi cot\phi u^{2}}\int _{-\infty }^{\infty }e^{-j2\pi csc\phi ut}e^{j\pi cot\phi \ t^{2}}x(t)dt\quad (FRFTs)}$

(1) If ${\displaystyle H(u)=S(-u+u_{0}),\quad H(u)={\begin{cases}1\ \ \ u<u_{0}\\0\ \ \ u>u_{0}\ \ \ \end{cases}}}$

${\displaystyle S(u)}$: Step function

(2) ${\displaystyle \phi }$ is determined by the angle of cutoff line and f-axis.

(3) ${\displaystyle u_{0}}$ equals the distance from origin to cutoff line.

See also

Other time-frequency transforms:

• Short-time Fourier transform
• Wigner distribution function
• Ambiguity function
• Cohen's class distribution function

References

• J.J. Ding, "time-frequency analysis and wavelet transform course note," the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2007.
• J.J. Ding, "time-frequency analysis and wavelet transform homework 3," the Department of Electrical Engineering, National Taiwan University (NTU), Taipei, Taiwan, 2007.

• Integral transforms
• Fourier analysis