Misplaced Pages

Del in cylindrical and spherical coordinates

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Nabla in cylindrical and spherical coordinates) Mathematical gradient operator in certain coordinate systems

This is a list of some vector calculus formulae for working with common curvilinear coordinate systems.

Notes

  • This article uses the standard notation ISO 80000-2, which supersedes ISO 31-11, for spherical coordinates (other sources may reverse the definitions of θ and φ):
    • The polar angle is denoted by θ ∈ [ 0 , π ] {\displaystyle \theta \in } : it is the angle between the z-axis and the radial vector connecting the origin to the point in question.
    • The azimuthal angle is denoted by φ ∈ [ 0 , 2 π ] {\displaystyle \varphi \in } : it is the angle between the x-axis and the projection of the radial vector onto the xy-plane.
  • The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) owing to its domain and image. The classical arctan function has an image of (−π/2, +π/2), whereas atan2 is defined to have an image of (−π, π].

Coordinate conversions

Conversion between Cartesian, cylindrical, and spherical coordinates
From
Cartesian Cylindrical Spherical
To Cartesian x = x y = y z = z {\displaystyle {\begin{aligned}x&=x\\y&=y\\z&=z\\\end{aligned}}} x = ρ cos ⁡ φ y = ρ sin ⁡ φ z = z {\displaystyle {\begin{aligned}x&=\rho \cos \varphi \\y&=\rho \sin \varphi \\z&=z\end{aligned}}} x = r sin ⁡ θ cos ⁡ φ y = r sin ⁡ θ sin ⁡ φ z = r cos ⁡ θ {\displaystyle {\begin{aligned}x&=r\sin \theta \cos \varphi \\y&=r\sin \theta \sin \varphi \\z&=r\cos \theta \\\end{aligned}}}
Cylindrical ρ = x 2 + y 2 φ = arctan ⁡ ( y x ) z = z {\displaystyle {\begin{aligned}\rho &={\sqrt {x^{2}+y^{2}}}\\\varphi &=\arctan \left({\frac {y}{x}}\right)\\z&=z\end{aligned}}} ρ = ρ φ = φ z = z {\displaystyle {\begin{aligned}\rho &=\rho \\\varphi &=\varphi \\z&=z\\\end{aligned}}} ρ = r sin ⁡ θ φ = φ z = r cos ⁡ θ {\displaystyle {\begin{aligned}\rho &=r\sin \theta \\\varphi &=\varphi \\z&=r\cos \theta \end{aligned}}}
Spherical r = x 2 + y 2 + z 2 θ = arctan ⁡ ( x 2 + y 2 z ) φ = arctan ⁡ ( y x ) {\displaystyle {\begin{aligned}r&={\sqrt {x^{2}+y^{2}+z^{2}}}\\\theta &=\arctan \left({\frac {\sqrt {x^{2}+y^{2}}}{z}}\right)\\\varphi &=\arctan \left({\frac {y}{x}}\right)\end{aligned}}} r = ρ 2 + z 2 θ = arctan ⁡ ( ρ z ) φ = φ {\displaystyle {\begin{aligned}r&={\sqrt {\rho ^{2}+z^{2}}}\\\theta &=\arctan {\left({\frac {\rho }{z}}\right)}\\\varphi &=\varphi \end{aligned}}} r = r θ = θ φ = φ {\displaystyle {\begin{aligned}r&=r\\\theta &=\theta \\\varphi &=\varphi \end{aligned}}}

Note that the operation arctan ⁡ ( A B ) {\displaystyle \arctan \left({\frac {A}{B}}\right)} must be interpreted as the two-argument inverse tangent, atan2.

Unit vector conversions

Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of destination coordinates
Cartesian Cylindrical Spherical
Cartesian x ^ = x ^ y ^ = y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} x ^ = cos ⁡ φ ρ ^ − sin ⁡ φ φ ^ y ^ = sin ⁡ φ ρ ^ + cos ⁡ φ φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\cos \varphi {\hat {\boldsymbol {\rho }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \varphi {\hat {\boldsymbol {\rho }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} x ^ = sin ⁡ θ cos ⁡ φ r ^ + cos ⁡ θ cos ⁡ φ θ ^ − sin ⁡ φ φ ^ y ^ = sin ⁡ θ sin ⁡ φ r ^ + cos ⁡ θ sin ⁡ φ θ ^ + cos ⁡ φ φ ^ z ^ = cos ⁡ θ r ^ − sin ⁡ θ θ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&=\sin \theta \cos \varphi {\hat {\mathbf {r} }}+\cos \theta \cos \varphi {\hat {\boldsymbol {\theta }}}-\sin \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {y} }}&=\sin \theta \sin \varphi {\hat {\mathbf {r} }}+\cos \theta \sin \varphi {\hat {\boldsymbol {\theta }}}+\cos \varphi {\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}}
Cylindrical ρ ^ = x x ^ + y y ^ x 2 + y 2 φ ^ = − y x ^ + x y ^ x 2 + y 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} ρ ^ = ρ ^ φ ^ = φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} ρ ^ = sin ⁡ θ r ^ + cos ⁡ θ θ ^ φ ^ = φ ^ z ^ = cos ⁡ θ r ^ − sin ⁡ θ θ ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\sin \theta {\hat {\mathbf {r} }}+\cos \theta {\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&=\cos \theta {\hat {\mathbf {r} }}-\sin \theta {\hat {\boldsymbol {\theta }}}\end{aligned}}}
Spherical r ^ = x x ^ + y y ^ + z z ^ x 2 + y 2 + z 2 θ ^ = ( x x ^ + y y ^ ) z − ( x 2 + y 2 ) z ^ x 2 + y 2 + z 2 x 2 + y 2 φ ^ = − y x ^ + x y ^ x 2 + y 2 {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}+z{\hat {\mathbf {z} }}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {\left(x{\hat {\mathbf {x} }}+y{\hat {\mathbf {y} }}\right)z-\left(x^{2}+y^{2}\right){\hat {\mathbf {z} }}}{{\sqrt {x^{2}+y^{2}+z^{2}}}{\sqrt {x^{2}+y^{2}}}}}\\{\hat {\boldsymbol {\varphi }}}&={\frac {-y{\hat {\mathbf {x} }}+x{\hat {\mathbf {y} }}}{\sqrt {x^{2}+y^{2}}}}\end{aligned}}} r ^ = ρ ρ ^ + z z ^ ρ 2 + z 2 θ ^ = z ρ ^ − ρ z ^ ρ 2 + z 2 φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\frac {\rho {\hat {\boldsymbol {\rho }}}+z{\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\theta }}}&={\frac {z{\hat {\boldsymbol {\rho }}}-\rho {\hat {\mathbf {z} }}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}} r ^ = r ^ θ ^ = θ ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}
Conversion between unit vectors in Cartesian, cylindrical, and spherical coordinate systems in terms of source coordinates
Cartesian Cylindrical Spherical
Cartesian x ^ = x ^ y ^ = y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\hat {\mathbf {x} }}\\{\hat {\mathbf {y} }}&={\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} x ^ = x ρ ^ − y φ ^ x 2 + y 2 y ^ = y ρ ^ + x φ ^ x 2 + y 2 z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x{\hat {\boldsymbol {\rho }}}-y{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {y} }}&={\frac {y{\hat {\boldsymbol {\rho }}}+x{\hat {\boldsymbol {\varphi }}}}{\sqrt {x^{2}+y^{2}}}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} x ^ = x ( x 2 + y 2 r ^ + z θ ^ ) − y x 2 + y 2 + z 2 φ ^ x 2 + y 2 x 2 + y 2 + z 2 y ^ = y ( x 2 + y 2 r ^ + z θ ^ ) + x x 2 + y 2 + z 2 φ ^ x 2 + y 2 x 2 + y 2 + z 2 z ^ = z r ^ − x 2 + y 2 θ ^ x 2 + y 2 + z 2 {\displaystyle {\begin{aligned}{\hat {\mathbf {x} }}&={\frac {x\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)-y{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {y} }}&={\frac {y\left({\sqrt {x^{2}+y^{2}}}{\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}\right)+x{\sqrt {x^{2}+y^{2}+z^{2}}}{\hat {\boldsymbol {\varphi }}}}{{\sqrt {x^{2}+y^{2}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-{\sqrt {x^{2}+y^{2}}}{\hat {\boldsymbol {\theta }}}}{\sqrt {x^{2}+y^{2}+z^{2}}}}\end{aligned}}}
Cylindrical ρ ^ = cos ⁡ φ x ^ + sin ⁡ φ y ^ φ ^ = − sin ⁡ φ x ^ + cos ⁡ φ y ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&=\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\end{aligned}}} ρ ^ = ρ ^ φ ^ = φ ^ z ^ = z ^ {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\hat {\boldsymbol {\rho }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\hat {\mathbf {z} }}\\\end{aligned}}} ρ ^ = ρ r ^ + z θ ^ ρ 2 + z 2 φ ^ = φ ^ z ^ = z r ^ − ρ θ ^ ρ 2 + z 2 {\displaystyle {\begin{aligned}{\hat {\boldsymbol {\rho }}}&={\frac {\rho {\hat {\mathbf {r} }}+z{\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\{\hat {\mathbf {z} }}&={\frac {z{\hat {\mathbf {r} }}-\rho {\hat {\boldsymbol {\theta }}}}{\sqrt {\rho ^{2}+z^{2}}}}\end{aligned}}}
Spherical r ^ = sin ⁡ θ ( cos ⁡ φ x ^ + sin ⁡ φ y ^ ) + cos ⁡ θ z ^ θ ^ = cos ⁡ θ ( cos ⁡ φ x ^ + sin ⁡ φ y ^ ) − sin ⁡ θ z ^ φ ^ = − sin ⁡ φ x ^ + cos ⁡ φ y ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta \left(\cos \varphi {\hat {\mathbf {x} }}+\sin \varphi {\hat {\mathbf {y} }}\right)-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&=-\sin \varphi {\hat {\mathbf {x} }}+\cos \varphi {\hat {\mathbf {y} }}\end{aligned}}} r ^ = sin ⁡ θ ρ ^ + cos ⁡ θ z ^ θ ^ = cos ⁡ θ ρ ^ − sin ⁡ θ z ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&=\sin \theta {\hat {\boldsymbol {\rho }}}+\cos \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\theta }}}&=\cos \theta {\hat {\boldsymbol {\rho }}}-\sin \theta {\hat {\mathbf {z} }}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\end{aligned}}} r ^ = r ^ θ ^ = θ ^ φ ^ = φ ^ {\displaystyle {\begin{aligned}{\hat {\mathbf {r} }}&={\hat {\mathbf {r} }}\\{\hat {\boldsymbol {\theta }}}&={\hat {\boldsymbol {\theta }}}\\{\hat {\boldsymbol {\varphi }}}&={\hat {\boldsymbol {\varphi }}}\\\end{aligned}}}

Del formula

Table with the del operator in cartesian, cylindrical and spherical coordinates
Operation Cartesian coordinates (x, y, z) Cylindrical coordinates (ρ, φ, z) Spherical coordinates (r, θ, φ),
where θ is the polar angle and φ is the azimuthal angle
Vector field A A x x ^ + A y y ^ + A z z ^ {\displaystyle A_{x}{\hat {\mathbf {x} }}+A_{y}{\hat {\mathbf {y} }}+A_{z}{\hat {\mathbf {z} }}} A ρ ρ ^ + A φ φ ^ + A z z ^ {\displaystyle A_{\rho }{\hat {\boldsymbol {\rho }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}+A_{z}{\hat {\mathbf {z} }}} A r r ^ + A θ θ ^ + A φ φ ^ {\displaystyle A_{r}{\hat {\mathbf {r} }}+A_{\theta }{\hat {\boldsymbol {\theta }}}+A_{\varphi }{\hat {\boldsymbol {\varphi }}}}
Gradient ∇f ∂ f ∂ x x ^ + ∂ f ∂ y y ^ + ∂ f ∂ z z ^ {\displaystyle {\partial f \over \partial x}{\hat {\mathbf {x} }}+{\partial f \over \partial y}{\hat {\mathbf {y} }}+{\partial f \over \partial z}{\hat {\mathbf {z} }}} ∂ f ∂ ρ ρ ^ + 1 ρ ∂ f ∂ φ φ ^ + ∂ f ∂ z z ^ {\displaystyle {\partial f \over \partial \rho }{\hat {\boldsymbol {\rho }}}+{1 \over \rho }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}+{\partial f \over \partial z}{\hat {\mathbf {z} }}} ∂ f ∂ r r ^ + 1 r ∂ f ∂ θ θ ^ + 1 r sin ⁡ θ ∂ f ∂ φ φ ^ {\displaystyle {\partial f \over \partial r}{\hat {\mathbf {r} }}+{1 \over r}{\partial f \over \partial \theta }{\hat {\boldsymbol {\theta }}}+{1 \over r\sin \theta }{\partial f \over \partial \varphi }{\hat {\boldsymbol {\varphi }}}}
Divergence ∇ ⋅ A ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\partial A_{x} \over \partial x}+{\partial A_{y} \over \partial y}+{\partial A_{z} \over \partial z}} 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A φ ∂ φ + ∂ A z ∂ z {\displaystyle {1 \over \rho }{\partial \left(\rho A_{\rho }\right) \over \partial \rho }+{1 \over \rho }{\partial A_{\varphi } \over \partial \varphi }+{\partial A_{z} \over \partial z}} 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin ⁡ θ ∂ ∂ θ ( A θ sin ⁡ θ ) + 1 r sin ⁡ θ ∂ A φ ∂ φ {\displaystyle {1 \over r^{2}}{\partial \left(r^{2}A_{r}\right) \over \partial r}+{1 \over r\sin \theta }{\partial \over \partial \theta }\left(A_{\theta }\sin \theta \right)+{1 \over r\sin \theta }{\partial A_{\varphi } \over \partial \varphi }}
Curl ∇ × A ( ∂ A z ∂ y − ∂ A y ∂ z ) x ^ + ( ∂ A x ∂ z − ∂ A z ∂ x ) y ^ + ( ∂ A y ∂ x − ∂ A x ∂ y ) z ^ {\displaystyle {\begin{aligned}\left({\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial A_{x}}{\partial z}}-{\frac {\partial A_{z}}{\partial x}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial A_{y}}{\partial x}}-{\frac {\partial A_{x}}{\partial y}}\right)&{\hat {\mathbf {z} }}\end{aligned}}} ( 1 ρ ∂ A z ∂ φ − ∂ A φ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) φ ^ + 1 ρ ( ∂ ( ρ A φ ) ∂ ρ − ∂ A ρ ∂ φ ) z ^ {\displaystyle {\begin{aligned}\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}-{\frac {\partial A_{\varphi }}{\partial z}}\right)&{\hat {\boldsymbol {\rho }}}\\+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+{\frac {1}{\rho }}\left({\frac {\partial \left(\rho A_{\varphi }\right)}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \varphi }}\right)&{\hat {\mathbf {z} }}\end{aligned}}} 1 r sin ⁡ θ ( ∂ ∂ θ ( A φ sin ⁡ θ ) − ∂ A θ ∂ φ ) r ^ + 1 r ( 1 sin ⁡ θ ∂ A r ∂ φ − ∂ ∂ r ( r A φ ) ) θ ^ + 1 r ( ∂ ∂ r ( r A θ ) − ∂ A r ∂ θ ) φ ^ {\displaystyle {\begin{aligned}{\frac {1}{r\sin \theta }}\left({\frac {\partial }{\partial \theta }}\left(A_{\varphi }\sin \theta \right)-{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\{}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {\partial }{\partial r}}\left(rA_{\varphi }\right)\right)&{\hat {\boldsymbol {\theta }}}\\{}+{\frac {1}{r}}\left({\frac {\partial }{\partial r}}\left(rA_{\theta }\right)-{\frac {\partial A_{r}}{\partial \theta }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Laplace operator ∇f ≡ ∆f ∂ 2 f ∂ x 2 + ∂ 2 f ∂ y 2 + ∂ 2 f ∂ z 2 {\displaystyle {\partial ^{2}f \over \partial x^{2}}+{\partial ^{2}f \over \partial y^{2}}+{\partial ^{2}f \over \partial z^{2}}} 1 ρ ∂ ∂ ρ ( ρ ∂ f ∂ ρ ) + 1 ρ 2 ∂ 2 f ∂ φ 2 + ∂ 2 f ∂ z 2 {\displaystyle {1 \over \rho }{\partial \over \partial \rho }\left(\rho {\partial f \over \partial \rho }\right)+{1 \over \rho ^{2}}{\partial ^{2}f \over \partial \varphi ^{2}}+{\partial ^{2}f \over \partial z^{2}}} 1 r 2 ∂ ∂ r ( r 2 ∂ f ∂ r ) + 1 r 2 sin ⁡ θ ∂ ∂ θ ( sin ⁡ θ ∂ f ∂ θ ) + 1 r 2 sin 2 ⁡ θ ∂ 2 f ∂ φ 2 {\displaystyle {1 \over r^{2}}{\partial \over \partial r}\!\left(r^{2}{\partial f \over \partial r}\right)\!+\!{1 \over r^{2}\!\sin \theta }{\partial \over \partial \theta }\!\left(\sin \theta {\partial f \over \partial \theta }\right)\!+\!{1 \over r^{2}\!\sin ^{2}\theta }{\partial ^{2}f \over \partial \varphi ^{2}}}
Vector gradient ∇A ∂ A x ∂ x x ^ ⊗ x ^ + ∂ A x ∂ y x ^ ⊗ y ^ + ∂ A x ∂ z x ^ ⊗ z ^ + ∂ A y ∂ x y ^ ⊗ x ^ + ∂ A y ∂ y y ^ ⊗ y ^ + ∂ A y ∂ z y ^ ⊗ z ^ + ∂ A z ∂ x z ^ ⊗ x ^ + ∂ A z ∂ y z ^ ⊗ y ^ + ∂ A z ∂ z z ^ ⊗ z ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{x}}{\partial x}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{x}}{\partial y}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{x}}{\partial z}}{\hat {\mathbf {x} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{y}}{\partial x}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{y}}{\partial y}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{y}}{\partial z}}{\hat {\mathbf {y} }}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial x}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {x} }}+{\frac {\partial A_{z}}{\partial y}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {y} }}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}} ∂ A ρ ∂ ρ ρ ^ ⊗ ρ ^ + ( 1 ρ ∂ A ρ ∂ φ − A φ ρ ) ρ ^ ⊗ φ ^ + ∂ A ρ ∂ z ρ ^ ⊗ z ^ + ∂ A φ ∂ ρ φ ^ ⊗ ρ ^ + ( 1 ρ ∂ A φ ∂ φ + A ρ ρ ) φ ^ ⊗ φ ^ + ∂ A φ ∂ z φ ^ ⊗ z ^ + ∂ A z ∂ ρ z ^ ⊗ ρ ^ + 1 ρ ∂ A z ∂ φ z ^ ⊗ φ ^ + ∂ A z ∂ z z ^ ⊗ z ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{\rho }}{\partial \rho }}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \varphi }}-{\frac {A_{\varphi }}{\rho }}\right){\hat {\boldsymbol {\rho }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\rho }}{\partial z}}{\hat {\boldsymbol {\rho }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{\varphi }}{\partial \rho }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\rho }}}+\left({\frac {1}{\rho }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+{\frac {A_{\rho }}{\rho }}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{\varphi }}{\partial z}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {z} }}\\{}+&{\frac {\partial A_{z}}{\partial \rho }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\rho }}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \varphi }}{\hat {\mathbf {z} }}\otimes {\hat {\boldsymbol {\varphi }}}+{\frac {\partial A_{z}}{\partial z}}{\hat {\mathbf {z} }}\otimes {\hat {\mathbf {z} }}\end{aligned}}} ∂ A r ∂ r r ^ ⊗ r ^ + ( 1 r ∂ A r ∂ θ − A θ r ) r ^ ⊗ θ ^ + ( 1 r sin ⁡ θ ∂ A r ∂ φ − A φ r ) r ^ ⊗ φ ^ + ∂ A θ ∂ r θ ^ ⊗ r ^ + ( 1 r ∂ A θ ∂ θ + A r r ) θ ^ ⊗ θ ^ + ( 1 r sin ⁡ θ ∂ A θ ∂ φ − cot ⁡ θ A φ r ) θ ^ ⊗ φ ^ + ∂ A φ ∂ r φ ^ ⊗ r ^ + 1 r ∂ A φ ∂ θ φ ^ ⊗ θ ^ + ( 1 r sin ⁡ θ ∂ A φ ∂ φ + cot ⁡ θ A θ r + A r r ) φ ^ ⊗ φ ^ {\displaystyle {\begin{aligned}{}&{\frac {\partial A_{r}}{\partial r}}{\hat {\mathbf {r} }}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {A_{\theta }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}-{\frac {A_{\varphi }}{r}}\right){\hat {\mathbf {r} }}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\theta }}{\partial r}}{\hat {\boldsymbol {\theta }}}\otimes {\hat {\mathbf {r} }}+\left({\frac {1}{r}}{\frac {\partial A_{\theta }}{\partial \theta }}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}-\cot \theta {\frac {A_{\varphi }}{r}}\right){\hat {\boldsymbol {\theta }}}\otimes {\hat {\boldsymbol {\varphi }}}\\{}+&{\frac {\partial A_{\varphi }}{\partial r}}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\mathbf {r} }}+{\frac {1}{r}}{\frac {\partial A_{\varphi }}{\partial \theta }}{\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\theta }}}+\left({\frac {1}{r\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}+\cot \theta {\frac {A_{\theta }}{r}}+{\frac {A_{r}}{r}}\right){\hat {\boldsymbol {\varphi }}}\otimes {\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Vector Laplacian ∇A ≡ ∆A ∇ 2 A x x ^ + ∇ 2 A y y ^ + ∇ 2 A z z ^ {\displaystyle \nabla ^{2}A_{x}{\hat {\mathbf {x} }}+\nabla ^{2}A_{y}{\hat {\mathbf {y} }}+\nabla ^{2}A_{z}{\hat {\mathbf {z} }}}

( ∇ 2 A ρ − A ρ ρ 2 − 2 ρ 2 ∂ A φ ∂ φ ) ρ ^ + ( ∇ 2 A φ − A φ ρ 2 + 2 ρ 2 ∂ A ρ ∂ φ ) φ ^ + ∇ 2 A z z ^ {\displaystyle {\begin{aligned}{\mathopen {}}\left(\nabla ^{2}A_{\rho }-{\frac {A_{\rho }}{\rho ^{2}}}-{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\rho }}}\\+{\mathopen {}}\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{\rho ^{2}}}+{\frac {2}{\rho ^{2}}}{\frac {\partial A_{\rho }}{\partial \varphi }}\right){\mathclose {}}&{\hat {\boldsymbol {\varphi }}}\\{}+\nabla ^{2}A_{z}&{\hat {\mathbf {z} }}\end{aligned}}}

( ∇ 2 A r − 2 A r r 2 − 2 r 2 sin ⁡ θ ∂ ( A θ sin ⁡ θ ) ∂ θ − 2 r 2 sin ⁡ θ ∂ A φ ∂ φ ) r ^ + ( ∇ 2 A θ − A θ r 2 sin 2 ⁡ θ + 2 r 2 ∂ A r ∂ θ − 2 cos ⁡ θ r 2 sin 2 ⁡ θ ∂ A φ ∂ φ ) θ ^ + ( ∇ 2 A φ − A φ r 2 sin 2 ⁡ θ + 2 r 2 sin ⁡ θ ∂ A r ∂ φ + 2 cos ⁡ θ r 2 sin 2 ⁡ θ ∂ A θ ∂ φ ) φ ^ {\displaystyle {\begin{aligned}\left(\nabla ^{2}A_{r}-{\frac {2A_{r}}{r^{2}}}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial \left(A_{\theta }\sin \theta \right)}{\partial \theta }}-{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\mathbf {r} }}\\+\left(\nabla ^{2}A_{\theta }-{\frac {A_{\theta }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}}}{\frac {\partial A_{r}}{\partial \theta }}-{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\varphi }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(\nabla ^{2}A_{\varphi }-{\frac {A_{\varphi }}{r^{2}\sin ^{2}\theta }}+{\frac {2}{r^{2}\sin \theta }}{\frac {\partial A_{r}}{\partial \varphi }}+{\frac {2\cos \theta }{r^{2}\sin ^{2}\theta }}{\frac {\partial A_{\theta }}{\partial \varphi }}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}

Directional derivative (A ⋅ ∇)B A ⋅ ∇ B x x ^ + A ⋅ ∇ B y y ^ + A ⋅ ∇ B z z ^ {\displaystyle \mathbf {A} \cdot \nabla B_{x}{\hat {\mathbf {x} }}+\mathbf {A} \cdot \nabla B_{y}{\hat {\mathbf {y} }}+\mathbf {A} \cdot \nabla B_{z}{\hat {\mathbf {z} }}} ( A ρ ∂ B ρ ∂ ρ + A φ ρ ∂ B ρ ∂ φ + A z ∂ B ρ ∂ z − A φ B φ ρ ) ρ ^ + ( A ρ ∂ B φ ∂ ρ + A φ ρ ∂ B φ ∂ φ + A z ∂ B φ ∂ z + A φ B ρ ρ ) φ ^ + ( A ρ ∂ B z ∂ ρ + A φ ρ ∂ B z ∂ φ + A z ∂ B z ∂ z ) z ^ {\displaystyle {\begin{aligned}\left(A_{\rho }{\frac {\partial B_{\rho }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\rho }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\rho }}{\partial z}}-{\frac {A_{\varphi }B_{\varphi }}{\rho }}\right)&{\hat {\boldsymbol {\rho }}}\\+\left(A_{\rho }{\frac {\partial B_{\varphi }}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+A_{z}{\frac {\partial B_{\varphi }}{\partial z}}+{\frac {A_{\varphi }B_{\rho }}{\rho }}\right)&{\hat {\boldsymbol {\varphi }}}\\+\left(A_{\rho }{\frac {\partial B_{z}}{\partial \rho }}+{\frac {A_{\varphi }}{\rho }}{\frac {\partial B_{z}}{\partial \varphi }}+A_{z}{\frac {\partial B_{z}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}

( A r ∂ B r ∂ r + A θ r ∂ B r ∂ θ + A φ r sin ⁡ θ ∂ B r ∂ φ − A θ B θ + A φ B φ r ) r ^ + ( A r ∂ B θ ∂ r + A θ r ∂ B θ ∂ θ + A φ r sin ⁡ θ ∂ B θ ∂ φ + A θ B r r − A φ B φ cot ⁡ θ r ) θ ^ + ( A r ∂ B φ ∂ r + A θ r ∂ B φ ∂ θ + A φ r sin ⁡ θ ∂ B φ ∂ φ + A φ B r r + A φ B θ cot ⁡ θ r ) φ ^ {\displaystyle {\begin{aligned}\left(A_{r}{\frac {\partial B_{r}}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{r}}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{r}}{\partial \varphi }}-{\frac {A_{\theta }B_{\theta }+A_{\varphi }B_{\varphi }}{r}}\right)&{\hat {\mathbf {r} }}\\+\left(A_{r}{\frac {\partial B_{\theta }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\theta }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\theta }}{\partial \varphi }}+{\frac {A_{\theta }B_{r}}{r}}-{\frac {A_{\varphi }B_{\varphi }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\theta }}}\\+\left(A_{r}{\frac {\partial B_{\varphi }}{\partial r}}+{\frac {A_{\theta }}{r}}{\frac {\partial B_{\varphi }}{\partial \theta }}+{\frac {A_{\varphi }}{r\sin \theta }}{\frac {\partial B_{\varphi }}{\partial \varphi }}+{\frac {A_{\varphi }B_{r}}{r}}+{\frac {A_{\varphi }B_{\theta }\cot \theta }{r}}\right)&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}

Tensor divergence ∇ ⋅ T

( ∂ T x x ∂ x + ∂ T y x ∂ y + ∂ T z x ∂ z ) x ^ + ( ∂ T x y ∂ x + ∂ T y y ∂ y + ∂ T z y ∂ z ) y ^ + ( ∂ T x z ∂ x + ∂ T y z ∂ y + ∂ T z z ∂ z ) z ^ {\displaystyle {\begin{aligned}\left({\frac {\partial T_{xx}}{\partial x}}+{\frac {\partial T_{yx}}{\partial y}}+{\frac {\partial T_{zx}}{\partial z}}\right)&{\hat {\mathbf {x} }}\\+\left({\frac {\partial T_{xy}}{\partial x}}+{\frac {\partial T_{yy}}{\partial y}}+{\frac {\partial T_{zy}}{\partial z}}\right)&{\hat {\mathbf {y} }}\\+\left({\frac {\partial T_{xz}}{\partial x}}+{\frac {\partial T_{yz}}{\partial y}}+{\frac {\partial T_{zz}}{\partial z}}\right)&{\hat {\mathbf {z} }}\end{aligned}}}

[ ∂ T ρ ρ ∂ ρ + 1 ρ ∂ T φ ρ ∂ φ + ∂ T z ρ ∂ z + 1 ρ ( T ρ ρ − T φ φ ) ] ρ ^ + [ ∂ T ρ φ ∂ ρ + 1 ρ ∂ T φ φ ∂ φ + ∂ T z φ ∂ z + 1 ρ ( T ρ φ + T φ ρ ) ] φ ^ + [ ∂ T ρ z ∂ ρ + 1 ρ ∂ T φ z ∂ φ + ∂ T z z ∂ z + T ρ z ρ ] z ^ {\displaystyle {\begin{aligned}\left&{\hat {\boldsymbol {\rho }}}\\+\left&{\hat {\boldsymbol {\varphi }}}\\+\left&{\hat {\mathbf {z} }}\end{aligned}}}

[ ∂ T r r ∂ r + 2 T r r r + 1 r ∂ T θ r ∂ θ + cot ⁡ θ r T θ r + 1 r sin ⁡ θ ∂ T φ r ∂ φ − 1 r ( T θ θ + T φ φ ) ] r ^ + [ ∂ T r θ ∂ r + 2 T r θ r + 1 r ∂ T θ θ ∂ θ + cot ⁡ θ r T θ θ + 1 r sin ⁡ θ ∂ T φ θ ∂ φ + T θ r r − cot ⁡ θ r T φ φ ] θ ^ + [ ∂ T r φ ∂ r + 2 T r φ r + 1 r ∂ T θ φ ∂ θ + 1 r sin ⁡ θ ∂ T φ φ ∂ φ + T φ r r + cot ⁡ θ r ( T θ φ + T φ θ ) ] φ ^ {\displaystyle {\begin{aligned}\left&{\hat {\mathbf {r} }}\\+\left&{\hat {\boldsymbol {\theta }}}\\+\left&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}

Differential displacement dℓ d x x ^ + d y y ^ + d z z ^ {\displaystyle dx\,{\hat {\mathbf {x} }}+dy\,{\hat {\mathbf {y} }}+dz\,{\hat {\mathbf {z} }}} d ρ ρ ^ + ρ d φ φ ^ + d z z ^ {\displaystyle d\rho \,{\hat {\boldsymbol {\rho }}}+\rho \,d\varphi \,{\hat {\boldsymbol {\varphi }}}+dz\,{\hat {\mathbf {z} }}} d r r ^ + r d θ θ ^ + r sin ⁡ θ d φ φ ^ {\displaystyle dr\,{\hat {\mathbf {r} }}+r\,d\theta \,{\hat {\boldsymbol {\theta }}}+r\,\sin \theta \,d\varphi \,{\hat {\boldsymbol {\varphi }}}}
Differential normal area dS d y d z x ^ + d x d z y ^ + d x d y z ^ {\displaystyle {\begin{aligned}dy\,dz&\,{\hat {\mathbf {x} }}\\{}+dx\,dz&\,{\hat {\mathbf {y} }}\\{}+dx\,dy&\,{\hat {\mathbf {z} }}\end{aligned}}} ρ d φ d z ρ ^ + d ρ d z φ ^ + ρ d ρ d φ z ^ {\displaystyle {\begin{aligned}\rho \,d\varphi \,dz&\,{\hat {\boldsymbol {\rho }}}\\{}+d\rho \,dz&\,{\hat {\boldsymbol {\varphi }}}\\{}+\rho \,d\rho \,d\varphi &\,{\hat {\mathbf {z} }}\end{aligned}}} r 2 sin ⁡ θ d θ d φ r ^ + r sin ⁡ θ d r d φ θ ^ + r d r d θ φ ^ {\displaystyle {\begin{aligned}r^{2}\sin \theta \,d\theta \,d\varphi &\,{\hat {\mathbf {r} }}\\{}+r\sin \theta \,dr\,d\varphi &\,{\hat {\boldsymbol {\theta }}}\\{}+r\,dr\,d\theta &\,{\hat {\boldsymbol {\varphi }}}\end{aligned}}}
Differential volume dV d x d y d z {\displaystyle dx\,dy\,dz} ρ d ρ d φ d z {\displaystyle \rho \,d\rho \,d\varphi \,dz} r 2 sin ⁡ θ d r d θ d φ {\displaystyle r^{2}\sin \theta \,dr\,d\theta \,d\varphi }
^α This page uses θ {\displaystyle \theta } for the polar angle and φ {\displaystyle \varphi } for the azimuthal angle, which is common notation in physics. The source that is used for these formulae uses θ {\displaystyle \theta } for the azimuthal angle and φ {\displaystyle \varphi } for the polar angle, which is common mathematical notation. In order to get the mathematics formulae, switch θ {\displaystyle \theta } and φ {\displaystyle \varphi } in the formulae shown in the table above.
^β Defined in Cartesian coordinates as ∂ i A ⊗ e i {\displaystyle \partial _{i}\mathbf {A} \otimes \mathbf {e} _{i}} . An alternative definition is e i ⊗ ∂ i A {\displaystyle \mathbf {e} _{i}\otimes \partial _{i}\mathbf {A} } .
^γ Defined in Cartesian coordinates as e i ⋅ ∂ i T {\displaystyle \mathbf {e} _{i}\cdot \partial _{i}\mathbf {T} } . An alternative definition is ∂ i T ⋅ e i {\displaystyle \partial _{i}\mathbf {T} \cdot \mathbf {e} _{i}} .

Calculation rules

  1. div grad ⁡ f ≡ ∇ ⋅ ∇ f ≡ ∇ 2 f {\displaystyle \operatorname {div} \,\operatorname {grad} f\equiv \nabla \cdot \nabla f\equiv \nabla ^{2}f}
  2. curl grad ⁡ f ≡ ∇ × ∇ f = 0 {\displaystyle \operatorname {curl} \,\operatorname {grad} f\equiv \nabla \times \nabla f=\mathbf {0} }
  3. div curl ⁡ A ≡ ∇ ⋅ ( ∇ × A ) = 0 {\displaystyle \operatorname {div} \,\operatorname {curl} \mathbf {A} \equiv \nabla \cdot (\nabla \times \mathbf {A} )=0}
  4. curl curl ⁡ A ≡ ∇ × ( ∇ × A ) = ∇ ( ∇ ⋅ A ) − ∇ 2 A {\displaystyle \operatorname {curl} \,\operatorname {curl} \mathbf {A} \equiv \nabla \times (\nabla \times \mathbf {A} )=\nabla (\nabla \cdot \mathbf {A} )-\nabla ^{2}\mathbf {A} } (Lagrange's formula for del)
  5. ∇ 2 ( f g ) = f ∇ 2 g + 2 ∇ f ⋅ ∇ g + g ∇ 2 f {\displaystyle \nabla ^{2}(fg)=f\nabla ^{2}g+2\nabla f\cdot \nabla g+g\nabla ^{2}f}
  6. ∇ 2 ( P ⋅ Q ) = Q ⋅ ∇ 2 P − P ⋅ ∇ 2 Q + 2 ∇ ⋅ [ ( P ⋅ ∇ ) Q + P × ∇ × Q ] {\displaystyle \nabla ^{2}\left(\mathbf {P} \cdot \mathbf {Q} \right)=\mathbf {Q} \cdot \nabla ^{2}\mathbf {P} -\mathbf {P} \cdot \nabla ^{2}\mathbf {Q} +2\nabla \cdot \left\quad } (From )

Cartesian derivation

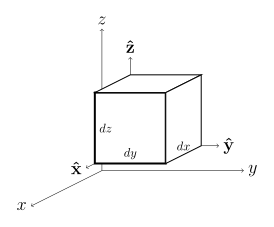
div ⁡ A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A x ( x + d x ) d y d z − A x ( x ) d y d z + A y ( y + d y ) d x d z − A y ( y ) d x d z + A z ( z + d z ) d x d y − A z ( z ) d x d y d x d y d z = ∂ A x ∂ x + ∂ A y ∂ y + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} =\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}&={\frac {A_{x}(x+dx)\,dy\,dz-A_{x}(x)\,dy\,dz+A_{y}(y+dy)\,dx\,dz-A_{y}(y)\,dx\,dz+A_{z}(z+dz)\,dx\,dy-A_{z}(z)\,dx\,dy}{dx\,dy\,dz}}\\&={\frac {\partial A_{x}}{\partial x}}+{\frac {\partial A_{y}}{\partial y}}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}

( curl ⁡ A ) x = lim S ⊥ x ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( y + d y ) d z − A z ( y ) d z + A y ( z ) d y − A y ( z + d z ) d y d y d z = ∂ A z ∂ y − ∂ A y ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{x}=\lim _{S^{\perp \mathbf {\hat {x}} }\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{z}(y+dy)\,dz-A_{z}(y)\,dz+A_{y}(z)\,dy-A_{y}(z+dz)\,dy}{dy\,dz}}\\&={\frac {\partial A_{z}}{\partial y}}-{\frac {\partial A_{y}}{\partial z}}\end{aligned}}}

The expressions for ( curl ⁡ A ) y {\displaystyle (\operatorname {curl} \mathbf {A} )_{y}} and ( curl ⁡ A ) z {\displaystyle (\operatorname {curl} \mathbf {A} )_{z}} are found in the same way.

Cylindrical derivation

div ⁡ A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A ρ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ d z − A ρ ( ρ ) ρ d ϕ d z + A ϕ ( ϕ + d ϕ ) d ρ d z − A ϕ ( ϕ ) d ρ d z + A z ( z + d z ) d ρ ( ρ + d ρ / 2 ) d ϕ − A z ( z ) d ρ ( ρ + d ρ / 2 ) d ϕ ρ d ϕ d ρ d z = 1 ρ ∂ ( ρ A ρ ) ∂ ρ + 1 ρ ∂ A ϕ ∂ ϕ + ∂ A z ∂ z {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{\rho }(\rho +d\rho )(\rho +d\rho )\,d\phi \,dz-A_{\rho }(\rho )\rho \,d\phi \,dz+A_{\phi }(\phi +d\phi )\,d\rho \,dz-A_{\phi }(\phi )\,d\rho \,dz+A_{z}(z+dz)\,d\rho \,(\rho +d\rho /2)\,d\phi -A_{z}(z)\,d\rho (\rho +d\rho /2)\,d\phi }{\rho \,d\phi \,d\rho \,dz}}\\&={\frac {1}{\rho }}{\frac {\partial (\rho A_{\rho })}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial A_{\phi }}{\partial \phi }}+{\frac {\partial A_{z}}{\partial z}}\end{aligned}}}

( curl ⁡ A ) ρ = lim S ⊥ ρ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( z ) ( ρ + d ρ ) d ϕ − A ϕ ( z + d z ) ( ρ + d ρ ) d ϕ + A z ( ϕ + d ϕ ) d z − A z ( ϕ ) d z ( ρ + d ρ ) d ϕ d z = − ∂ A ϕ ∂ z + 1 ρ ∂ A z ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\rho }&=\lim _{S^{\perp {\hat {\boldsymbol {\rho }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\&={\frac {A_{\phi }(z)\left(\rho +d\rho \right)\,d\phi -A_{\phi }(z+dz)\left(\rho +d\rho \right)\,d\phi +A_{z}(\phi +d\phi )\,dz-A_{z}(\phi )\,dz}{\left(\rho +d\rho \right)\,d\phi \,dz}}\\&=-{\frac {\partial A_{\phi }}{\partial z}}+{\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}\end{aligned}}}

( curl ⁡ A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A z ( ρ ) d z − A z ( ρ + d ρ ) d z + A ρ ( z + d z ) d ρ − A ρ ( z ) d ρ d ρ d z = − ∂ A z ∂ ρ + ∂ A ρ ∂ z {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }&=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}}{\iint _{S}dS}}\\&={\frac {A_{z}(\rho )\,dz-A_{z}(\rho +d\rho )\,dz+A_{\rho }(z+dz)\,d\rho -A_{\rho }(z)\,d\rho }{d\rho \,dz}}\\&=-{\frac {\partial A_{z}}{\partial \rho }}+{\frac {\partial A_{\rho }}{\partial z}}\end{aligned}}}

( curl ⁡ A ) z = lim S ⊥ z ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ρ ( ϕ ) d ρ − A ρ ( ϕ + d ϕ ) d ρ + A ϕ ( ρ + d ρ ) ( ρ + d ρ ) d ϕ − A ϕ ( ρ ) ρ d ϕ ρ d ρ d ϕ = − 1 ρ ∂ A ρ ∂ ϕ + 1 ρ ∂ ( ρ A ϕ ) ∂ ρ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{z}&=\lim _{S^{\perp {\hat {\boldsymbol {z}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}\\&={\frac {A_{\rho }(\phi )\,d\rho -A_{\rho }(\phi +d\phi )\,d\rho +A_{\phi }(\rho +d\rho )(\rho +d\rho )\,d\phi -A_{\phi }(\rho )\rho \,d\phi }{\rho \,d\rho \,d\phi }}\\&=-{\frac {1}{\rho }}{\frac {\partial A_{\rho }}{\partial \phi }}+{\frac {1}{\rho }}{\frac {\partial (\rho A_{\phi })}{\partial \rho }}\end{aligned}}}

curl ⁡ A = ( curl ⁡ A ) ρ ρ ^ + ( curl ⁡ A ) ϕ ϕ ^ + ( curl ⁡ A ) z z ^ = ( 1 ρ ∂ A z ∂ ϕ − ∂ A ϕ ∂ z ) ρ ^ + ( ∂ A ρ ∂ z − ∂ A z ∂ ρ ) ϕ ^ + 1 ρ ( ∂ ( ρ A ϕ ) ∂ ρ − ∂ A ρ ∂ ϕ ) z ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{\rho }{\hat {\boldsymbol {\rho }}}+(\operatorname {curl} \mathbf {A} )_{\phi }{\hat {\boldsymbol {\phi }}}+(\operatorname {curl} \mathbf {A} )_{z}{\hat {\boldsymbol {z}}}\\&=\left({\frac {1}{\rho }}{\frac {\partial A_{z}}{\partial \phi }}-{\frac {\partial A_{\phi }}{\partial z}}\right){\hat {\boldsymbol {\rho }}}+\left({\frac {\partial A_{\rho }}{\partial z}}-{\frac {\partial A_{z}}{\partial \rho }}\right){\hat {\boldsymbol {\phi }}}+{\frac {1}{\rho }}\left({\frac {\partial (\rho A_{\phi })}{\partial \rho }}-{\frac {\partial A_{\rho }}{\partial \phi }}\right){\hat {\boldsymbol {z}}}\end{aligned}}}

Spherical derivation

div ⁡ A = lim V → 0 ∬ ∂ V A ⋅ d S ∭ V d V = A r ( r + d r ) ( r + d r ) d θ ( r + d r ) sin ⁡ θ d ϕ − A r ( r ) r d θ r sin ⁡ θ d ϕ + A θ ( θ + d θ ) sin ⁡ ( θ + d θ ) r d r d ϕ − A θ ( θ ) sin ⁡ ( θ ) r d r d ϕ + A ϕ ( ϕ + d ϕ ) r d r d θ − A ϕ ( ϕ ) r d r d θ d r r d θ r sin ⁡ θ d ϕ = 1 r 2 ∂ ( r 2 A r ) ∂ r + 1 r sin ⁡ θ ∂ ( A θ sin ⁡ θ ) ∂ θ + 1 r sin ⁡ θ ∂ A ϕ ∂ ϕ {\displaystyle {\begin{aligned}\operatorname {div} \mathbf {A} &=\lim _{V\to 0}{\frac {\iint _{\partial V}\mathbf {A} \cdot d\mathbf {S} }{\iiint _{V}dV}}\\&={\frac {A_{r}(r+dr)(r+dr)\,d\theta \,(r+dr)\sin \theta \,d\phi -A_{r}(r)r\,d\theta \,r\sin \theta \,d\phi +A_{\theta }(\theta +d\theta )\sin(\theta +d\theta )r\,dr\,d\phi -A_{\theta }(\theta )\sin(\theta )r\,dr\,d\phi +A_{\phi }(\phi +d\phi )r\,dr\,d\theta -A_{\phi }(\phi )r\,dr\,d\theta }{dr\,r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r^{2}}}{\frac {\partial (r^{2}A_{r})}{\partial r}}+{\frac {1}{r\sin \theta }}{\frac {\partial (A_{\theta }\sin \theta )}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial A_{\phi }}{\partial \phi }}\end{aligned}}}

( curl ⁡ A ) r = lim S ⊥ r ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A θ ( ϕ ) r d θ + A ϕ ( θ + d θ ) r sin ⁡ ( θ + d θ ) d ϕ − A θ ( ϕ + d ϕ ) r d θ − A ϕ ( θ ) r sin ⁡ ( θ ) d ϕ r d θ r sin ⁡ θ d ϕ = 1 r sin ⁡ θ ∂ ( A ϕ sin ⁡ θ ) ∂ θ − 1 r sin ⁡ θ ∂ A θ ∂ ϕ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{r}=\lim _{S^{\perp {\boldsymbol {\hat {r}}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\theta }(\phi )r\,d\theta +A_{\phi }(\theta +d\theta )r\sin(\theta +d\theta )\,d\phi -A_{\theta }(\phi +d\phi )r\,d\theta -A_{\phi }(\theta )r\sin(\theta )\,d\phi }{r\,d\theta \,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {1}{r\sin \theta }}{\frac {\partial A_{\theta }}{\partial \phi }}\end{aligned}}}

( curl ⁡ A ) θ = lim S ⊥ θ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A ϕ ( r ) r sin ⁡ θ d ϕ + A r ( ϕ + d ϕ ) d r − A ϕ ( r + d r ) ( r + d r ) sin ⁡ θ d ϕ − A r ( ϕ ) d r d r r sin ⁡ θ d ϕ = 1 r sin ⁡ θ ∂ A r ∂ ϕ − 1 r ∂ ( r A ϕ ) ∂ r {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\theta }=\lim _{S^{\perp {\boldsymbol {\hat {\theta }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{\phi }(r)r\sin \theta \,d\phi +A_{r}(\phi +d\phi )\,dr-A_{\phi }(r+dr)(r+dr)\sin \theta \,d\phi -A_{r}(\phi )\,dr}{dr\,r\sin \theta \,d\phi }}\\&={\frac {1}{r\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {1}{r}}{\frac {\partial (rA_{\phi })}{\partial r}}\end{aligned}}}

( curl ⁡ A ) ϕ = lim S ⊥ ϕ ^ → 0 ∫ ∂ S A ⋅ d ℓ ∬ S d S = A r ( θ ) d r + A θ ( r + d r ) ( r + d r ) d θ − A r ( θ + d θ ) d r − A θ ( r ) r d θ r d r d θ = 1 r ∂ ( r A θ ) ∂ r − 1 r ∂ A r ∂ θ {\displaystyle {\begin{aligned}(\operatorname {curl} \mathbf {A} )_{\phi }=\lim _{S^{\perp {\boldsymbol {\hat {\phi }}}}\to 0}{\frac {\int _{\partial S}\mathbf {A} \cdot d\mathbf {\ell } }{\iint _{S}dS}}&={\frac {A_{r}(\theta )\,dr+A_{\theta }(r+dr)(r+dr)\,d\theta -A_{r}(\theta +d\theta )\,dr-A_{\theta }(r)r\,d\theta }{r\,dr\,d\theta }}\\&={\frac {1}{r}}{\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {1}{r}}{\frac {\partial A_{r}}{\partial \theta }}\end{aligned}}}

curl ⁡ A = ( curl ⁡ A ) r r ^ + ( curl ⁡ A ) θ θ ^ + ( curl ⁡ A ) ϕ ϕ ^ = 1 r sin ⁡ θ ( ∂ ( A ϕ sin ⁡ θ ) ∂ θ − ∂ A θ ∂ ϕ ) r ^ + 1 r ( 1 sin ⁡ θ ∂ A r ∂ ϕ − ∂ ( r A ϕ ) ∂ r ) θ ^ + 1 r ( ∂ ( r A θ ) ∂ r − ∂ A r ∂ θ ) ϕ ^ {\displaystyle {\begin{aligned}\operatorname {curl} \mathbf {A} &=(\operatorname {curl} \mathbf {A} )_{r}\,{\hat {\boldsymbol {r}}}+(\operatorname {curl} \mathbf {A} )_{\theta }\,{\hat {\boldsymbol {\theta }}}+(\operatorname {curl} \mathbf {A} )_{\phi }\,{\hat {\boldsymbol {\phi }}}\\&={\frac {1}{r\sin \theta }}\left({\frac {\partial (A_{\phi }\sin \theta )}{\partial \theta }}-{\frac {\partial A_{\theta }}{\partial \phi }}\right){\hat {\boldsymbol {r}}}+{\frac {1}{r}}\left({\frac {1}{\sin \theta }}{\frac {\partial A_{r}}{\partial \phi }}-{\frac {\partial (rA_{\phi })}{\partial r}}\right){\hat {\boldsymbol {\theta }}}+{\frac {1}{r}}\left({\frac {\partial (rA_{\theta })}{\partial r}}-{\frac {\partial A_{r}}{\partial \theta }}\right){\hat {\boldsymbol {\phi }}}\end{aligned}}}

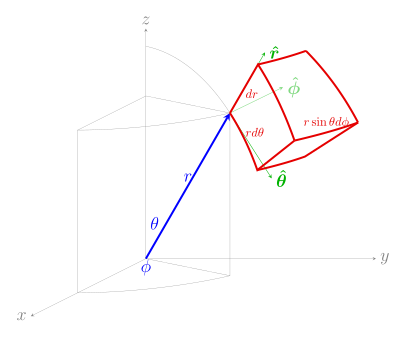
Unit vector conversion formula

The unit vector of a coordinate parameter u is defined in such a way that a small positive change in u causes the position vector r {\displaystyle \mathbf {r} } to change in u {\displaystyle \mathbf {u} } direction.

Therefore, ∂ r ∂ u = ∂ s ∂ u u {\displaystyle {\frac {\partial {\mathbf {r} }}{\partial u}}={\frac {\partial {s}}{\partial u}}\mathbf {u} } where s is the arc length parameter.

For two sets of coordinate systems u i {\displaystyle u_{i}} and v j {\displaystyle v_{j}} , according to chain rule, d r = ∑ i ∂ r ∂ u i d u i = ∑ i ∂ s ∂ u i u ^ i d u i = ∑ j ∂ s ∂ v j v ^ j d v j = ∑ j ∂ s ∂ v j v ^ j ∑ i ∂ v j ∂ u i d u i = ∑ i ∑ j ∂ s ∂ v j ∂ v j ∂ u i v ^ j d u i . {\displaystyle d\mathbf {r} =\sum _{i}{\frac {\partial \mathbf {r} }{\partial u_{i}}}\,du_{i}=\sum _{i}{\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}du_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\,dv_{j}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\hat {\mathbf {v} }}_{j}\sum _{i}{\frac {\partial v_{j}}{\partial u_{i}}}\,du_{i}=\sum _{i}\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}\,du_{i}.}

Now, we isolate the i {\displaystyle i} component. For i ≠ k {\displaystyle i{\neq }k} , let d u k = 0 {\displaystyle \mathrm {d} u_{k}=0} . Then divide on both sides by d u i {\displaystyle \mathrm {d} u_{i}} to get: ∂ s ∂ u i u ^ i = ∑ j ∂ s ∂ v j ∂ v j ∂ u i v ^ j . {\displaystyle {\frac {\partial s}{\partial u_{i}}}{\hat {\mathbf {u} }}_{i}=\sum _{j}{\frac {\partial s}{\partial v_{j}}}{\frac {\partial v_{j}}{\partial u_{i}}}{\hat {\mathbf {v} }}_{j}.}

See also

References

  1. ^ Griffiths, David J. (2012). Introduction to Electrodynamics. Pearson. ISBN 978-0-321-85656-2.
  2. Arfken, George; Weber, Hans; Harris, Frank (2012). Mathematical Methods for Physicists (Seventh ed.). Academic Press. p. 192. ISBN 9789381269558.
  3. Weisstein, Eric W. "Convective Operator". Mathworld. Retrieved 23 March 2011.
  4. Fernández-Guasti, M. (2012). "Green's Second Identity for Vector Fields". ISRN Mathematical Physics. 2012. Hindawi Limited: 1–7. doi:10.5402/2012/973968. ISSN 2090-4681.

External links

Categories: