This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
The network of the human nervous system is composed of nodes (for example, neurons) that are connected by links (for example, synapses). The connectivity may be viewed anatomically, functionally, or electrophysiologically. These are presented in several Misplaced Pages articles that include Connectionism (a.k.a. Parallel Distributed Processing (PDP)), Biological neural network, Artificial neural network (a.k.a. Neural network), Computational neuroscience, as well as in several books by Ascoli, G. A. (2002), Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011), Gerstner, W., & Kistler, W. (2002), and David Rumelhart, McClelland, J. L., and PDP Research Group (1986) among others. The focus of this article is a comprehensive view of modeling a neural network (technically neuronal network based on neuron model). Once an approach based on the perspective and connectivity is chosen, the models are developed at microscopic (ion and neuron), mesoscopic (functional or population), or macroscopic (system) levels. Computational modeling refers to models that are developed using computing tools.
Introduction
The nervous system consists of networks made up of neurons and synapses connected to and controlling tissues as well as impacting human thoughts and behavior. In modeling neural networks of the nervous system one has to consider many factors. The brain and the neural network should be considered as an integrated and self-contained firmware system that includes hardware (organs), software (programs), memory (short term and long term), database (centralized and distributed), and a complex network of active elements (such as neurons, synapses, and tissues) and passive elements (such as parts of visual and auditory system) that carry information within and in-and-out of the body.
Although highly sophisticated computer systems have been developed and used in all walks of life, they are nowhere close to the human system in hardware and software capabilities. So, scientists have been at work to understand the human operation system and try to simulate its functionalities. In order to accomplish this, one needs to model its components and functions and validate its performance with real life. Computational models of a well simulated nervous system enable learning the nervous system and apply it to real life problem solutions.
It is hypothesized that the elementary biological unit is an active cell, called neuron, and the human machine is run by a vast network that connects these neurons, called neural (or neuronal) network. The neural network is integrated with the human organs to form the human machine comprising the nervous system.
Network characteristics
See also: Biological neural networksThe basic structural unit of the neural network is connectivity of one neuron to another via an active junction, called synapse. Neurons of widely divergent characteristics are connected to each other via synapses, whose characteristics are also of diverse chemical and electrical properties. In presenting a comprehensive view of all possible modeling of the brain and neural network, an approach is to organize the material based on the characteristics of the networks and the goals that need to be accomplished. The latter could be either for understanding the brain and the nervous system better or to apply the knowledge gained from the total or partial nervous system to real world applications such as artificial intelligence, Neuroethics or improvements in medical science for society.
Network connectivity and models
On a high level representation, the neurons can be viewed as connected to other neurons to form a neural network in one of three ways. A specific network can be represented as a physiologically (or anatomically) connected network and modeled that way. There are several approaches to this (see Ascoli, G.A. (2002) Sporns, O. (2007), Connectionism, Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986), Arbib, M. A. (2007)). Or, it can form a functional network that serves a certain function and modeled accordingly (Honey, C. J., Kotter, R., Breakspear, R., & Sporns, O. (2007), Arbib, M. A. (2007)). A third way is to hypothesize a theory of the functioning of the biological components of the neural system by a mathematical model, in the form of a set of mathematical equations. The variables of the equation are some or all of the neurobiological properties of the entity being modeled, such as the dimensions of the dendrite or the stimulation rate of action potential along the axon in a neuron. The mathematical equations are solved using computational techniques and the results are validated with either simulation or experimental processes. This approach to modeling is called computational neuroscience. This methodology is used to model components from the ionic level to system level of the brain. This method is applicable for modeling integrated system of biological components that carry information signal from one neuron to another via intermediate active neurons that can pass the signal through or create new or additional signals. The computational neuroscience approach is extensively used and is based on two generic models, one of cell membrane potential Goldman (1943) and Hodgkin and Katz (1949), and the other based on Hodgkin-Huxley model of action potential (information signal).
Modeling levels
Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) classify the biological model of neuroscience into nine levels from ion channels to nervous system level based on size and function. Table 1 is based on this for neuronal networks.
| Level | Size | Description and Functions |
|---|---|---|
| Nervous system | > 1 m | Total system controlling thought, behavior, and sensory & motor functions |
| Subsystem | 10 cm | Subsystem associated with one or more functions |
| Neural network | 1 cm | Neural networks for system, subsystem, and functions |
| Microcircuit | 1 mm | Networks of multilevel neurons, e.g., visual subsystem |
| Neuron | 100 μm | Elementary biological unit of neuronal network |
| Dendric subunit | 10 μm | Arbor of receptors in neuron |
| Synapse | 1 μm | Junction or connectivity between neurons |
| Signalling pathway | 1 nm | Link between connecting neurons |
| Ion channels | 1 pm | Channels that act as gateway causing voltage change |
Sporns, O. (2007) presents in his article on brain connectivity, modeling based on structural and functional types. A network that connects at neuron and synaptic level falls into the microscale. If the neurons are grouped into population of columns and minicolumns, the level is defined as mesoscale. The macroscale representation considers the network as regions of the brain connected by inter-regional pathways.
Arbib, M. A. (2007) considers in the modular model, a hierarchical formulation of the system into modules and submodules.
Signaling modes
The neuronal signal comprises a stream of short electrical pulses of about 100 millivolt amplitude and about 1 to 2 millisecond duration (Gerstner, W., & Kistler, W. (2002) Chapter 1). The individual pulses are action potentials or spikes and the chain of pulses is called spike train. The action potential does not contain any information. A combination of the timing of the start of the spike train, the rate or frequency of the spikes, and the number and pattern of spikes in the spike train determine the coding of the information content or the signal message.
The neuron cell has three components – dendrites, soma, and axon as shown in Figure 1. Dendrites, which have the shape of a tree with branches, called arbor, receive the message from other neurons with which the neuron is connected via synapses. The action potential received by each dendrite from the synapse is called the postsynaptic potential. The cumulative sum of the postsynaptic potentials is fed to the soma. The ionic components of the fluid inside and outside maintain the cell membrane at a resting potential of about 65 millivolts. When the cumulative postsynaptic potential exceeds the resting potential, an action potential is generated by the cell body or soma and propagated along the axon. The axon may have one or more terminals and these terminals transmit neurotransmitters to the synapses with which the neuron is connected. Depending on the stimulus received by the dendrites, soma may generate one or more well-separated action potentials or spike train. If the stimulus drives the membrane to a positive potential, it is an excitatory neuron; and if it drives the resting potential further in the negative direction, it is an inhibitory neuron.

The generation of the action potential is called the "firing". The firing neuron described above is called a spiking neuron. We will model the electrical circuit of the neuron in Section 3.6. There are two types of spiking neurons. If the stimulus remains above the threshold level and the output is a spike train, it is called the Integrate-and-Fire (IF) neuron model. If output is modeled as dependent on the impulse response of the circuit, then it is called the Spike Response Model (SRM) (Gestner, W. (1995)).
The spiking neuron model assumes that frequency (inverse of the rate at which spikes are generated) of spiking train starts at 0 and increases with the stimulus current. There is another hypothetical model that formulates the firing to happen at the threshold, but there is a quantum jump in frequency in contrast to smooth rise in frequency as in the spiking neuron model. This model is called the rate model. Gerstner, W., & Kistler, W. (2002), and Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) are good sources for a detailed treatment of spiking neuron models and rate neuron models.
Biological vs. artificial neural network
The concept of artificial neural network (ANN) was introduced by McCulloch, W. S. & Pitts, W. (1943) for models based on behavior of biological neurons. Norbert Wiener (1961) gave this new field the popular name of cybernetics, whose principle is the interdisciplinary relationship among engineering, biology, control systems, brain functions, and computer science. With the computer science field advancing, the von Neumann-type computer was introduced early in the neuroscience study. But it was not suitable for symbolic processing, nondeterministic computations, dynamic executions, parallel distributed processing, and management of extensive knowledge bases, which are needed for biological neural network applications; and the direction of mind-like machine development changed to a learning machine. Computing technology has since advanced extensively and computational neuroscience is now able to handle mathematical models developed for biological neural network. Research and development are progressing in both artificial and biological neural networks including efforts to merge the two.
Nervous system models
Evolutionary brain model
See also: Triune brainThe "triune theory of the brain" McLean, P. (2003) is one of several models used to theorize the organizational structure of the brain. The most ancient neural structure of the brain is the brain stem or "lizard brain". The second phase is limbic or paleo-mammalian brain and performs the four functions needed for animal survival – fighting, feeding, fleeing, and fornicating. The third phase is the neocortex or the neo-mammalian brain. The higher cognitive functions which distinguish humans from other animals are primarily in the cortex. The reptilian brain controls muscles, balance, and autonomic functions, such as breathing and heartbeat. This part of the brain is active, even in deep sleep. The limbic system includes the hypothalamus, hippocampus, and amygdala. The neocortex includes the cortex and the cerebrum. It corresponds to the brain of primates and, specifically, the human species. Each of the three brains is connected by nerves to the other two, but each seems to operate as its own brain system with distinct capacities. (See illustration in Triune brain.)
PDP / connectionist model
See also: ConnectionismThe connectionist model evolved out of Parallel Distributed Processing framework that formulates a metatheory from which specific models can be generated for specific applications. PDP approach (Rumelhart, J. L., McClelland, J. L., and PDP Research Group (1986)) is a distributed parallel processing of many inter-related operations, somewhat similar to what's happening in the human nervous system. The individual entities are defined as units and the units are connected to form a network. Thus, in the application to nervous system, one representation could be such that the units are the neurons and the links are the synapses.
Brain connectivity model
There are three types of brain connectivity models of a network (Sporns, O. (2007)). "Anatomical (or structural) connectivity" describes a network with anatomical links having specified relationship between connected "units". If the dependent properties are stochastic, it is defined as "functional connectivity". "Effective connectivity" has causal interactions between distinct units in the system. As stated earlier, brain connectivity can be described at three levels. At microlevel, it connects neurons through electrical or chemical synapses. A column of neurons can be considered as a unit in the mesolevel and regions of the brain comprising a large number of neurons and neuron populations as units in the macrolevel. The links in the latter case are the inter-regional pathways, forming large-scale connectivity.

Figure 2 shows the three types of connectivity. The analysis is done using the directed graphs (see Sporns, O. (2007) and Hilgetag, C. C. (2002)). In the structural brain connectivity type, the connectivity is a sparse and directed graph. The functional brain connectivity has bidirectional graphs. The effective brain connectivity is bidirectional with interactive cause and effect relationships. Another representation of the connectivity is by matrix representation (See Sporns, O. (2007)). Hilgetag, C. C. (2002) describes the computational analysis of brain connectivity.
Modular models of brain function
Arbib, M. A. (2007) describes the modular models as follows. "Modular models of the brain aid the understanding of a complex system by decomposing it into structural modules (e.g., brain regions, layers, columns) or functional modules (schemas) and exploring the patterns of competition and cooperation that yield the overall function." This definition is not the same as that defined in functional connectivity. The modular approach is intended to build cognitive models and is, in complexity, between the anatomically defined brain regions (defined as macrolevel in brain connectivity) and the computational model at the neuron level.
There are three views of modules for modeling. They are (1) modules for brain structures, (2) modules as schemas, and (3) modules as interfaces. Figure 3 presents the modular design of a model for reflex control of saccades (Arbib, M. A. (2007)). It involves two main modules, one for superior colliculus (SC), and one for brainstem. Each of these is decomposed into submodules, with each submodule defining an array of physiologically defined neurons. In Figure 3(b) the model of Figure 3(a) is embedded into a far larger model which embraces various regions of cerebral cortex (represented by the modules Pre-LIP Vis, Ctx., LIP, PFC, and FEF), thalamus, and basal ganglia. While the model may indeed be analyzed at this top level of modular decomposition, we need to further decompose basal ganglia, BG, as shown in Figure 3(c) if we are to tease apart the role of dopamine in differentially modulating (the 2 arrows shown arising from SNc) the direct and indirect pathways within the basal ganglia (Crowley, M. (1997)). Neural Simulation Language (NSL) has been developed to provide a simulation system for large-scale general neural networks. It provides an environment to develop an object-oriented approach to brain modeling. NSL supports neural models having as basic data structure neural layers with similar properties and similar connection patterns. Models developed using NSL are documented in Brain Operation Database (BODB) as hierarchically organized modules that can be decomposed into lower levels.
Artificial neural networks
Main articles: Neural network and Artificial neural networkAs mentioned in Section 2.4, development of artificial neural network (ANN), or neural network as it is now called, started as simulation of biological neuron network and ended up using artificial neurons. Major development work has gone into industrial applications with learning process. Complex problems were addressed by simplifying the assumptions. Algorithms were developed to achieve a neurological related performance, such as learning from experience. Since the background and overview have been covered in the other internal references, the discussion here is limited to the types of models. The models are at the system or network level.
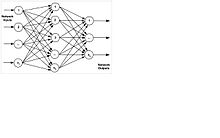
The four main features of an ANN are topology, data flow, types of input values, and forms of activation (Meireles, M. R. G. (2003), Munakata, T. (1998)). Topology can be multilayered, single-layered, or recurrent. Data flow can be recurrent with feedback or non-recurrent with feedforward model. The inputs are binary, bipolar, or continuous. The activation is linear, step, or sigmoid. Multilayer Perceptron (MLP) is the most popular of all the types, which is generally trained with back-propagation of error algorithm. Each neuron output is connected to every neuron in subsequent layers connected in cascade and with no connections between neurons in the same layer. Figure 4 shows a basic MLP topology (Meireles, M. R. G. (2003)), and a basic telecommunication network (Subramanian, M. (2010)) that most are familiar with. We can equate the routers at the nodes in telecommunication network to neurons in MLP technology and the links to synapses.

Computational neuron models
See also: Computational neuroscienceComputational neuroscience is an interdisciplinary field that combines engineering, biology, control systems, brain functions, physical sciences, and computer science. It has fundamental development models done at the lower levels of ions, neurons, and synapses, as well as information propagation between neurons. These models have established the enabling technology for higher-level models to be developed. They are based on chemical and electrical activities in the neurons for which electrical equivalent circuits are generated. A simple model for the neuron with predominantly potassium ions inside the cell and sodium ions outside establishes an electric potential on the membrane under equilibrium, i.e., no external activity, condition. This is called the resting membrane potential, which can be determined by Nernst Equation (Nernst, W. (1888)). An equivalent electrical circuit for a patch of membrane, for example an axon or dendrite, is shown in Figure 5. EK and ENa are the potentials associated with the potassium and sodium channels respectively and RK and RNa are the resistances associated with them. C is the capacitance of the membrane and I is the source current, which could be the test source or the signal source (action potential). The resting potential for potassium-sodium channels in a neuron is about -65 millivolts.

The membrane model is for a small section of the cell membrane; for larger sections it can be extended by adding similar sections, called compartments, with the parameter values being the same or different. The compartments are cascaded by a resistance, called axial resistance. Figure 6 shows a compartmental model of a neuron that is developed over the membrane model. Dendrites are the postsynaptic receptors receiving inputs from other neurons; and the axon with one or more axon terminals transmits neurotransmitters to other neurons.

The second building block is the Hodgkin-Huxley (HH) model of the action potential. When the membrane potential from the dendrites exceeds the resting membrane potential, a pulse is generated by the neuron cell and propagated along the axon. This pulse is called the action potential and HH model is a set of equations that is made to fit the experimental data by the design of the model and the choice of the parameter values.
Models for more complex neurons containing other types of ions can be derived by adding to the equivalent circuit additional battery and resistance pairs for each ionic channel. The ionic channel could be passive or active as they could be gated by voltage or be ligands. The extended HH model has been developed to handle the active channel situation.
Although there are neurons that are physiologically connected to each other, information is transmitted at most of the synapses by chemical process across a cleft. Synapses are also computationally modeled. The next level of complexity is that of stream of action potentials, which are generated, whose pattern contains the coding information of the signal being transmitted. There are basically two types of action potentials, or spikes as they are called, that are generated. One is "integrate-and-fire" (the one we have so far addressed) and the other which is rate based. The latter is a stream whose rate varies. The signal going across the synapses could be modeled either as a deterministic or a stochastic process based on the application (See Section 3.7). Another anatomical complication is when a population of neurons, such as a column of neurons in visionary system, needs to be handled. This is done by considering the collective behavior of the group (Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, F. T., & Northoff, G. (2002)).
Spiking neuron models
See also: Spiking neural networkThe action potential or the spike does not itself carry any information. It is the stream of spikes, called spike train, that carry the information in its number and pattern of spikes and timing of spikes. The postsynaptic potential can be either positive, the excitatory synapse or negative, inhibitory synapse. In modeling, the postsynaptic potentials received by the dendrites in the postsynaptic neuron are integrated and when the integrated potential exceeds the resting potential, the neuron fires an action potential along its axon. This model is the Integrate-and-Fire (IF) model that was mentioned in Section 2.3. Closely related to IF model is a model called Spike Response Model (SRM) (Gerstner, W. (1995) Pages 738-758) that is dependent on impulse function response convoluted with the input stimulus signal. This forms a base for a large number of models developed for spiking neural networks.
The IF and SR model of spike train occurs in Type I neurons, in which the spike rate or spike frequency of the occurrence increases smoothly with the increase in stimulus current starting from zero. Another phenomenon of spike train generation happens in Type II neurons, where firing occurs at the resting potential threshold, but with a quantum jump to a non-zero frequency. Models have been developed using the rate (frequency) of the spike train and are called rate-based models.
What is important for understanding the functions of the nervous system is how the message is coded and transported by the action potential in the neuron. There are two theories on how the signal that is being propagated is coded in the spikes as to whether it is pulse code or rate code. In the former, it is the time delay of the first spike from the time of stimulus as seen by the postsynaptic receiver that determines the coding. In the rate code, it is average rate of the spike that influences the coding. It is not certain as to which is really the actual physiological phenomenon in each case. However, both cases can be modeled computationally and the parameters varied to match the experimental result. The pulse mode is more complex to model and numerous detailed neuron models and population models are described by Gerstner and Kistler in Parts I and II of Gerstner, W., & Kistler, W. (2002) and Chapter 8 of Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011). Another important characteristic associated with SR model is the spike-time-dependent-plasticity. It is based on Hebb's postulate on plasticity of synapse, which states that "the neurons that fire together wire together". This causes the synapse to be a long-term potentiation (LTP) or long-term depression (LTD). The former is the strengthening of the synapse between two neurons if the postsynaptic spike temporally follows immediately after the presynaptic spike. Latter is the case if it is reverse, i.e., the presynaptic spike occurs after the postsynaptic spike. Gerstner, W. & Kistler, W. (2002) in Chapter 10 and Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) in Chapter 7 discuss the various models related to Hebbian models on plasticity and coding.
Nervous system network models
The challenge involved in developing models for small, medium, and large networks is one of reducing the complexity by making valid simplifying assumptions in and extending the Hodgkin-Huxley neuronal model appropriately to design those models ( see Chapter 9 of Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011), Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, F. T., & Northoff, G. (2002), and Chapter 9 of Gerstner, W., & Kistler, W. (2002)). Network models can be classified as either network of neurons propagating through different levels of cortex or neuron populations interconnected as multilevel neurons. The spatial positioning of neuron could be 1-, 2- or 3-dimensional; the latter ones are called small-world networks as they are related to local region. The neuron could be either excitatory or inhibitory, but not both. Modeling design depends on whether it is artificial neuron or biological neuron of neuronal model. Type I or Type II choice needs to be made for the firing mode. Signaling in neurons could be rate-based neurons, spiking response neurons, or deep-brain stimulated. The network can be designed as feedforward or recurrent type. The network needs to be scaled for the computational resource capabilities. Large-scale thalamocortical systems are handled in the manner of the Blue Brain project (Markam, H. (2006)).
Nervous system development models
No generalized modeling concepts exist for modeling the development of anatomical physiology and morphology similar to the one of behavior of neuronal network, which is based on HH model. Shankle, W. R., Hara, J., Fallon, J. H., and Landing, B. H. (2002) describe the application of neuroanatomical data of the developing human cerebral cortex to computational models. Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. (2011) discuss aspects of the nervous system of computational modeling in the development of nerve cell morphology, cell physiology, cell patterning, patterns of ocular dominance, and connection between nerve cell and muscle, and retinotopic maps. Carreira-Perpinan, M. A. & Goodhill, G. J. (2002) deal with the optimization of the computerized models of the visual cortex.
Modeling tools
With the enormous number of models that have been created, tools have been developed for dissemination of the information, as well as platforms to develop models. Several generalized tools, such as GENESIS, NEURON, XPP, and NEOSIM are available and are discussed by Hucka, M. (2002).
See also
References
- ^ Ascoli, G.A. (Ed). (2002). Computational Neuroanatomy: Principles and Methods. Totowa, New Jersey: Humana Press.
- ^ Sterratt, D., Graham, B., Gillies, A., & Willshaw, D. Ch 9 (2011). Principles of Computational Modelling in Neuroscience, Chapter 9. Cambridge, U.K.: Cambridge University Press.
- ^ Gerstner, W. and Kistler, W. (2002). Spiking Neuron Models, Chapter 9. Cambridge, U. K.: Cambridge University Press.
- ^ Rumelrhart, D., McClelland, J. L., & the PDP Research Group (1986). Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations. Cambridge: The MIT Press.
- Ramon y Cajol, S. (1894). Textura del Sistema Nervioso del Hombre u los Vertebrados. English translation by Swanson, N. & L. W. (1994). New York: Oxford University Press.
- ^ Sporns, Olaf (2007). "Brain connectivity". Scholarpedia. 2 (10): 4695. Bibcode:2007SchpJ...2.4695S. doi:10.4249/scholarpedia.4695.
- ^ Arbib, Michael (2007). "Modular models of brain function". Scholarpedia. 2 (3): 1869. Bibcode:2007SchpJ...2.1869A. doi:10.4249/scholarpedia.1869.
- Honey, C. J.; Kotter, R.; Breakspear, M.; Sporns, O. (2007-06-04). "Network structure of cerebral cortex shapes functional connectivity on multiple time scales". Proceedings of the National Academy of Sciences USA. 104 (24). Proceedings of the National Academy of Sciences: 10240–10245. Bibcode:2007PNAS..10410240H. doi:10.1073/pnas.0701519104. ISSN 0027-8424. PMC 1891224. PMID 17548818.
- Goldman, David E. (1943-09-20). "Potential, impedance, and rectification in membrane". The Journal of General Physiology. 27 (1). Rockefeller University Press: 37–60. doi:10.1085/jgp.27.1.37. ISSN 1540-7748. PMC 2142582. PMID 19873371.
- Hodgkin, A. L.; Katz, B. (1949). "The effect of sodium ions on the electrical activity of the giant axon of the squid". The Journal of Physiology. 108 (1). Wiley: 37–77. doi:10.1113/jphysiol.1949.sp004310. ISSN 0022-3751. PMC 1392331. PMID 18128147.
- Hodgkin, A. L.; Huxley, A. F. (1952-04-28). "Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo". The Journal of Physiology. 116 (4). Wiley: 449–472. doi:10.1113/jphysiol.1952.sp004717. ISSN 0022-3751. PMC 1392213. PMID 14946713.
- Hodgkin, A. L.; Huxley, A. F. (1952-04-28). "The components of membrane conductance in the giant axon of Loligo". The Journal of Physiology. 116 (4). Wiley: 473–496. doi:10.1113/jphysiol.1952.sp004718. ISSN 0022-3751. PMC 1392209. PMID 14946714.
- Hodgkin, A. L.; Huxley, A. F. (1952-04-28). "The dual effect of membrane potential on sodium conductance in the giant axon of Loligo". The Journal of Physiology. 116 (4). Wiley: 497–506. doi:10.1113/jphysiol.1952.sp004719. ISSN 0022-3751. PMC 1392212. PMID 14946715.
- Hodgkin, A. L.; Huxley, A. F. (1952-08-28). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology. 117 (4). Wiley: 500–544. doi:10.1113/jphysiol.1952.sp004764. ISSN 0022-3751. PMC 1392413. PMID 12991237.
- ^ Gerstner, Wulfram (1995-01-01). "Time structure of the activity in neural network models". Physical Review E. 51 (1). American Physical Society (APS): 738–758. Bibcode:1995PhRvE..51..738G. doi:10.1103/physreve.51.738. ISSN 1063-651X. PMID 9962697.
- McCulloch, Warren S.; Pitts, Walter (1943). "A logical calculus of the ideas immanent in nervous activity". Bulletin of Mathematical Biophysics. 5 (4). Springer Science and Business Media LLC: 115–133. doi:10.1007/bf02478259. ISSN 0007-4985.
- Wiener, Norbert (1948). Cybernetics, or Control and Communication in the Animal and the Machine. Cambridge: MIT Press.
- Mclean, P. (2003). Triune Brain. http://malankazlev.com/kheper/topics/intelligence/MacLean.htm
- ^ Hilgetag, C. C. (2002). Ascoli, G. A. (Ed), Computational Methods for the Analysis of Brain Connectivity. Computational Neuroanatomy: Principles and Methods, Chapter 14. Totowa, New Jersey: Humana Press.
- Crowley, M. (1997). Modeling Saccadic Motor Control: Normal Function. Sensory Remapping and Basal Ganglia Dysfunction. Unpublished Ph.D. thesis, University of Southern California.
- ^ Meireles, M.R.G.; Almeida, P.E.M.; Simoes, M.G. (2003). "A comprehensive review for industrial applicability of artificial neural networks". IEEE Transactions on Industrial Electronics. 50 (3). Institute of Electrical and Electronics Engineers (IEEE): 585–601. doi:10.1109/tie.2003.812470. ISSN 0278-0046. S2CID 11278899.
- Munakata, T. (1998). Fundamentals of the New Artificial Intelligence — Beyond Traditional Paradigms. Berlin, Germany: Springer-Verlag.
- Subramanian, M.(2010): Network Management: Principles and Practice, Chapter 1, Pearson, Chennai
- Nernst, W. (1888-01-01). "Zur Kinetik der in Lösung befindlichen Körper". Zeitschrift für Physikalische Chemie (in German). 2U (1). Walter de Gruyter GmbH: 613–637. doi:10.1515/zpch-1888-0274. ISSN 2196-7156. S2CID 202552528.
- ^ Kotter, R., Nielson, P., Dyhrfjeld-Johnson, J., Sommer, F. T., & Northoff, G. (2002). Multi-level Neuron and Network Modeling in Computational Neuroanatomy. Ascoli, G. A (Ed). Computational Neuroanatomy: Principles and Methods, Chapter 16 363-364. Totawa, New Jersey: Humana Press.
- Markram, Henry (2006). "The Blue Brain Project". Nature Reviews Neuroscience. 7 (2). Springer Science and Business Media LLC: 153–160. doi:10.1038/nrn1848. ISSN 1471-003X. PMID 16429124. S2CID 15752137.
- Shankle, W. R., Hara, J., Fallon, J. H., and Landing, B. H. (2002). How the Brain Develops and How It functions. Ascoli, G A. (Ed) Computational Neuroanatomy: Principles and Methods, Chapter 18. Totawa, New Jersey: Humana Press.
- Carreira-Perpinan, M. A., & Goodhill, G. J. (2002). Development of columnar structures in Visual Cortex. In Ascoli, G. A. (Ed), Computational Neuroanatomy: Principles and Methods, Chapter 15. Totowa, New Jersey: Humana Press.
- Hucka, M., Shankar, K., Beeman, D., and Bower, J. M. (2002). Ascoli, G. A (Ed), The Modeler's Workspace. Computational Neuroanatomy: Principles and Methods, Chapter 5. Totowa, New Jersey: Humana Press.