

 From left to right, top to bottom: A tesseract or four-dimensional hypercube, the graph of a binary function, a trefoil knot (a kind of mathematical knot), and a common hierarchy of sets of numbers.
From left to right, top to bottom: A tesseract or four-dimensional hypercube, the graph of a binary function, a trefoil knot (a kind of mathematical knot), and a common hierarchy of sets of numbers.
A mathematical object is an abstract concept arising in mathematics. Typically, a mathematical object can be a value that can be assigned to a symbol, and therefore can be involved in formulas. Commonly encountered mathematical objects include numbers, expressions, shapes, functions, and sets. Mathematical objects can be very complex; for example, theorems, proofs, and even formal theories are considered as mathematical objects in proof theory.
In Philosophy of mathematics, the concept of "mathematical objects" touches on topics of existence, identity, and the nature of reality. In metaphysics, objects are often considered entities that possess properties and can stand in various relations to one another. Philosophers debate whether mathematical objects have an independent existence outside of human thought (realism), or if their existence is dependent on mental constructs or language (idealism and nominalism). Objects can range from the concrete: such as physical objects usually studied in applied mathematics, to the abstract, studied in pure mathematics. What constitutes an "object" is foundational to many areas of philosophy, from ontology (the study of being) to epistemology (the study of knowledge). In mathematics, objects are often seen as entities that exist independently of the physical world, raising questions about their ontological status. There are varying schools of thought which offer different perspectives on the matter, and many famous mathematicians and philosophers each have differing opinions on which is more correct.
In philosophy of mathematics
Quine-Putnam indispensability
Quine-Putnam indispensability is an argument for the existence of mathematical objects based on their unreasonable effectiveness in the natural sciences. Every branch of science relies largely on large and often vastly different areas of mathematics. From physics' use of Hilbert spaces in quantum mechanics and differential geometry in general relativity to biology's use of chaos theory and combinatorics (see mathematical biology), not only does mathematics help with predictions, it allows these areas to have an elegant language to express these ideas. Moreover, it is hard to imagine how areas like quantum mechanics and general relativity could have developed without their assistance from mathematics, and therefore, one could argue that mathematics is indispensable to these theories. It is because of this unreasonable effectiveness and indispensability of mathematics that philosophers Willard Quine and Hilary Putnam argue that we should believe the mathematical objects for which these theories depend actually exist, that is, we ought to have an ontological commitment to them. The argument is described by the following syllogism:
(Premise 1) We ought to have ontological commitment to all and only the entities that are indispensable to our best scientific theories.
(Premise 2) Mathematical entities are indispensable to our best scientific theories.
(Conclusion) We ought to have ontological commitment to mathematical entities
This argument resonates with a philosophy in applied mathematics called Naturalism (or sometimes Predicativism) which states that the only authoritative standards on existence are those of science.
Schools of thought
Platonism

Platonism asserts that mathematical objects are seen as real, abstract entities that exist independently of human thought, often in some Platonic realm. Just as physical objects like electrons and planets exist, so do numbers and sets. And just as statements about electrons and planets are true or false as these objects contain perfectly objective properties, so are statements about numbers and sets. Mathematicians discover these objects rather than invent them. (See also: Mathematical Platonism)
Some some notable platonists include:
- Plato: The ancient Greek philosopher who, though not a mathematician, laid the groundwork for Platonism by positing the existence of an abstract realm of perfect forms or ideas, which influenced later thinkers in mathematics.
- Kurt Gödel: A 20th-century logician and mathematician, Gödel was a strong proponent of mathematical Platonism, and his work in model theory was a major influence on modern platonism
- Roger Penrose: A contemporary mathematical physicist, Penrose has argued for a Platonic view of mathematics, suggesting that mathematical truths exist in a realm of abstract reality that we discover.
Nominalism
Nominalism denies the independent existence of mathematical objects. Instead, it suggests that they are merely convenient fictions or shorthand for describing relationships and structures within our language and theories. Under this view, mathematical objects do not have an existence beyond the symbols and concepts we use.
Some notable nominalists include:
- Nelson Goodman: A philosopher known for his work in the philosophy of science and nominalism. He argued against the existence of abstract objects, proposing instead that mathematical objects are merely a product of our linguistic and symbolic conventions.
- Hartry Field: A contemporary philosopher who has developed the form of nominalism called "fictionalism," which argues that mathematical statements are useful fictions that do not correspond to any actual abstract objects.
Logicism
Logicism asserts that all mathematical truths can be reduced to logical truths, and all objects forming the subject matter of those branches of mathematics are logical objects. In other words, mathematics is fundamentally a branch of logic, and all mathematical concepts, theorems, and truths can be derived from purely logical principles and definitions. Logicism faced challenges, particularly with the Russillian axioms, the Multiplicative axiom (now called the Axiom of Choice) and his Axiom of Infinity, and later with the discovery of Gödel's incompleteness theorems, which showed that any sufficiently powerful formal system (like those used to express arithmetic) cannot be both complete and consistent. This meant that not all mathematical truths could be derived purely from a logical system, undermining the logicist program.
Some notable logicists include:
- Gottlob Frege: Frege is often regarded as the founder of logicism. In his work, Grundgesetze der Arithmetik (Basic Laws of Arithmetic), Frege attempted to show that arithmetic could be derived from logical axioms. He developed a formal system that aimed to express all of arithmetic in terms of logic. Frege's work laid the groundwork for much of modern logic and was highly influential, though it encountered difficulties, most notably Russell's paradox, which revealed inconsistencies in Frege's system.
- Bertrand Russell: Russell, along with Alfred North Whitehead, further developed logicism in their monumental work Principia Mathematica. They attempted to derive all of mathematics from a set of logical axioms, using a type theory to avoid the paradoxes that Frege's system encountered. Although Principia Mathematica was enormously influential, the effort to reduce all of mathematics to logic was ultimately seen as incomplete. However, it did advance the development of mathematical logic and analytic philosophy.
Formalism
Mathematical formalism treats objects as symbols within a formal system. The focus is on the manipulation of these symbols according to specified rules, rather than on the objects themselves. One common understanding of formalism takes mathematics as not a body of propositions representing an abstract piece of reality but much more akin to a game, bringing with it no more ontological commitment of objects or properties than playing ludo or chess. In this view, mathematics is about the consistency of formal systems rather than the discovery of pre-existing objects. Some philosophers consider logicism to be a type of formalism.
Some notable formalists include:
- David Hilbert: A leading mathematician of the early 20th century, Hilbert is one of the most prominent advocates of formalism as a foundation of mathematics (see Hilbert's program). He believed that mathematics is a system of formal rules and that its truth lies in the consistency of these rules rather than any connection to an abstract reality.
- Hermann Weyl: German mathematician and philosopher who, while not strictly a formalist, contributed to formalist ideas, particularly in his work on the foundations of mathematics. Freeman Dyson wrote that Weyl alone bore comparison with the "last great universal mathematicians of the nineteenth century", Henri Poincaré and David Hilbert.
Constructivism
Mathematical constructivism asserts that it is necessary to find (or "construct") a specific example of a mathematical object in order to prove that an example exists. Contrastingly, in classical mathematics, one can prove the existence of a mathematical object without "finding" that object explicitly, by assuming its non-existence and then deriving a contradiction from that assumption. Such a proof by contradiction might be called non-constructive, and a constructivist might reject it. The constructive viewpoint involves a verificational interpretation of the existential quantifier, which is at odds with its classical interpretation. There are many forms of constructivism. These include Brouwer's program of intutionism, the finitism of Hilbert and Bernays, the constructive recursive mathematics of mathematicians Shanin and Markov, and Bishop's program of constructive analysis. Constructivism also includes the study of constructive set theories such as Constructive Zermelo–Fraenkel and the study of philosophy.
Some notable constructivists include:
- L. E. J. Brouwer: Dutch mathematician and philosopher regarded as one of the greatest mathematicians of the 20th century, known for (among other things) pioneering the intuitionist movement to mathematical logic, and opposition of David Hilbert's formalism movement (see: Brouwer–Hilbert controversy).
- Errett Bishop: American mathematician known for his work on analysis. He is best known for developing constructive analysis in his 1967 Foundations of Constructive Analysis, where he proved most of the important theorems in real analysis using constructivist methods.
Structuralism
Structuralism suggests that mathematical objects are defined by their place within a structure or system. The nature of a number, for example, is not tied to any particular thing, but to its role within the system of arithmetic. In a sense, the thesis is that mathematical objects (if there are such objects) simply have no intrinsic nature.
Some notable structuralists include:
- Paul Benacerraf: A philosopher known for his work in the philosophy of mathematics, particularly his paper "What Numbers Could Not Be," which argues for a structuralist view of mathematical objects.
- Stewart Shapiro: Another prominent philosopher who has developed and defended structuralism, especially in his book Philosophy of Mathematics: Structure and Ontology.
Objects versus mappings
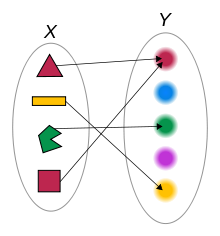
Frege famously distinguished between functions and objects. According to his view, a function is a kind of ‘incomplete’ entity that maps arguments to values, and is denoted by an incomplete expression, whereas an object is a ‘complete’ entity and can be denoted by a singular term. Frege reduced properties and relations to functions and so these entities are not included among the objects. Some authors make use of Frege's notion of ‘object’ when discussing abstract objects. But though Frege's sense of ‘object’ is important, it is not the only way to use the term. Other philosophers include properties and relations among the abstract objects. And when the background context for discussing objects is type theory, properties and relations of higher type (e.g., properties of properties, and properties of relations) may be all be considered ‘objects’. This latter use of ‘object’ is interchangeable with ‘entity.’ It is this more broad interpretation that mathematicians mean when they use the term 'object'.
See also
- Abstract object
- Exceptional object
- Impossible object
- List of mathematical objects
- List of mathematical shapes
- List of shapes
- List of surfaces
- List of two-dimensional geometric shapes
- Mathematical structure
References
Cited sources
- Oxford English Dictionary, s.v. “Mathematical (adj.), sense 2,” September 2024. "Designating or relating to objects apprehended not by sense perception but by thought or abstraction."
- Rettler, Bradley; Bailey, Andrew M. (2024), "Object", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Summer 2024 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Carroll, John W.; Markosian, Ned (2010). An introduction to metaphysics. Cambridge introductions to philosophy (1. publ ed.). Cambridge: Cambridge University Press. ISBN 978-0-521-82629-7.
- Burgess, John, and Rosen, Gideon, 1997. A Subject with No Object: Strategies for Nominalistic Reconstrual of Mathematics. Oxford University Press. ISBN 0198236158
- Falguera, José L.; Martínez-Vidal, Concha; Rosen, Gideon (2022), "Abstract Objects", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Summer 2022 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Horsten, Leon (2023), "Philosophy of Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Winter 2023 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-29
- Colyvan, Mark (2024), "Indispensability Arguments in the Philosophy of Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Summer 2024 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Paseau, Alexander (2016), "Naturalism in the Philosophy of Mathematics", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Winter 2016 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Horsten, Leon (2023), "Philosophy of Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Winter 2023 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Linnebo, Øystein (2024), "Platonism in the Philosophy of Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Summer 2024 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-27
- "Platonism, Mathematical | Internet Encyclopedia of Philosophy". Retrieved 2024-08-28.
- Roibu, Tib (2023-07-11). "Sir Roger Penrose". Geometry Matters. Retrieved 2024-08-27.
- Bueno, Otávio (2020), "Nominalism in the Philosophy of Mathematics", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Fall 2020 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-27
- "Mathematical Nominalism | Internet Encyclopedia of Philosophy". Retrieved 2024-08-28.
- Field, Hartry (2016-10-27). Science without Numbers. Oxford University Press. doi:10.1093/acprof:oso/9780198777915.001.0001. ISBN 978-0-19-877791-5.
- Tennant, Neil (2023), "Logicism and Neologicism", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Winter 2023 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-27
- "Frege, Gottlob | Internet Encyclopedia of Philosophy". Retrieved 2024-08-29.
- Glock, H.J. (2008). What is Analytic Philosophy?. Cambridge University Press. p. 1. ISBN 978-0-521-87267-6. Retrieved 2023-08-28.
- Weir, Alan (2024), "Formalism in the Philosophy of Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Spring 2024 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Simons, Peter (2009). "Formalism". Philosophy of Mathematics. Elsevier. p. 292. ISBN 9780080930589.
- Bell, John L.; Korté, Herbert (2024), "Hermann Weyl", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Summer 2024 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Freeman Dyson (10 March 1956). "Prof. Hermann Weyl, For.Mem.R.S." Nature. 177 (4506): 457–458. Bibcode:1956Natur.177..457D. doi:10.1038/177457a0. S2CID 216075495.
He alone could stand comparison with the last great universal mathematicians of the nineteenth century, Hilbert and Poincaré. ... Now he is dead, the contact is broken, and our hopes of comprehending the physical universe by a direct use of creative mathematical imagination are for the time being ended.
- Bridges, Douglas; Palmgren, Erik; Ishihara, Hajime (2022), "Constructive Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Fall 2022 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Troelstra, Anne Sjerp (1977a). "Aspects of Constructive Mathematics". Handbook of Mathematical Logic. 90: 973–1052. doi:10.1016/S0049-237X(08)71127-3
- Bishop, Errett (1967). Foundations of Constructive Analysis. New York: Academic Press. ISBN 4-87187-714-0.
- "Structuralism, Mathematical | Internet Encyclopedia of Philosophy". Retrieved 2024-08-28.
- Reck, Erich; Schiemer, Georg (2023), "Structuralism in the Philosophy of Mathematics", in Zalta, Edward N.; Nodelman, Uri (eds.), The Stanford Encyclopedia of Philosophy (Spring 2023 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
- Philosophy of Mathematics: Structure and Ontology. Oxford University Press, 1997. ISBN 0-19-513930-5
- Halmos, Paul R. (1974). Naive set theory. Undergraduate texts in mathematics. New York: Springer-Verlag. p. 30. ISBN 978-0-387-90092-6.
- Marshall, William (1953). "Frege's Theory of Functions and Objects". The Philosophical Review. 62 (3): 374–390. doi:10.2307/2182877. ISSN 0031-8108. JSTOR 2182877.
- Hale, Bob (2016), "Abstract objects", Routledge Encyclopedia of Philosophy, London: Routledge, doi:10.4324/9780415249126-n080-1, ISBN 978-0-415-25069-6, retrieved 2024-08-28
- Falguera, José L.; Martínez-Vidal, Concha; Rosen, Gideon (2022), "Abstract Objects", in Zalta, Edward N. (ed.), The Stanford Encyclopedia of Philosophy (Summer 2022 ed.), Metaphysics Research Lab, Stanford University, retrieved 2024-08-28
Further reading
- Azzouni, J., 1994. Metaphysical Myths, Mathematical Practice. Cambridge University Press.
- Burgess, John, and Rosen, Gideon, 1997. A Subject with No Object. Oxford Univ. Press.
- Davis, Philip and Reuben Hersh, 1999 . The Mathematical Experience. Mariner Books: 156–62.
- Gold, Bonnie, and Simons, Roger A., 2011. Proof and Other Dilemmas: Mathematics and Philosophy. Mathematical Association of America.
- Hersh, Reuben, 1997. What is Mathematics, Really? Oxford University Press.
- Sfard, A., 2000, "Symbolizing mathematical reality into being, Or how mathematical discourse and mathematical objects create each other," in Cobb, P., et al., Symbolizing and communicating in mathematics classrooms: Perspectives on discourse, tools and instructional design. Lawrence Erlbaum.
- Stewart Shapiro, 2000. Thinking about mathematics: The philosophy of mathematics. Oxford University Press.
Notes
- See Complex numbers (ℂ), Real numbers (ℝ), Rational numbers (ℚ), Integers (ℤ) and Natural numbers (ℕ)
External links
- Stanford Encyclopedia of Philosophy: "Abstract Objects"—by Gideon Rosen.
- Wells, Charles. "Mathematical Objects".
- AMOF: The Amazing Mathematical Object Factory
- Mathematical Object Exhibit
| Mathematical logic | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| General | |||||||||
| Theorems (list) and paradoxes | |||||||||
| Logics |
| ||||||||
| Set theory |
| ||||||||
| Formal systems (list), language and syntax |
| ||||||||
| Proof theory | |||||||||
| Model theory | |||||||||
| Computability theory | |||||||||
| Related | |||||||||