Misplaced Pages

In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or (in cases where they have the form of a forest of line segments or other curves) opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.

For instance, visibility through a unit square can be blocked by its four boundary edges, with length 4, but a shorter opaque forest blocks visibility across the square with length ${\displaystyle {\sqrt {2}}+{\tfrac {1}{2}}{\sqrt {6}}\approx 2.639}$. It is unproven whether this is the shortest possible opaque set for the square, and for most other shapes this problem similarly remains unsolved. The shortest opaque set for any bounded convex set in the plane has length at most the perimeter of the set, and at least half the perimeter. For the square, a slightly stronger lower bound than half the perimeter is known. Another convex set whose opaque sets are commonly studied is the unit circle, for which the shortest connected opaque set has length ${\displaystyle 2+\pi }$. Without the assumption of connectivity, the shortest opaque set for the circle has length at least ${\displaystyle \pi }$ and at most ${\displaystyle 4.7998}$.

Several published algorithms claiming to find the shortest opaque set for a convex polygon were later shown to be incorrect. Nevertheless, it is possible to find an opaque set with a guaranteed approximation ratio in linear time, or to compute the subset of the plane whose visibility is blocked by a given system of line segments in polynomial time.

Definitions

Every set ${\displaystyle S}$ in the plane blocks the visibility through a superset of ${\displaystyle S}$, its coverage ${\displaystyle C}$. ${\displaystyle C}$ consists of points for which all lines through the point intersect ${\displaystyle S}$. If a given set ${\displaystyle K}$ forms a subset of the coverage of ${\displaystyle S}$, then ${\displaystyle S}$ is said to be an opaque set, barrier, beam detector, or opaque cover for ${\displaystyle K}$. If, additionally, ${\displaystyle S}$ has a special form, consisting of finitely many line segments whose union forms a forest, it is called an opaque forest. There are many possible opaque sets for any given set ${\displaystyle K}$, including ${\displaystyle K}$ itself, and many possible opaque forests. For opaque forests, or more generally for systems of rectifiable curves, their length can be measured in the standard way. For more general point sets, one-dimensional Hausdorff measure can be used, and agrees with the standard length in the cases of line segments and rectifiable curves.

Most research on this problem assumes that the given set ${\displaystyle K}$ is a convex set. When it is not convex but merely a connected set, it can be replaced by its convex hull without changing its opaque sets. Some variants of the problem restrict the opaque set to lie entirely inside or entirely outside ${\displaystyle K}$. In this case, it is called an interior barrier or an exterior barrier, respectively. When this is not specified, the barrier is assumed to have no constraints on its location. Versions of the problem in which the opaque set must be connected or form a single curve have also been considered. It is not known whether every convex set ${\displaystyle P}$ has a shortest opaque set, or whether instead the lengths of its opaque sets might approach an infimum without ever reaching it. Every opaque set for ${\displaystyle P}$ can be approximated arbitrarily closely in length by an opaque forest, and it has been conjectured that every convex polygon has an opaque forest as its shortest opaque set, but this has not been proven.

Bounds

When the region to be covered is a convex set, the length of its shortest opaque set must be at least half its perimeter and at most its perimeter. For some regions, additional improvements to these bounds can be made.

Upper bound

If ${\displaystyle K}$ is a bounded convex set to be covered, then its boundary ${\displaystyle \partial K}$ forms an opaque set whose length is the perimeter ${\displaystyle |\partial K|}$. Therefore, the shortest possible length of an opaque set is at most the perimeter. For sets ${\displaystyle K}$ that are strictly convex, meaning that there are no line segments on the boundary, and for interior barriers, this bound is tight. Every point on the boundary must be contained in the opaque set, because every boundary point has a tangent line through it that cannot be blocked by any other points. The same reasoning shows that for interior barriers of convex polygons, all vertices must be included. Therefore, the minimum Steiner tree of the vertices is the shortest connected opaque set, and the traveling salesperson path of the vertices is the shortest single-curve opaque set. However, for interior barriers of non-polygonal convex sets that are not strictly convex, or for barriers that are not required to be connected, other opaque sets may be shorter; for instance, it is always possible to omit the longest line segment of the boundary. In these cases, the perimeter or Steiner tree length provide an upper bound on the length of an opaque set.

Lower bound

There are several proofs that an opaque set for any convex set ${\displaystyle K}$ must have total length at least ${\displaystyle |\partial K|/2}$, half the perimeter. One of the simplest involves the Crofton formula, according to which the length of any curve is proportional to its expected number of intersection points with a random line from an appropriate probability distribution on lines. It is convenient to simplify the problem by approximating ${\displaystyle K}$ by a strictly convex superset, which can be chosen to have perimeter arbitrarily close to the original set. Then, except for the tangent lines to ${\displaystyle K}$ (which form a vanishing fraction of all lines), a line that intersects ${\displaystyle K}$ crosses its boundary twice. Therefore, if a random line intersects ${\displaystyle K}$ with probability ${\displaystyle p}$, the expected number of boundary crossings is ${\displaystyle 2p}$. But each line that intersects ${\displaystyle K}$ intersects its opaque set, so the expected number of intersections with the opaque set is at least ${\displaystyle p}$, which is at least half that for ${\displaystyle K}$. By the Crofton formula, the lengths of the boundary and barrier have the same proportion as these expected numbers.

This lower bound of ${\displaystyle |\partial K|/2}$ on the length of an opaque set cannot be improved to have a larger constant factor than 1/2, because there exist examples of convex sets that have opaque sets whose length is close to this lower bound. In particular, for very long thin rectangles, one long side and two short sides form a barrier, with total length that can be made arbitrarily close to half the perimeter. Therefore, among lower bounds that consider only the perimeter of the coverage region, the bound of ${\displaystyle |\partial K|/2}$ is best possible. However, getting closer to ${\displaystyle |\partial K|/2}$ in this way involves considering a sequence of shapes rather than just a single shape, because for any convex set ${\displaystyle K}$ that is not a triangle, there exists a ${\displaystyle \delta }$ such that all opaque sets have length at least ${\displaystyle |\partial K|/2+\delta }$.

Specific shapes

For a triangle, as for any convex polygon, the shortest connected opaque set is its minimum Steiner tree. In the case of a triangle, this tree can be described explicitly: if the widest angle of the triangle is ${\displaystyle 2\pi /3}$ (120°) or more, it uses the two shortest edges of the triangle, and otherwise it consists of three line segments from the vertices to the Fermat point of the triangle. However, without assuming connectivity, the optimality of the Steiner tree has not been demonstrated. Izumi has proven a small improvement to the perimeter-halving lower bound for the equilateral triangle.

For a unit square, the perimeter is 4, the perimeter minus the longest edge is 3, and the length of the minimum Steiner tree is ${\displaystyle 1+{\sqrt {3}}\approx 2.732}$. However, a shorter, disconnected opaque forest is known, with length ${\displaystyle {\sqrt {2}}+{\tfrac {1}{2}}{\sqrt {6}}\approx 2.639}$. It consists of the minimum Steiner tree of three of the square's vertices, together with a line segment connecting the fourth vertex to the center. Ross Honsberger credits its discovery to Maurice Poirier, a Canadian schoolteacher, but it was already described in 1962 and 1964 by Jones. It is known to be optimal among forests with only two components, and has been conjectured to be the best possible more generally, but this remains unproven. The perimeter-halving lower bound of 2 for the square, already proven by Jones, can be improved slightly, to ${\displaystyle 2.00002}$, for any barrier that consists of at most countably many rectifiable curves, improving similar previous bounds that constrained the barrier to be placed only near to the given square.

The case of the unit circle was described in a 1995 Scientific American column by Ian Stewart, with a solution of length ${\displaystyle 2+\pi }$, optimal for a single curve or connected barrier but not for an opaque forest with multiple curves. Vance Faber and Jan Mycielski credit this single-curve solution to Menachem Magidor in 1974. By 1980, E. Makai had already provided a better three-component solution, with length approximately ${\displaystyle 4.7998}$, rediscovered by John Day in a followup to Stewart's column. The unknown length of the optimal solution has been called the beam detection constant.

Algorithms

Two published algorithms claim to generate the optimal opaque forest for arbitrary polygons, based on the idea that the optimal solution has a special structure: a Steiner tree for one triangle in a triangulation of the polygon, and a segment in each remaining triangle from one vertex to the opposite side, of length equal to the height of the triangle. This structure matches the conjectured structure of the optimal solution for a square. Although the optimal triangulation for a solution of this form is not part of the input to these algorithms, it can be found by the algorithms in polynomial time using dynamic programming. However, these algorithms do not correctly solve the problem for all polygons, because some polygons have shorter solutions with a different structure than the ones they find. In particular, for a long thin rectangle, the minimum Steiner tree of all four vertices is shorter than the triangulation-based solution that these algorithms find. No known algorithm has been guaranteed to find a correct solution to the problem, regardless of its running time.

Despite this setback, the shortest single-curve barrier of a convex polygon, which is the traveling salesperson path of its vertices, can be computed exactly in polynomial time for convex polygons by a dynamic programming algorithm, in models of computation for which sums of radicals can be computed exactly. There has also been more successful study of approximation algorithms for the problem, and for determining the coverage of a given barrier.

Approximation

By the general bounds for opaque forest length in terms of perimeter, the perimeter of a convex set approximates its shortest opaque forest to within a factor of two in length. In two papers, Dumitrescu, Jiang, Pach, and Tóth provide several linear-time approximation algorithms for the shortest opaque set for convex polygons, with better approximation ratios than two:

• For general opaque sets, they provide an algorithm whose approximation ratio is at most $${\displaystyle {\frac {1}{2}}+{\frac {2+{\sqrt {2}}}{\pi }}\approx 1.5868.}$$ The general idea of the algorithm is to construct a "bow and arrow" like barrier from the minimum-perimeter bounding box of the input, consisting of a polygonal chain stretched around the polygon from one corner of the bounding box to the opposite corner, together with a line segment connecting a third corner of the bounding box to the diagonal of the box.
• For opaque sets consisting of a single arc, they provide an algorithm whose approximation ratio is at most $${\displaystyle {\frac {\pi +5}{\pi +2}}\approx 1.5835.}$$ The resulting barrier is defined by a supporting line of the input shape. The input projects perpendicularly onto an interval of this line, and the barrier connects the two endpoints of this interval by a U-shaped curve stretched tight around the input, like the optimal connected barrier for a circle. The algorithm uses rotating calipers to find the supporting line for which the length of the resulting barrier is minimized.
• For connected opaque sets, they provide an algorithm whose approximation ratio is at most ${\displaystyle 1.5716}$. This method combines the single-arc barrier with special treatment for shapes that are close to an equilateral triangle, for which the Steiner tree of the triangle is a shorter connected barrier.
• For interior barriers, they provide an algorithm whose approximation ratio is at most ${\displaystyle 1.7168}$. The idea is to use a generalization suggested by Shermer of the structure of the incorrect earlier algorithms (a Steiner tree on a subset of the points, together with height segments for a triangulation of the remaining input), with a fast approximation for the Steiner tree part of the approximation.

Additionally, because the shortest connected interior barrier of a convex polygon is given by the minimum Steiner tree, it has a polynomial-time approximation scheme.

Coverage

The region covered by a given forest can be determined as follows:

• Find the convex hull of each connected component of the forest.
• For each vertex ${\displaystyle p}$ of the hull, sweep a line circularly around ${\displaystyle p}$, subdividing the plane into wedges within which the sweep line crosses one of the hulls and wedges within which the sweep line crosses the plane without obstruction. The union of the covered wedges forms a set ${\displaystyle C_{p}}$.
• Find the intersection of all of the sets ${\displaystyle C_{p}}$. This intersection is the coverage of the forest.

If the input consists of ${\displaystyle n}$ line segments forming ${\displaystyle m}$ connected components, then each of the ${\displaystyle n}$ sets ${\displaystyle C_{p}}$ consists of at most ${\displaystyle 2m}$ wedges. It follows that the combinatorial complexity of the coverage region, and the time to construct it, is ${\displaystyle O(m^{2}n^{2})}$ as expressed in big O notation.

Although optimal in the worst case for inputs whose coverage region has combinatorial complexity matching this bound, this algorithm can be improved heuristically in practice by a preprocessing phase that merges overlapping pairs of hulls until all remaining hulls are disjoint, in time ${\displaystyle O(n\log ^{2}n)}$. If this reduces the input to a single hull, the more expensive sweeping and intersecting algorithm need not be run: in this case the hull is the coverage region.

Curve-free opaque sets

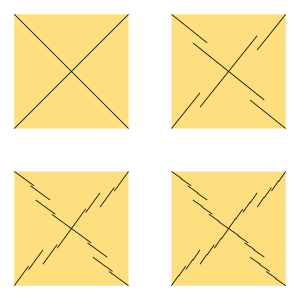
Mazurkiewicz (1916) showed that it is possible for an opaque set to avoid containing any nontrivial curves and still have finite total length. A simplified construction of Bagemihl (1959), shown in the figure, produces an example for the unit square. The construction begins with line segments that form an opaque set with an additional property: the segments of negative slope block all lines of non-negative slope, while the segments of positive slope block all lines of non-positive slope. In the figure, the initial segments with this property are four disjoint segments along the diagonals of the square. Then, it repeatedly subdivides these segments while maintaining this property. At each level of the construction, each line segment is split by a small gap near its midpoint into two line segments, with slope of the same sign, that together block all lines of the opposite sign that were blocked by the original line segment. The limit set of this construction is a Cantor space that, like all intermediate stages of the construction, is an opaque set for the square. With quickly decreasing gap sizes, the construction produces a set whose Hausdorff dimension is one, and whose one-dimensional Hausdorff measure (a notion of length suitable for such sets) is finite.

The distance sets of the boundary of a square, or of the four-segment shortest known opaque set for the square, both contain all distances in the interval from 0 to ${\displaystyle {\sqrt {2}}}$. However, by using similar fractal constructions, it is also possible to find fractal opaque sets whose distance sets omit infinitely many of the distances in this interval, or that (assuming the continuum hypothesis) form a set of measure zero.

History

Opaque sets were originally studied by Stefan Mazurkiewicz in 1916. Other early works on opaque sets include the papers of H. M. Sen Gupta and N. C. Basu Mazumdar in 1955, and by Frederick Bagemihl in 1959, but these are primarily about the distance sets and topological properties of barriers rather than about minimizing their length. In a postscript to his paper, Bagemihl asked for the minimum length of an interior barrier for the square, and subsequent work has largely focused on versions of the problem involving length minimization. They have been repeatedly posed, with multiple colorful formulations: digging a trench of as short a length as possible to find a straight buried telephone cable, trying to find a nearby straight road while lost in a forest, swimming to a straight shoreline while lost at sea, efficiently painting walls to render a glass house opaque, etc.

The problem has also been generalized to sets that block all geodesics on a Riemannian manifold, or that block lines through sets in higher-dimensions. In three dimensions, the corresponding question asks for a collection of surfaces of minimum total area that blocks all visibility across a solid. However, for some solids, such as a ball, it is not clear whether such a collection exists, or whether instead the area has an infimum that cannot be attained.

See also

• Bellman's lost-in-a-forest problem
• Euclid's orchard

References

1. ^ Mazurkiewicz, Stefan (1916), "Sur un ensemble fermé, punctiforme, qui rencontre toute droite passant par un certain domaine", Prace Mat.-Fiz. (in Polish and French), 27: 11–16
2. ^ Bagemihl, F. (1959), "Some opaque subsets of a square", Michigan Mathematical Journal, 6 (2): 99–103, doi:10.1307/mmj/1028998183, MR 0105657
3. ^ Provan, J. Scott; Brazil, Marcus; Thomas, Doreen; Weng, Jia F. (2012), Minimum opaque covers for polygonal regions, arXiv:1210.8139, Bibcode:2012arXiv1210.8139P
4. ^ Dumitrescu, Adrian; Jiang, Minghui; Pach, János (2014), "Opaque sets", Algorithmica, 69 (2): 315–334, arXiv:1005.2218, doi:10.1007/s00453-012-9735-2, MR 3183418, S2CID 13884553
5. ^ Kawohl, Bernd (1997), "The opaque square and the opaque circle", in Bandle, Catherine; Everitt, William N.; Losonczi, Laszlo; Walter, Wolfgang (eds.), General inequalities, 7 (Oberwolfach, 1995), International Series of Numerical Mathematics, vol. 123, Basel: Birkhäuser, pp. 339–346, doi:10.1007/978-3-0348-8942-1_27, ISBN 978-3-0348-9837-9, MR 1457290
6. ^ Dumitrescu, Adrian; Jiang, Minghui (2014), "The opaque square", Proc. 30th Annual Symposium on Computational Geometry (SoCG'14), New York: Association for Computing Machinery, pp. 529–538, arXiv:1311.3323, doi:10.1145/2582112.2582113, ISBN 978-1-4503-2594-3, MR 3382335, S2CID 207211457
7. ^ Kawamura, Akitoshi; Moriyama, Sonoko; Otachi, Yota; Pach, János (2019), "A lower bound on opaque sets" (PDF), Computational Geometry, 80: 13–22, doi:10.1016/j.comgeo.2019.01.002, MR 3945133
8. ^ Faber, V.; Mycielski, J. (1986), "The shortest curve that meets all the lines that meet a convex body", The American Mathematical Monthly, 93 (10): 796–801, doi:10.2307/2322935, JSTOR 2322935, MR 0867106
9. Nahin, Paul J. (2021), "Chapter 7: The Modern Age Begins", When Least Is Best: How Mathematicians Discovered Many Clever Ways to Make Things as Small (or as Large) as Possible, Princeton University Press, pp. 279–330, doi:10.2307/j.ctv19qmf43.12, JSTOR j.ctv19qmf43.12
10. Izumi, Taisuke (2016), "Improving the lower bound on opaque sets for equilateral triangle", Discrete Applied Mathematics, 213: 130–138, doi:10.1016/j.dam.2016.05.006, MR 3544574
11. Honsberger, Ross (1978), "Problem 12: An opaque square", Mathematical Morsels, The Dolciani Mathematical Expositions, vol. 3, New York: Mathematical Association of America, pp. 22–25, ISBN 978-0-88385-303-0, MR 0490615
12. ^ Jones, Robert Edward Douglas (1962), "Chapter 4: Opaque subsets of a square", Linear measure and opaque sets, Retrospective Theses and Dissertations, vol. 2058, Iowa State University, pp. 36–45, doi:10.31274/rtd-180813-2223
13. ^ Jones, R. E. D. (1964), "Opaque sets of degree ${\displaystyle \alpha }$", The American Mathematical Monthly, 71: 535–537, doi:10.2307/2312596, JSTOR 2312596, MR 0164898
14. Kawohl, Bernd (2000), "Some nonconvex shape optimization problems", Optimal shape design (Tróia, 1998), Lecture Notes in Mathematics, vol. 1740, Berlin: Springer, pp. 7–46, doi:10.1007/BFb0106741, ISBN 978-3-540-67971-4, MR 1804684
15. Stewart, Ian (September 1995), "The great drain robbery", Scientific American, 273 (3): 206–207, Bibcode:1995SciAm.273c.206S, doi:10.1038/scientificamerican0995-206, JSTOR 24981805
16. Eggleston, H. G. (1982), "The maximal inradius of the convex cover of a plane connected set of given length", Proceedings of the London Mathematical Society, Third Series, 45 (3): 456–478, doi:10.1112/plms/s3-45.3.456, MR 0675417
17. ^ Joris, H. (1980), "Le chasseur perdu dans la forêt", Elemente der Mathematik (in French), 35 (1): 1–14, MR 0559167; translated into English by Steven Finch, arXiv:1910.00615
18. Makai, E. Jr. (1980), "On a dual of Tarski's plank problem", 2nd Colloquium on Discrete Geometry, Inst. Math. Univ. Salzburg, pp. 127–132, Zbl 459.52005
19. Stewart, Ian (February 1996), "Feedback", Scientific American, 274 (2): 125, JSTOR 24989406
20. Finch, Steven R. (2003), "8.11 Beam detection constant", Mathematical Constants, Encyclopedia of Mathematics and its Applications, Cambridge University Press, pp. 515–519, ISBN 978-0-521-81805-6
21. Akman, Varol (1987), "An algorithm for determining an opaque minimal forest of a convex polygon", Information Processing Letters, 24 (3): 193–198, doi:10.1016/0020-0190(87)90185-2, MR 0882227, S2CID 37582183
22. Dublish, Pratul (1988), "An ${\displaystyle O(n^{3})}$ algorithm for finding the minimal opaque forest of a convex polygon", Information Processing Letters, 29 (5): 275–276, doi:10.1016/0020-0190(88)90122-6, MR 0981078
23. ^ Shermer, Thomas (1991), "A counterexample to the algorithms for determining opaque minimal forests", Information Processing Letters, 40 (1): 41–42, doi:10.1016/S0020-0190(05)80008-0, MR 1134007
24. ^ Dumitrescu, Adrian; Jiang, Minghui; Tóth, Csaba D. (2015), "Computing opaque interior barriers à la Shermer", SIAM Journal on Discrete Mathematics, 29 (3): 1372–1386, doi:10.1137/14098805X, hdl:10211.3/198469, MR 3376125
25. Beingessner, Alexis; Smid, Michiel (2012), "Computing the coverage of an opaque forest" (PDF), Proc. 24th Canadian Conference on Computational Geometry (CCCG'12), pp. 95–100
26. Barba, Luis; Beingessner, Alexis; Bose, Prosenjit; Smid, Michiel (2013), "Computing covers of plane forests" (PDF), Proc. 25th Canadian Conference on Computational Geometry (CCCG'13)
27. Sen Gupta, H. M.; Basu Mazumdar, N. C. (1955), "A note on certain plane sets of points", Bulletin of the Calcutta Mathematical Society, 47: 199–201, MR 0080287
28. Smart, J. R. (April 1966), "Searching for mathematical Talent in Wisconsin, II", The American Mathematical Monthly, 73 (4): 401–409, doi:10.2307/2315418, JSTOR 2315418; see Problem set 4, problem 5, p. 405
29. Croft, H. T. (1969), "Curves intersecting certain sets of great-circles on the sphere", Journal of the London Mathematical Society, Second Series, 1: 461–469, doi:10.1112/jlms/s2-1.1.461, MR 0247601
30. Asimov, Daniel; Gerver, Joseph L. (2008), "Minimum opaque manifolds", Geometriae Dedicata, 133: 67–82, doi:10.1007/s10711-008-9234-4, MR 2390069, S2CID 122556952
31. Brakke, Kenneth A. (1992), "The opaque cube problem", The American Mathematical Monthly, 99 (9): 866–871, doi:10.2307/2324127, JSTOR 2324127, MR 1191707

• Discrete geometry
• Visibility