Misplaced Pages

Evanescent field

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
(Redirected from Optical coupling) Type of field where the net flow of electromagnetic energy is zero "Evanesce" redirects here. For the album by Anatomy of a Ghost, see Evanesce (album).

Schematic representation of a surface wave (surface plasmon polariton) propagating along a metal-dielectric interface. The fields away from the surface die off exponentially (right hand graph) and those fields are thus described as evanescent in the z direction

In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source (oscillating charges and currents). Even when there is a propagating electromagnetic wave produced (e.g., by a transmitting antenna), one can still identify as an evanescent field the component of the electric or magnetic field that cannot be attributed to the propagating wave observed at a distance of many wavelengths (such as the far field of a transmitting antenna).

A hallmark of an evanescent field is that there is no net energy flow in that region. Since the net flow of electromagnetic energy is given by the average Poynting vector, this means that the Poynting vector in these regions, as averaged over a complete oscillation cycle, is zero.

Use of the term

In many cases one cannot simply say that a field is or is not "evanescent" – having the Poynting vector average to zero in some direction (or all directions). In most cases where they exist, evanescent fields are simply thought of and referred to the same as all other electric or magnetic fields involved, without any special recognition of those fields' evanescence. The term's use is mostly limited to distinguishing a part of a field or solution in those cases where one might only expect the fields of a propagating wave.

For instance, in the illustration at the top of the article, energy is indeed carried in the horizontal direction. However, in the vertical direction, the field strength drops off exponentially with increasing distance above the surface. This leaves most of the field concentrated in a thin boundary layer very close to the interface; for that reason, it is referred to as a surface wave. However, despite energy flowing horizontally, along the vertical there is no net propagation of energy away from (or toward) the surface, so that one could properly describe the field as being "evanescent in the vertical direction". This is one example of the context dependence of the term.

Everyday electronic devices and electrical appliances are surrounded by large fields which are evanescent; their operation involves alternating voltages (producing an electric field between them) and alternating currents (producing a magnetic field around them) which are expected to only carry power along internal wires, but not to the outsides of the devices. Even though the term "evanescent" is not mentioned in this ordinary context, the appliances' designers still may be concerned with maintaining evanescence, in order to prevent or limit production of a propagating electromagnetic wave, which would lead to radiation loss, since a propagating wave "steals" its power from the circuitry or donates unwanted interference.

The term "evanescent field" does arise in various contexts where a propagating electromagnetic wave is involved (even if confined). The term then differentiates electromagnetic field components that accompany the propagating wave, but which do not themselves propagate. In other, similar cases, where a propagating electromagnetic wave would normally be expected (such as light refracted at the interface between glass and air), the term is invoked to describe that part of the field where the wave is suppressed (such as light traveling through glass, impinging on a glass-to-air interface but beyond the critical angle).

Although all electromagnetic fields are classically governed according to Maxwell's equations, different technologies or problems have certain types of expected solutions, and when the primary solutions involve wave propagation the term evanescent is frequently applied to field components or solutions which do not share that property.

For instance, the propagation constant of a hollow metal waveguide is a strong function of frequency (a dispersion relation). Below a certain frequency (the cut-off frequency) the propagation constant becomes an imaginary number. A solution to the wave equation having an imaginary wavenumber does not propagate as a wave but falls off exponentially, so the field excited at that lower frequency is considered evanescent. It can also be simply said that propagation is "disallowed" for that frequency.

The formal solution to the wave equation can describe modes having an identical form, but the change of the propagation constant from real to imaginary as the frequency drops below the cut-off frequency totally changes the physical nature of the result. The solution may be described as a "cut-off mode" or an "evanescent mode"; while a different author will just state that no such mode exists. Since the evanescent field corresponding to the mode was computed as a solution to the wave equation, it is often discussed as being an "evanescent wave" even though its properties (such as carrying no energy) are inconsistent with the definition of wave.

Although this article concentrates on electromagnetics, the term evanescent is used similarly in fields such as acoustics and quantum mechanics, where the wave equation arises from the physics involved. In these cases, solutions to the wave equation resulting in imaginary propagation constants are likewise called "evanescent", and have the essential property that no net energy is transferred, even though there is a non-zero field.

Evanescent wave applications

In optics and acoustics, evanescent waves are formed when waves traveling in a medium undergo total internal reflection at its boundary because they strike it at an angle greater than the critical angle. The physical explanation for the existence of the evanescent wave is that the electric and magnetic fields (or pressure gradients, in the case of acoustical waves) cannot be discontinuous at a boundary, as would be the case if there was no evanescent wave field. In quantum mechanics, the physical explanation is exactly analogous—the Schrödinger wave-function representing particle motion normal to the boundary cannot be discontinuous at the boundary.

Electromagnetic evanescent waves have been used to exert optical radiation pressure on small particles to trap them for experimentation, or to cool them to very low temperatures, and to illuminate very small objects such as biological cells or single protein and DNA molecules for microscopy (as in the total internal reflection fluorescence microscope). The evanescent wave from an optical fiber can be used in a gas sensor, and evanescent waves figure in the infrared spectroscopy technique known as attenuated total reflectance.

In electrical engineering, evanescent waves are found in the near-field region within one third of a wavelength of any radio antenna. During normal operation, an antenna emits electromagnetic fields into the surrounding nearfield region, and a portion of the field energy is reabsorbed, while the remainder is radiated as EM waves.

Recently, a graphene-based Bragg grating (one-dimensional photonic crystal) has been fabricated and demonstrated its competence for excitation of surface electromagnetic waves in the periodic structure using a prism coupling technique.

In quantum mechanics, the evanescent-wave solutions of the Schrödinger equation give rise to the phenomenon of wave-mechanical tunneling.

In microscopy, systems that capture the information contained in evanescent waves can be used to create super-resolution images. Matter radiates both propagating and evanescent electromagnetic waves. Conventional optical systems capture only the information in the propagating waves and hence are subject to the diffraction limit. Systems that capture the information contained in evanescent waves, such as the superlens and near field scanning optical microscopy, can overcome the diffraction limit; however these systems are then limited by the system's ability to accurately capture the evanescent waves. The limitation on their resolution is given by

k ∝ 1 d ln ⁡ 1 δ , {\displaystyle k\propto {\frac {1}{d}}\ln {\frac {1}{\delta }},}

where k {\displaystyle k} is the maximal wave vector that can be resolved, d {\displaystyle d} is the distance between the object and the sensor, and δ {\displaystyle \delta } is a measure of the quality of the sensor.

More generally, practical applications of evanescent waves can be classified as (1) those in which the energy associated with the wave is used to excite some other phenomenon within the region of space where the original traveling wave becomes evanescent (for example, as in the total internal reflection fluorescence microscope) or (2) those in which the evanescent wave couples two media in which traveling waves are allowed, and hence permits the transfer of energy or a particle between the media (depending on the wave equation in use), even though no traveling-wave solutions are allowed in the region of space between the two media. An example of this is wave-mechanical tunnelling, and is known generally as evanescent wave coupling.

Total internal reflection of light

Further information: Total internal reflection § Evanescent wave
Total internal reflection
Representation of a (top) refracted incident wave and (bottom) evanescent wave at an interface in red (reflected waves omitted).

For example, consider total internal reflection in two dimensions, with the interface between the media lying on the x axis, the normal along y, and the polarization along z. One might expect that for angles leading to total internal reflection, the solution would consist of an incident wave and a reflected wave, with no transmitted wave at all, but there is no such solution that obeys Maxwell's equations. Maxwell's equations in a dielectric medium impose a boundary condition of continuity for the components of the fields E||, H||, Dy, and By. For the polarization considered in this example, the conditions on E|| and By are satisfied if the reflected wave has the same amplitude as the incident one, because these components of the incident and reflected waves superimpose destructively. Their Hx components, however, superimpose constructively, so there can be no solution without a non-vanishing transmitted wave. The transmitted wave cannot, however, be a sinusoidal wave, since it would then transport energy away from the boundary, but since the incident and reflected waves have equal energy, this would violate conservation of energy. We therefore conclude that the transmitted wave must be a non-vanishing solution to Maxwell's equations that is not a traveling wave, and the only such solutions in a dielectric are those that decay exponentially: evanescent waves.

Mathematically, evanescent waves can be characterized by a wave vector where one or more of the vector's components has an imaginary value. Because the vector has imaginary components, it may have a magnitude that is less than its real components.

For the plane of incidence as the x y {\displaystyle xy} plane at z = 0 {\displaystyle z=0} and the interface of the two mediums as the x z {\displaystyle xz} plane at y = 0 {\displaystyle y=0} , the wave vector of the transmitted wave has the form

k t   =   k y y ^ + k x x ^ {\displaystyle \mathbf {k_{t}} \ =\ k_{y}{\hat {\mathbf {y} }}+k_{x}{\hat {\mathbf {x} }}}

with k x = k t sin ⁡ θ t {\displaystyle k_{x}=k_{t}\sin \theta _{t}} and k y = k t cos ⁡ θ t {\displaystyle k_{y}=k_{t}\cos \theta _{t}} , where k t {\displaystyle k_{t}} is the magnitude of the wave vector of the transmitted wave (so the wavenumber), θ t {\displaystyle \theta _{t}} is the angle of refraction, and x ^ {\displaystyle {\hat {\mathbf {x} }}} and y ^ {\displaystyle {\hat {\mathbf {y} }}} are the unit vectors along the x {\displaystyle x} axis direction and the y {\displaystyle y} axis direction respectively.

By using the Snell's law n i sin ⁡ θ i = n t sin ⁡ θ t {\displaystyle n_{i}\sin \theta _{i}=n_{t}\sin \theta _{t}} where n i {\displaystyle n_{i}} , n t {\displaystyle n_{t}} , and θ i {\displaystyle \theta _{i}} are the refractive index of the medium where the incident wave and the reflected wave exist, the refractive index of the medium where the transmitted wave exists, and the angle of incidence respectively,

k y = k t cos ⁡ θ t = ± k t ( 1 − sin 2 ⁡ θ i n t i 2 ) 1 / 2 {\displaystyle k_{y}=k_{t}\cos \theta _{t}=\pm k_{t}\left(1-{\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}\right)^{1/2}} .

with n t i = n t n i {\textstyle n_{ti}={\frac {n_{t}}{n_{i}}}} .

If a part of the condition of the total internal reflection as sin ⁡ θ i > sin ⁡ θ c = n t i {\displaystyle \sin \theta _{i}>\sin \theta _{c}=n_{ti}} , is satisfied, then

k y = ± i k t ( sin 2 ⁡ θ i n t i 2 − 1 ) 1 / 2 = ± i α {\displaystyle k_{y}=\pm ik_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}=\pm i\alpha } .

If the polarization is perpendicular to the plane of incidence (along the z {\displaystyle z} direction), then the electric field of any of the waves (incident, reflected, or transmitted) can be expressed as

E ( r , t ) = Re ⁡ { E ( r ) e i ω t } z ^ {\displaystyle \mathbf {E} (\mathbf {r} ,t)=\operatorname {Re} \left\{E(\mathbf {r} )e^{i\omega t}\right\}\mathbf {\hat {z}} }

where z ^ {\displaystyle \mathbf {\hat {z}} } is the unit vector in the z {\displaystyle z} axis direction.

By assuming plane waves as E ( r ) = E 0 e − i k ⋅ r {\displaystyle E(\mathbf {r} )=E_{0}e^{-i\mathbf {k} \cdot \mathbf {r} }} , and substituting the transmitted wave vector k t {\displaystyle \mathbf {k_{t}} } into k {\displaystyle \mathbf {k} } , we find for the transmitted wave:

E ( r ) = E o e − i ( − i α y + β x ) = E o e − α y − i β x {\displaystyle E(\mathbf {r} )=E_{o}e^{-i(-i\alpha y+\beta x)}=E_{o}e^{-\alpha y-i\beta x}}

where α = k t ( sin 2 ⁡ θ i n t i 2 − 1 ) 1 / 2 {\textstyle \alpha =k_{t}\left({\frac {\sin ^{2}\theta _{i}}{n_{ti}^{2}}}-1\right)^{1/2}} is the attenuation constant, and β = k x {\displaystyle \beta =k_{x}} is the phase constant. + i α {\displaystyle +i\alpha } is ignored since it does not physically make sense (the wave amplification along y the direction in this case).

Evanescent-wave coupling

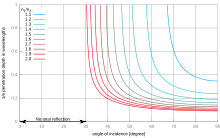
Plot of 1/e-penetration depth of the evanescent wave against angle of incidence in units of wavelength for different refraction indices.

Especially in optics, evanescent-wave coupling refers to the coupling between two waves due to physical overlap of what would otherwise be described as the evanescent fields corresponding to the propagating waves.

One classical example is frustrated total internal reflection (FTIR) in which the evanescent field very close (see graph) to the surface of a dense medium at which a wave normally undergoes total internal reflection overlaps another dense medium in the vicinity. This disrupts the totality of the reflection, diverting some power into the second medium.

Coupling between two optical waveguides may be effected by placing the fiber cores close together so that the evanescent field generated by one element excites a wave in the other fiber. This is used to produce fiber-optic splitters and in fiber tapping. At radio (and even optical) frequencies, such a device is called a directional coupler. The device is usually called a power divider in the case of microwave transmission and modulation.

Evanescent-wave coupling is synonymous with near field interaction in electromagnetic field theory. Depending on the nature of the source element, the evanescent field involved is either predominantly electric (capacitive) or magnetic (inductive), unlike (propagating) waves in the far field where these components are connected (identical phase, in the ratio of the impedance of free space). The evanescent wave coupling takes place in the non-radiative field near each medium and as such is always associated with matter; i.e., with the induced currents and charges within a partially reflecting surface. In quantum mechanics the wave function interaction may be discussed in terms of particles and described as quantum tunneling.

Applications

Evanescent wave coupling is commonly used in photonic and nanophotonic devices as waveguide sensors or couplers (see e.g., prism coupler).

Evanescent wave coupling is used to excite, for example, dielectric microsphere resonators.

Evanescent coupling, as near field interaction, is one of the concerns in electromagnetic compatibility.

Coupling of optical fibers without loss for fiber tapping.

Evanescent wave coupling plays a major role in the theoretical explanation of extraordinary optical transmission.

Evanescent wave coupling is used in powering devices wirelessly.

A total internal reflection fluorescence microscope uses the evanescent wave produced by total internal reflection to excite fluorophores close to a surface. This is useful when surface properties of biological samples need to be studied.

See also

Notes

  1. Or, expressing the fields E and H as phasors, the complex Poynting vector S = E × H ∗ {\displaystyle \mathbf {S} =\mathbf {E} \times \mathbf {H} ^{*}} has a zero real part.

References

  1. Takayama, O.; Bogdanov, A.A.; Lavrinenko, A.V. (2017). "Photonic surface waves on metamaterial interfaces". Journal of Physics: Condensed Matter. 29 (46): 463001. Bibcode:2017JPCM...29T3001T. doi:10.1088/1361-648X/aa8bdd. PMID 29053474. S2CID 1528860.
  2. IEEE Standard Dictionary of Electrical and Electronics Terms. New York, NY: The Institute of Electrical and Electronics Engineers. 1992. p. 458. ISBN 978-1-55937-240-4. IEEE STD 100-1992.
  3. Jackson, John David (1999). Classical Electrodynamics (3rd ed.). John-Wiley. ISBN 047130932X.
  4. Tineke Thio (2006). "A Bright Future for Subwavelength Light Sources". American Scientist. 94 (1): 40–47. doi:10.1511/2006.1.40.
  5. Marston, Philip L.; Matula, T.J. (May 2002). "Scattering of acoustic evanescent waves". Journal of the Acoustical Society of America. 111 (5): 2378. Bibcode:2002ASAJ..111.2378M. doi:10.1121/1.4778056.
  6. Sreekanth, Kandammathe Valiyaveedu; Zeng, Shuwen; Shang, Jingzhi; Yong, Ken-Tye; Yu, Ting (2012). "Excitation of surface electromagnetic waves in a graphene-based Bragg grating". Scientific Reports. 2: 737. Bibcode:2012NatSR...2E.737S. doi:10.1038/srep00737. PMC 3471096. PMID 23071901.
  7. Neice, A., "Methods and Limitations of Subwavelength Imaging", Advances in Imaging and Electron Physics, Vol. 163, July 2010.
  8. Hecht, Eugene (2017). Optics (5th Global ed.). Pearson. pp. 135–137. ISBN 978-1-292-09693-3.
  9. Zeng, Shuwen; Yu, Xia; Law, Wing-Cheung; Zhang, Yating; Hu, Rui; Dinh, Xuan-Quyen; Ho, Ho-Pui; Yong, Ken-Tye (2013). "Size dependence of Au NP-enhanced surface plasmon resonance based on differential phase measurement". Sensors and Actuators B: Chemical. 176: 1128–1133. Bibcode:2013SeAcB.176.1128Z. doi:10.1016/j.snb.2012.09.073.
  10. Lova, Paola; Manfredi, Giovanni; Comoretto, Davide (2018). "Advances in Functional Solution Processed Planar 1D Photonic Crystals". Advanced Optical Materials. 6 (24): 1800730. doi:10.1002/adom.201800730. hdl:11567/928329. ISSN 2195-1071.
  11. Fan, Zhiyuan; Zhan, Li; Hu, Xiao; Xia, Yuxing (2008). "Critical process of extraordinary optical transmission through periodic subwavelength hole array: Hole-assisted evanescent-field coupling". Optics Communications. 281 (21): 5467. Bibcode:2008OptCo.281.5467F. doi:10.1016/j.optcom.2008.07.077.
  12. Karalis, Aristeidis; J.D. Joannopoulos; Marin Soljačić (February 2007). "Efficient wireless non-radiative mid-range energy transfer". Annals of Physics. 323 (1): 34. arXiv:physics/0611063. Bibcode:2008AnPhy.323...34K. doi:10.1016/j.aop.2007.04.017. S2CID 1887505.
  13. "'Evanescent coupling' could power gadgets wirelessly", Celeste Biever, NewScientist.com, 15 November 2006
  14. Wireless energy could power consumer, industrial electronics – MIT press release
  15. Axelrod, D. (1 April 1981). "Cell-substrate contacts illuminated by total internal reflection fluorescence". The Journal of Cell Biology. 89 (1): 141–145. doi:10.1083/jcb.89.1.141. PMC 2111781. PMID 7014571.

External links

Categories: