Misplaced Pages

Osipkov–Merritt models (named for Leonid Osipkov and David Merritt) are mathematical representations of spherical stellar systems (galaxies, star clusters, globular clusters etc.). The Osipkov–Merritt formula generates a one-parameter family of phase-space distribution functions that reproduce a specified density profile (representing stars) in a specified gravitational potential (in which the stars move). The density and potential need not be self-consistently related. A free parameter adjusts the degree of velocity anisotropy, from isotropic to completely radial motions. The method is a generalization of Eddington's formula for constructing isotropic spherical models.

The method was derived independently by its two eponymous discoverers. The latter derivation includes two additional families of models (Type IIa, b) with tangentially anisotropic motions.

Derivation

According to Jeans's theorem, the phase-space density of stars f must be expressible in terms of the isolating integrals of motion, which in a spherical stellar system are the energy E and the angular momentum J. The Osipkov-Merritt ansatz is

${\displaystyle f=f(Q)=f(E+J^{2}/2r_{a}^{2})}$

where r_a, the "anisotropy radius", is a free parameter. This ansatz implies that f is constant on spheroids in velocity space since

${\displaystyle 2Q=v_{r}^{2}+(1+r^{2}/r_{a}^{2})v_{t}^{2}+2\Phi (r)}$

where v_r, v_t are velocity components parallel and perpendicular to the radius vector r and Φ(r) is the gravitational potential.

The density ρ is the integral over velocities of f:

${\displaystyle \rho (r)=2\pi \int \int f(E,J)v_{t}dv_{t}dv_{r}}$

which can be written

${\displaystyle \rho (r)={2\pi \over r^{2}}\int _{\Phi }^{0}dQf(Q)\int _{0}^{2r^{2}(Q-\Phi )/(1+r^{2}/r_{a}^{2})}dJ^{2}\left^{-1/2}}$

or

${\displaystyle \rho (r)={4\pi \over 1+r^{2}/r_{a}^{2}}\int _{\Phi }^{0}dQ{\sqrt {2(Q-\Phi )}}f(Q).}$

This equation has the form of an Abel integral equation and can be inverted to give f in terms of ρ:

${\displaystyle f(Q)={{\sqrt {2}} \over 4\pi ^{2}}{d \over dQ}\int _{Q}^{0}{d\Phi \over {\sqrt {\Phi -Q}}}{d\rho ^{'} \over d\Phi },\ \ \ \ \ \rho ^{'}(\Phi )=\left\rho \left.}$

Properties

Following a derivation similar to the one above, the velocity dispersions in an Osipkov–Merritt model satisfy

${\displaystyle {\sigma _{r}^{2} \over \sigma _{t}^{2}}=1+{r^{2} \over r_{a}^{2}}.}$

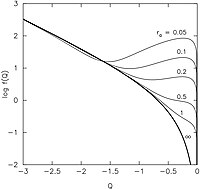
The motions are nearly radial (${\displaystyle \sigma _{r}\gg \sigma _{t}}$) for ${\displaystyle r\gg r_{a}}$ and nearly isotropic (${\displaystyle \sigma _{r}\approx \sigma _{t}}$) for ${\displaystyle r\ll r_{a}}$. This is a desirable feature, since stellar systems that form via gravitational collapse have isotropic cores and radially-anisotropic envelopes.

If r_a is assigned too small a value, f may be negative for some Q. This is a consequence of the fact that spherical mass models can not always be reproduced by purely radial orbits. Since the number of stars on an orbit can not be negative, values of r_a that generate negative f's are unphysical. This result can be used to constrain the maximum degree of anisotropy of spherical galaxy models.

In his 1985 paper, Merritt defined two additional families of models ("Type II") that have isotropic cores and tangentially anisotropic envelopes. Both families assume

${\displaystyle f=f(E-J^{2}/2r_{a}^{2})}$.

In Type IIa models, the orbits become completely circular at r=r_a and remain so at all larger radii. In Type IIb models, stars beyond r_a move on orbits of various eccentricities, although the motion is always biased toward circular. In both families, the tangential velocity dispersion undergoes a jump as r increases past r_a.

C. M. Carollo et al. (1995) derive many observable properties of Type I Osipkov–Merritt models.

Applications

Typical applications of Osipkov–Merritt models include:

• Modelling of star clusters, galaxies, dark matter halos and galaxy clusters
• Constructing anisotropic galaxy models for studies of dynamical instabilities

See also

• Stellar dynamics

References

1. Eddington, A. (1916), The distribution of stars in globular clusters, Mon. Not. R. Astron. Soc., 76, 572
2. Osipkov, L. P. (1979), Spherical systems of gravitating bodies with an ellipsoidal velocity distribution, Pis'ma v Astron. Zhur., 5, 77
3. ^ Merritt, D. (1985), Spherical stellar systems with spheroidal velocity distributions, Astron. J., 90, 1027
4. van Albada, T. (1983), Dissipationless galaxy formation and the R to the 1/4-power law, Mon. Not. R. Astron. Soc., 201, 939
5. Carollo, C. M. et al. (1995), Velocity profiles of Osipkov-Merritt models, Mon. Not. R. Astron. Soc., 276, 1131
6. Lupton, R. et al. (1989), The internal velocity dispersions of three young star clusters in the Large Magellanic Cloud, Astrophys. J., 347, 201
7. Nolthenius, R. and Ford, H. (1987), The mass and halo dispersion profile of M32, Astrophys. J., 305, 600
8. Sotnikova, N. Ya. and Rodionov, S. A. (2008), Anisotropic Models of Dark Halos, Astron. Lett., 34, 664-674
9. Lokas, E. and Mamon, G. A. (2001), Properties of spherical galaxies and clusters with an NFW density profile, Mon. Not. R. Astron. Soc., 321, 155
10. May, A. and Binney, J. (1986), Testing the stability of stellar systems, Mon. Not. R. Astron. Soc., 221, 13
11. Saha, P. (1991), Unstable modes of a spherical stellar system, Mon. Not. R. Astron. Soc., 248, 494

• Astrophysics