Misplaced Pages

Overconstrained mechanism

Article snapshot taken from Wikipedia with creative commons attribution-sharealike license. Give it a read and then ask your questions in the chat. We can research this topic together.
Moveable linkage with zero mobility
The crank-driven elliptic trammel is an overconstrained mechanism.
Trammel of Archimedes with three sliders.

In mechanical engineering, an overconstrained mechanism is a linkage that has more degrees of freedom than is predicted by the mobility formula. The mobility formula evaluates the degree of freedom of a system of rigid bodies that results when constraints are imposed in the form of joints between the links.

If the links of the system move in three-dimensional space, then the mobility formula is

M = 6 ( N − 1 − j ) + ∑ i = 1 j f i , {\displaystyle M=6(N-1-j)+\sum _{i=1}^{j}f_{i},}

where N is the number of links in the system, j is the number of joints, and fi is the degree of freedom of the ith joint.

If the links in the system move planes parallel to a fixed plane, or in concentric spheres about a fixed point, then the mobility formula is

M = 3 ( N − 1 − j ) + ∑ i = 1 j f i . {\displaystyle M=3(N-1-j)+\sum _{i=1}^{j}f_{i}.}

If a system of links and joints has mobility M = 0 or less, yet still moves, then it is called an overconstrained mechanism.

Reason of over-constraint

The reason of over-constraint is the unique geometry of linkages in these mechanisms, which the mobility formula does not take into account. This unique geometry gives rise to "redundant constraints", i.e. when multiple joints are constraining the same degrees of freedom. These redundant constraints are the reason of the over-constraint.

For example, as shown in the figure to the right, consider a hinged door with 3 hinges. The mobility criterion for this door gives the mobility to be −1. Yet, the door moves and has a degree of freedom 1, as all its hinges have colinear axes.

Examples of over-constrained mechanisms

Multi-hinged doors and the like

A multi-hinged door is an over-constrained mechanism.

The figure on the left shows a two-hinged trunk lid. The calculated mobility for the lid relative to the car body is zero, yet it moves as its hinges (which are pin joints) have colinear axes. In this case, the second hinge is kinematically redundant.

Parallel linkage

Overconstrained parallel linkage

A well-known example of an overconstrained mechanism is the parallel linkage with multiple cranks, as seen in the running gear of steam locomotives.

Sarrus linkage

A Sarrus linkage.

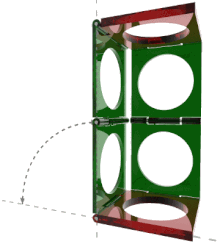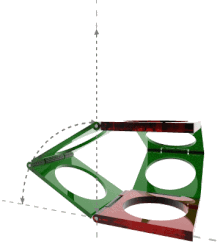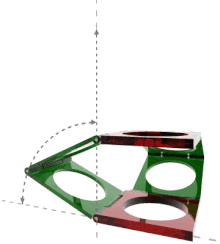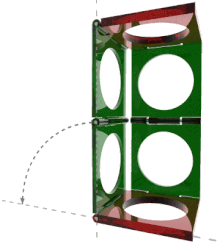
Sarrus mechanism consists of six bars connected by six hinged joints.

A general spatial linkage formed from six links and six hinged joints has mobility

M = 6 ( N − 1 − j ) + ∑ i = 1 j f i = 6 ( 6 − 1 − 6 ) + 6 = 0 , {\displaystyle M=6(N-1-j)+\sum _{i=1}^{j}f_{i}=6(6-1-6)+6=0,}

and is therefore a structure.

The Sarrus mechanism has one degree of freedom whereas the mobility formula yields M = 0, which means it has a particular set of dimensions that allow movement.

Bennett's linkage

A Bennett's linkage

Another example of an overconstrained mechanism is Bennett's linkage, invented by Geoffrey Thomas Bennett in 1903, which consists of four links connected by four revolute joints.

A general spatial linkage formed from four links and four hinged joints has mobility

M = 6 ( N − 1 − j ) + ∑ i = 1 j f i = 6 ( 4 − 1 − 4 ) + 4 = − 2 , {\displaystyle M=6(N-1-j)+\sum _{i=1}^{j}f_{i}=6(4-1-4)+4=-2,}

which is a highly constrained system.

As in the case of the Sarrus linkage, it is a particular set of dimensions that makes the Bennett linkage movable.

The dimensional constraints that makes Bennett's linkage movable are the following. Let us number the links in order that links with consecutive index are joined (first and fourth links are also joined). For the i-th link, let us denote by di and ai respectively the distance and the oriented angle of the axes of the revolute joints of the link. Bennett's linkage must satisfies the following constraints:

d 1 = d 3 , a 1 = a 3 d 2 = d 4 , a 2 = a 4 d 1 2 sin 2 ⁡ a 1 = d 2 2 sin 2 ⁡ a 2 . {\displaystyle {\begin{aligned}&d_{1}=d_{3},\quad a_{1}=a_{3}\\&d_{2}=d_{4},\quad a_{2}=a_{4}\\&{\frac {d_{1}^{2}}{\sin ^{2}a_{1}}}={\frac {d_{2}^{2}}{\sin ^{2}a_{2}}}.\end{aligned}}}

Moreover, the links are assembled in such a way that, for two links that are joined, the common perpendicular to the joint axes of the first link intersects the common perpendicular of the joint axes of the second link.

Below is an external link to an animation of a Bennett's linkage.

Watt steam engine

Watt steam engine.

James Watt employed an approximate straight line four-bar linkage to maintain a near rectilinear motion of the piston rod, thus eliminating the need of using a crosshead.

Hoberman mechanism

Same as the crank-driven elliptic trammel, Hoberman mechanisms move because of their particular geometric configurations.

Assembly of cognate linkages

Overconstrained mechanisms can be also obtained by assembling together cognate linkages; when their number is more than two, overconstrained mechanisms with negative calculated mobility will result. The companion animated GIFs show overconstrained mechanisms obtained by assembling together four-bar coupler cognates and function cognates of the Watt II type.

Animation Gallery

  • Coupler cognates of a four-bar linkage. Coupler cognates of a four-bar linkage.
  • Coupler cognates of a slider-crank linkage. Coupler cognates of a slider-crank linkage.
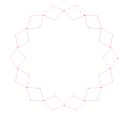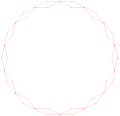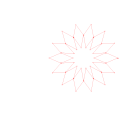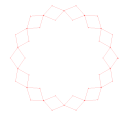  • Hoberman ring. Hoberman ring.
  • 3R-R-3R Watt II function cognates. 3R-R-3R Watt II function cognates.
  • 3R-P-3R Watt II function cognates. 3R-P-3R Watt II function cognates.

References

  1. K. J. Waldron, Overconstrained Linkage Geometry by Solution of Closure Equations---Part 1. Method of Study, Mechanism and Machine Theory, Vol. 8, pp. 94–104, 1973.
  2. Bennett, Geoffrey Thomas (December 4, 1903). "A New Mechanism". Engineering. 76: 777–778.
  3. J. M. McCarthy and G. S. Soh, Geometric Design of Linkages, 2nd Edition, Springer 2010
  4. Dai, J.S., Huang, Z., Lipkin, H., "Mobility of Overconstrained Parallel Mechanisms", Special Supplement on Spatial Mechanisms and Robot Manipulators, Transactions of the ASME: Journal of Mechanical Design, 128(1): 220–229, 2006.
  5. Simionescu, P.A.; Smith, M.R. (2000). "Applications of Watt II function generator cognates". Mechanism and Machine Theory. 35 (11): 1535–1549. doi:10.1016/S0094-114X(00)00011-2.
  6. Simionescu, P.A.; Smith, M.R. (2001). "Four- and six-bar function cognates and overconstrained mechanisms". Mechanism and Machine Theory. 36 (8): 913–924. doi:10.1016/S0094-114X(01)00031-3.
  7. Wei, G., Chen, Y. and Dai, J. S., Synthesis, "Mobility and Multifurcation of Deployable Polyhedral Mechanisms with Radially Reciprocating Motion", ASME Journal of Mechanical Design, 136(9), p.091003, 2014.

External links

Category: